Урок "Похідна та її застосування" 10 ккас

Тема уроку: «Похідна та її застосування»

Мета уроку:

 Освітня:  систематизувати знання учнів з теми;  формувати  в учнів уміння творчо застосовувати набуті знання до розв’язувати прикладних задач; ознайомити учнів із завданнями по даній темі із ЗНО; встановлення міжпредметних зв’язків  математики та інших наук.

Розвивальна: розвивати самостійну та пізнавальну діяльності учнів, вміння логічного та творчого  мислити, висловлювати  свою думку; формувати вміння вести дослідницько-пошукову роботу; критичність, логічність мислення, інтерес до предмета, інтерес до процесу навчання, застосовувати набуті знання до розв’язування вправ у стандартних та нестандартних ситуація.

Виховна: виховувати самостійність, уміння самоорганізовуватись; відповідальність, стійкість, наполегливість, взаємоповагу один до одного.

Формування ключових компетентностей:

• математична грамотність;
• екологічна грамотність і здорове життя;
• інформаційно - цифрова;
• вчитися впродовж життя.

Тип уроку:  урок застосування знань, умінь і навичок

Епіграф: «Усе що я пізнаю, я знаю, для чого це мені потрібно,  де і як я можу це знання застосувати»                      

                                                    В. Килпатрик

                         Хід уроку

І. Мотивація навчальної діяльності. Формулювання цілей та завдань уроку.

Добрий дня, шановні учні та гості. Ми раді вітати вас на нашому уроці. Те про що ми будемо говорити вже відкрито, але можливо, ви, шановні гості, з нашою допомогою щось нове відкриєте для себе. Тож бажаю всім гарного настрою та приємно провести час.

Похідна-фундаментальне поняття математики, за допомогою якого досліджують процеси і  явища в природних, соціальних і економічних науках. Тому вивченню цієї теми ми приділяємо особливу увагу.

ІІ. Актуалізація опорних  знань.

1. Не змінюючи традицій розпочнемо з перевірки домашнього завдання.

Чи виникли у Вас труднощі з прикладами? Назвіть відповідь 22, 23, 24

 

В, В, Б, Д

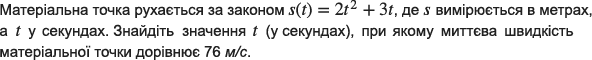
Відповідь.18,25с

2. « Бліц опитування»

 -   Дати означення похідної?

 -   У чому полягає геометричний зміст похідної?

 -   Що таке кутовий коефіцієнт прямої?  Чому він дорівнює?

 -   У чому полягає механічний зміст похідної?

 -   Як знайти найбільше та найменше значення функції на відрізку?

 -   Які правила диференціювання ви знаєте?

 

3.    Усний рахунок  «Знайди помилку»

а)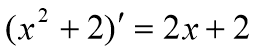

б)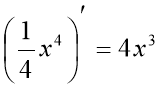

в)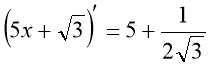   

г)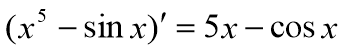

д)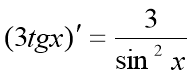

4. Робота учнів на індивідуальних картках

 

І варіант	IІ варіант
Знайти похідну: у = х 4  - 6                  2)  у = (x - 2) · x3;          у = tg x + 1.            Знайдіть похідну функції  у = sin х - cos х та обчислити її значення, якщо     x  =	Знайти похідну: у =  х 3  +   у = (х3 -2)(х-4)   у = сtg x + 5х.            Точка рухається за законом S(t) == t3 – 4t2. Знайдіть миттєву швидкість точки в момент t = 5 с (s вимірюється в метрах).
ІІІ варіант	IV варіант
Знайти похідну: у =  х 5 + +   у = (x2 - х)(х3 + x).   у = у = sinx;        4. Точка рухається прямолінійно за законом s(t) = 2 t 3 - 3t (s — шлях в метрах, t — час в секундах). Обчисліть швидкість руху точки:  в момент t = 2 с.	Знайти похідну: у = х 7 -2-  у = x2cos x;       у =   Точка рухається за законом S(t) = t 3 + 3t2. Знайдіть миттєву швидкість точки в момент t = 2 с (s вимірюється в метрах).

 

ІІІ. Хвилинка відпочинку.

   Заздалегідь учні об’єдналися у 4 групи: «Історики», «Теоретики», «Практики»,  «Філологи». Кожна група одержала завдання: опрацювати додаткову літературу, довідники, Інтернет  та знайти у різних сферах задачі прикладного характеру, а також історичний матеріал щодо походження похідної.

VI. Сприймання і засвоєння нових знань

 

 

 

                               МАТЕРІАЛ ГРУПИ « ІСТОРИКИ»

      Нашій групі « Історики» було доручено з’ясувати,  хто із вчених і коли ввів поняття «похідної».  Опрацювавши літературу ми зв’ясували.що

відкриттю похідної та основ диференціального числення передували роботи французьких математиків П’єра Ферма (1601-1665), який у 1629 р. запропонував способи знаходження найбільших і найменших значень функцій, а також Рене Декарта (1596-1650), який розробив метод координат і основи аналітичної геометрії.

 У 1670-1671рр. англійський математик і механік Ісаак Ньютон (1643-1727) і дещо пізніше у 1673-1675 рр. німецький філософ і математик Готфрід  Вільгельм Лейбніц (1646 – 1716 ) незалежно один від одного побудували теорію диференціального числення .

І. Ньютон прийшов до поняття похідної, розв’язуючи задачі про миттєву швидкість, а Лейбніц – розглядаючи геометричну задачу про проведення дотичної до кривої.

     Термін «похідна» ввів у 1797 р. французький математик Жозеф Луї Лагранж (1736 – 1813 ). Він ввів і сучасні позначення для похідної у вигляді  y^/   та f^{/ .}  

      Велику роль у розвитку диференціального числення відіграв видатний математик, фізик, механік і астроном Леонард Ейлер, який написав підручник « Диференціальне числення» (1755 р.).

Розвиток науково-технічного прогресу, виготовлення зброї, епідемії і відкриття цілющого пеніциліну, запуск космічної ракети і створення ядерних реакторів – основою цього всього послужило диференціальне числення. Від високих досягнень  до стрімких падінь крокувала поряд похідна, кидаючи свої максимуми і мінімуми¸ похідна, яка миттєво змінила світ.

                            МАТЕРІАЛ ГРУПИ « теоретики »

Нашій групі було доручено знайти матеріал про застосування похідної в різних галузях науки та техніки. Опрацювавши літературу  ми прийшли до висновку , що значення похідної є багатогранним .

• В математиці похідна характеризує кривизну графіка функції.
•  в механіці - швидкість нерівномірного прямолінійного руху, швидкості зміни температури під час нагрівання; визначення освітленості електричної лампочки.
• в біології - швидкість розмноження колонії мікроорганізмів.
•  в економіці - вихід продукту на одиницю витрат.
•  в хімії - швидкість хімічної реакції, швидкості зростання маси кристалів.

Виявили найхарактерніші задачі:

  -    дослідження та побудова графіків функцій;

• знаходження найбільшого та найменшого значення функції на відрізку;
• розв’язування рівнянь ;
• доведення  нерівностей;

  -    розв’язування завдань з параметрами;

• наближені обчислення .

                    МАТЕРІАЛ ГРУПИ « Практики»

Наша команда працювала  під девізом « Недостатньо лише мати гарний розум, головне – це добре застосувати його».             

Ми  одержали завдання: знайти задачі, які розв’язуються за допомогою похідної в різних галузях науки. Пропонуємо  їх вашій увазі.

Біологія .  Нехай популяція кисломолочних бактерій в момент часу t (час в секундах) нараховує x(t) особин.  Формула, що виражає залежність кількості особин від часу X(t)=3000+100. Знайти швидкість росту популяції:

а) в момент часу 1 сек

б) в момент часу 60 сек.

Розв´язання:

- швидкість росту популяції

(ос\сек) -  швидкість рості популяції через 1 сек

(ос\сек) швидкість росту популяції через 60 сек

Ці бактерії є одними з небагатьох мікроорганізмів, що вважаються безпечними для споживання в їжу живими, через їх поширеність в продуктах харчування та ролі в здоровій флорі слизу травного тракту.

 

 Медицина.  Кількість людей, які під час епідемії грипу захворіють за один день обчислюється за формулою N(t)=0,003t(50-t). Знайдіть швидкість поширення епідемії.  На який день епідемія досягне максимуму, через скільки днів згасне.

Відповідь. Максимуму на 25день, згасне через 50.

 Профілактика грипу та ГРВІ

 1. Частіше мийте руки

2. Робіть вологе прибирання

3. Провітрюйте приміщення

4. Зволожуйте слизові оболонки

 

                   МАТЕРІАЛ ГРУПИ «Філологи»

 Як відомо похідну застосовують для дослідження графіків функції,

але щоб проілюструвати характерні властивості функції, можна звернутися до прислів’я, адже прислів’я – це відображення стійких закономірностей, перевірених багатолітнім досвідом народу.

 Перша жінка математик Софія Ковалевська сказала:

«Математик повинен бути поетом в душі». І, слідуючи її словами, ми пропонуємо відкрити літературну сторінку «Графіки функцій - прислів'я». Підберіть до графіків функцій, зображених на слайдах прислів'я, які розкривають суть процесів функції:

 

V. Підсумок уроку

Підсумок уроку проводиться у формі інтерактивної гри «Мікрофон».

Уявіть собі, що до вас завітав журналіст газети «Шкільні новини», який хоче написати, що нового і цікавого ви дізналися на уроці. Прохання дати відповіді на такі запитання, тримаючи в руках перехідний мікрофон.

  1.Над якою темою працювали на уроці?

  2.Що нового дізналися при вивченні даної теми?

  3. Чого навчилися, готуючи матеріал?

  4. Що складного було на уроці?

5. Чим запам’ятався урок?
6. Де зможете застосувати одержану інформацію?

 

  Оцінювання роботи учнів на уроці за картками самоконтролю

VI. Домашнє завдання: повторити таблицю похідних, №20.38, 20.58.

А тепер все відкладіть в сторону розкрийте свою ліву долоню і покладіть на неї той досвід, з яким ви прийшли сьогодні на урок. Відчуйте його значення для вас. А тепер покажіть свою праву долоню і покладіть на неї ту інформацію і той досвід, який ви здобули сьогодні. Відчуйте його цінність для вас. А тепер з'єднайте долоні, об'єднайте ці досвіди, і нехай вони допоможуть вам успішно здати ЗНО. Успіхів ВАМ!