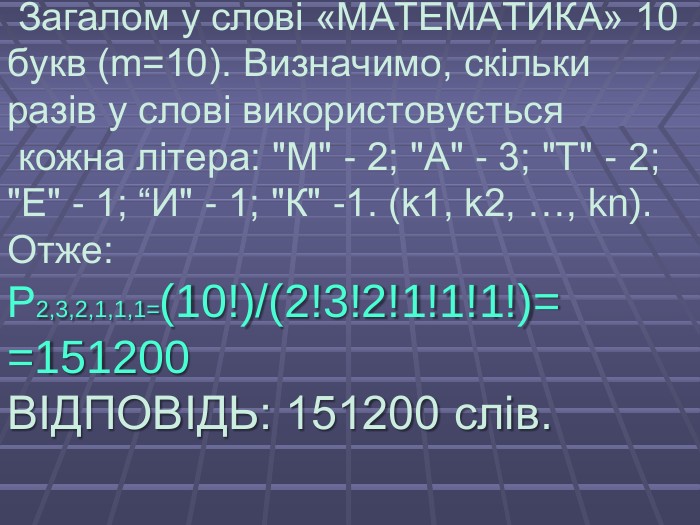
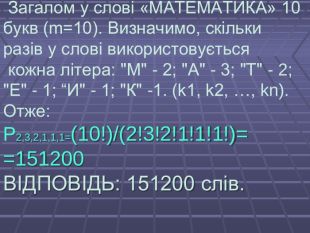
Презентація "Елементи комбінаторики. Перестановки"
Про матеріал
У Презентації подано означення, формули для розрахунку кількості перестановок та перестановок з повторенням. Є іторичні довідки. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра (академічний, профільний рівень) 11 клас (Нелін Є.П., Долгова О.Є.)
До уроку
21.1. Елементи комбінаторики Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку