Презентація "Формула Піка для обчислення площ многокутників"

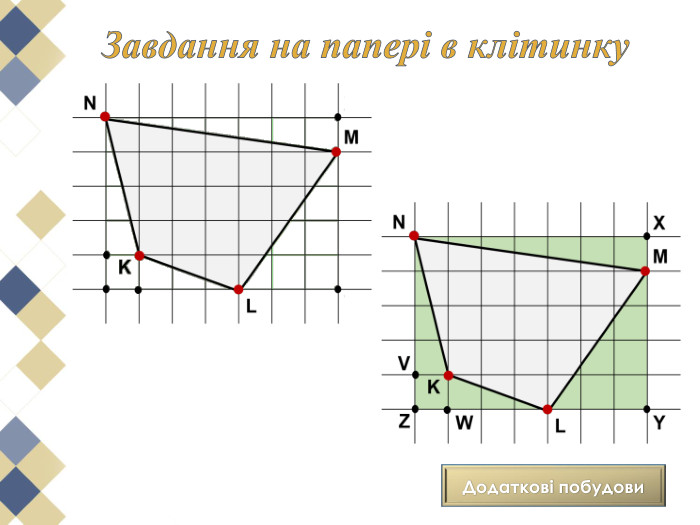
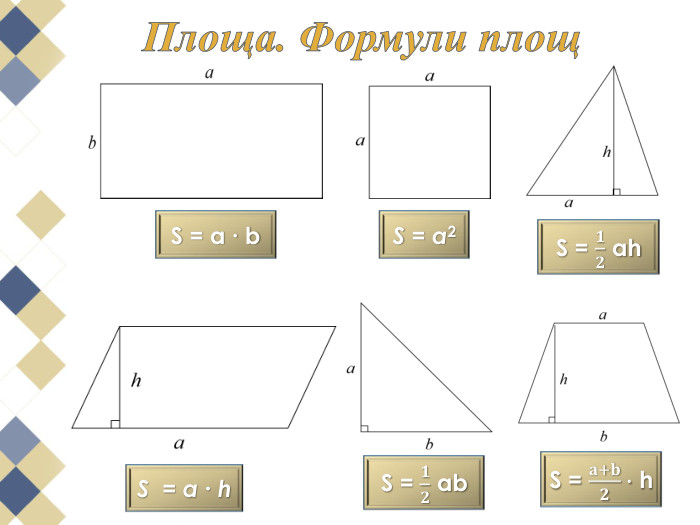
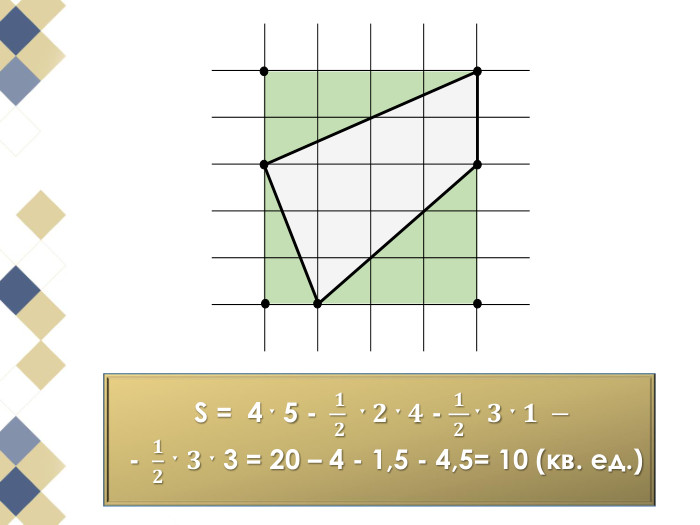
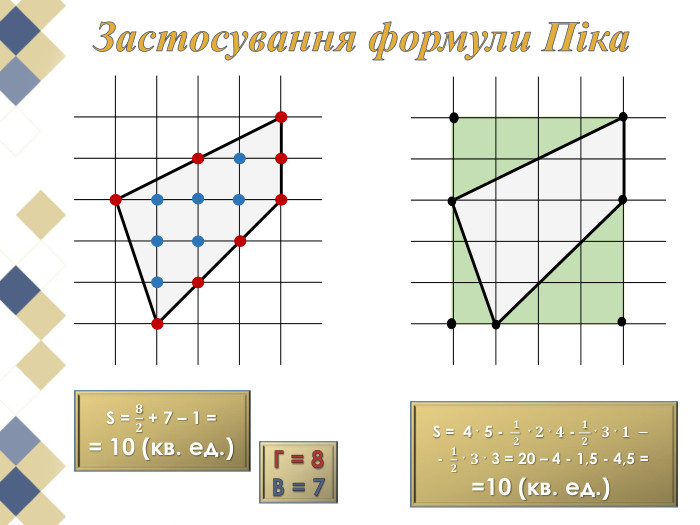
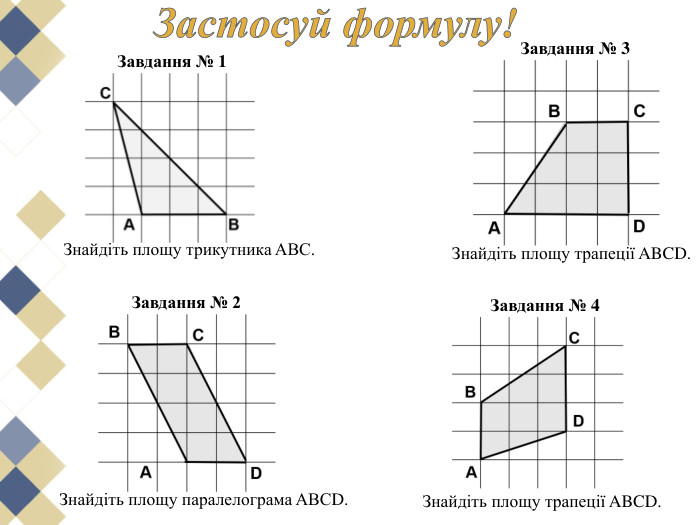
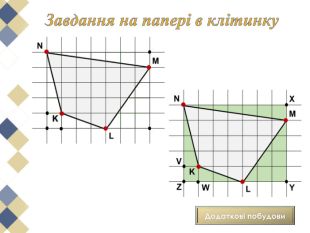
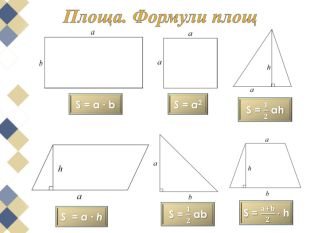
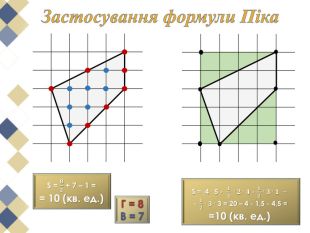
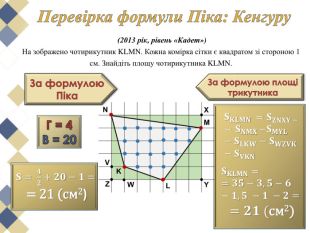
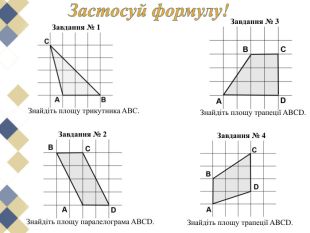
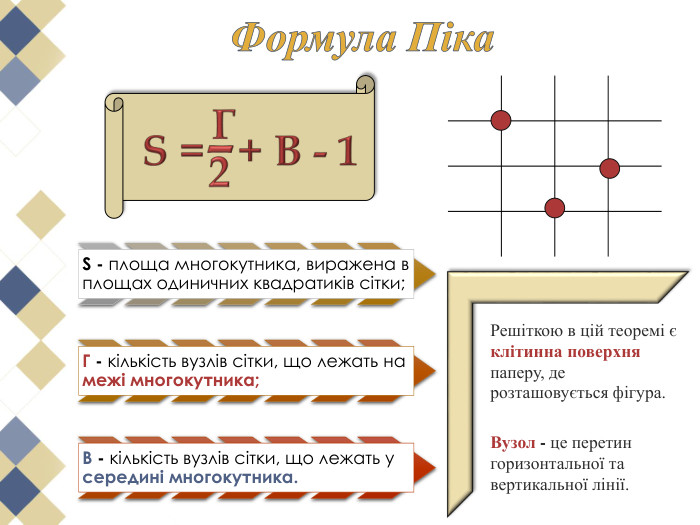
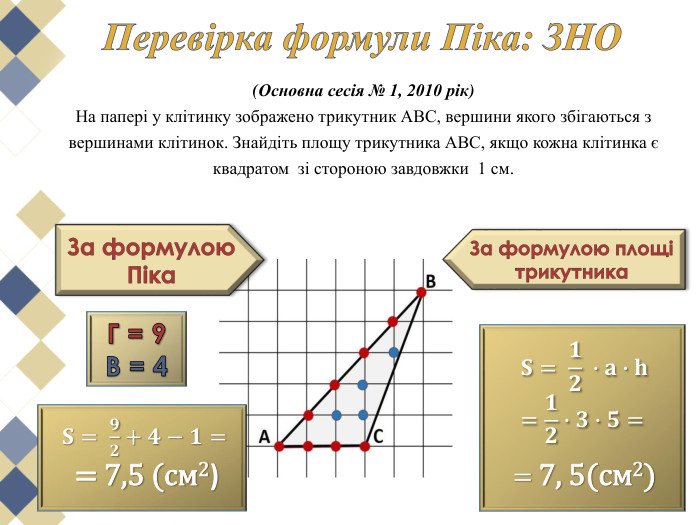
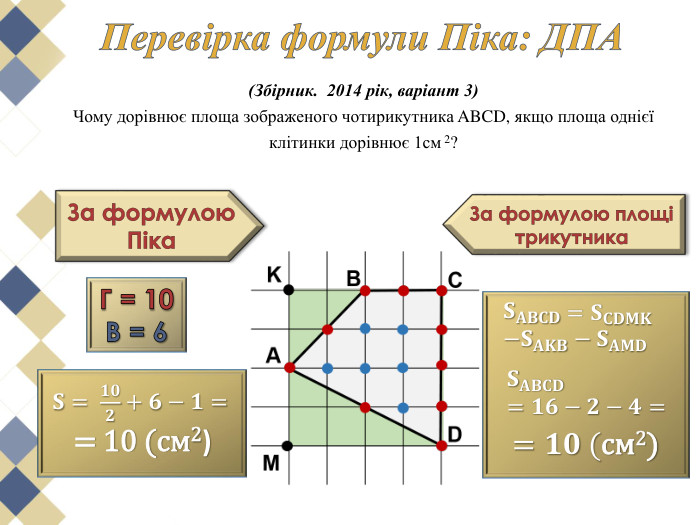
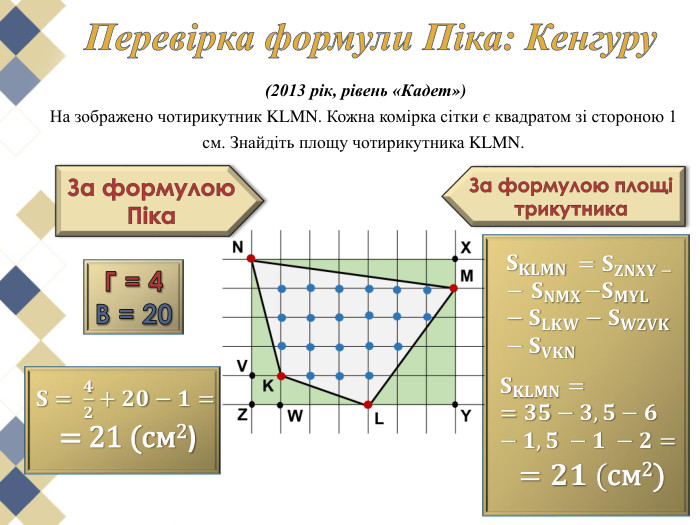
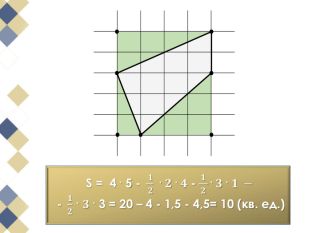
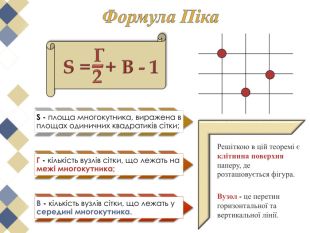
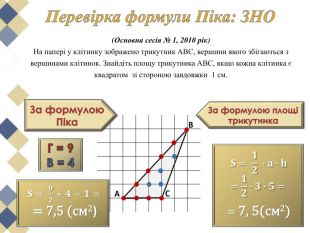
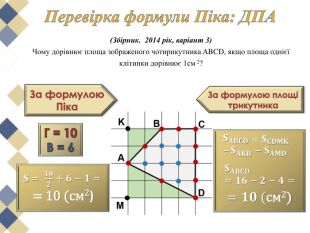
Намалюємо на папері в клітинку многокутник та спробуємо розрахувати його площу. Напевно, найпростіше розбити його на квадрати, прямокутники або прямокутні трикутники, площі яких неважко обчислити та скласти отримані результати. Використаний спосіб нескладний, але досить громіздкий. Виявляється, що є дуже проста формула, що дозволяє обчислити площі таких многокутників з вершинами у вузлах квадратної сітки. Ця чудова і проста формула називається формулою (теоремою) Піка. У чому ж краса цієї теореми? В тому, що вона проста та досить цікава.