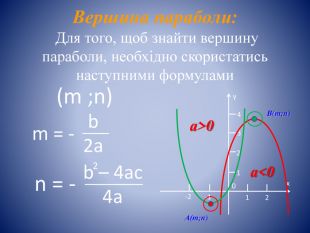
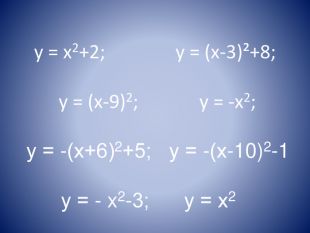Презентація к уроку "Квадратична функція"












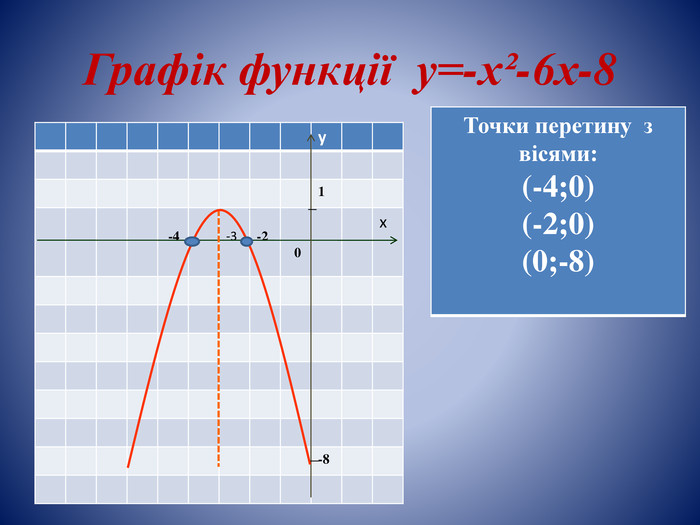
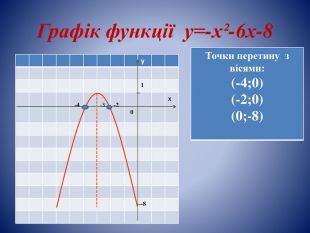
![Властивості функції:у>0 на проміжку у<0 на проміжку. Функція зростає на проміжку. Функція спадає на проміжку. Найбільше значення функції дорівнює(-4;-2)(-∞;-4);(-2;+∞)(-∞;-3][-3;+∞)1, при х=-3 Властивості функції:у>0 на проміжку у<0 на проміжку. Функція зростає на проміжку. Функція спадає на проміжку. Найбільше значення функції дорівнює(-4;-2)(-∞;-4);(-2;+∞)(-∞;-3][-3;+∞)1, при х=-3](/uploads/files/1546383/198449/214496_images/18.jpg)









![Карточка №1. При яких значеннях а функція y=ax2+5 має нулі? а) а>0; б) а≠0; в) а<0 Карточка №2 Найдіть проміжок спадання функції y = (x-2)2+2 а) (- ∞; 1,5]; б) (-∞ ; 3]; в) (-∞ ; 2) Карточка №1. При яких значеннях а функція y=ax2+5 має нулі? а) а>0; б) а≠0; в) а<0 Карточка №2 Найдіть проміжок спадання функції y = (x-2)2+2 а) (- ∞; 1,5]; б) (-∞ ; 3]; в) (-∞ ; 2)](/uploads/files/1546383/198449/214496_images/28.jpg)

![Карточка №5 Графіком квадратичної функції є парабола з вершиною в точці А(0;1), вітки направлені вгору. Задайте цю функцію формулою. а) y = -x2+1; б) y=x2-1; в) y=x2+1 . Карточка №6 Знайдіть проміжок зростання функції y = (x-2)2+2 а) (2;+ ∞); б) (-∞ ; 3]; в) (-∞ ; 2) Карточка №5 Графіком квадратичної функції є парабола з вершиною в точці А(0;1), вітки направлені вгору. Задайте цю функцію формулою. а) y = -x2+1; б) y=x2-1; в) y=x2+1 . Карточка №6 Знайдіть проміжок зростання функції y = (x-2)2+2 а) (2;+ ∞); б) (-∞ ; 3]; в) (-∞ ; 2)](/uploads/files/1546383/198449/214496_images/30.jpg)


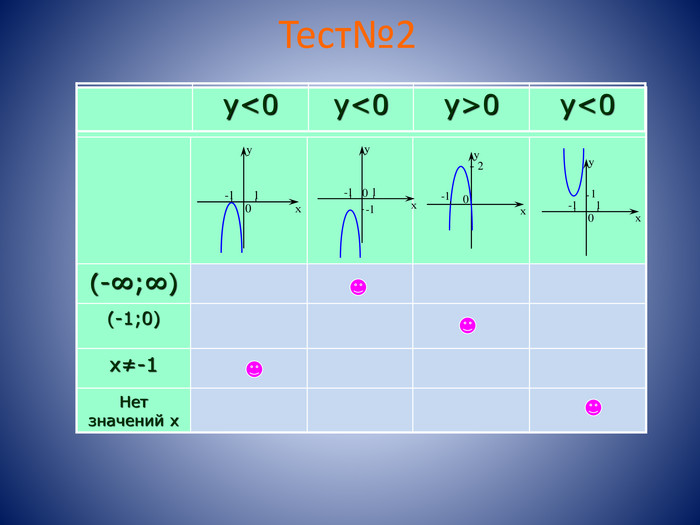

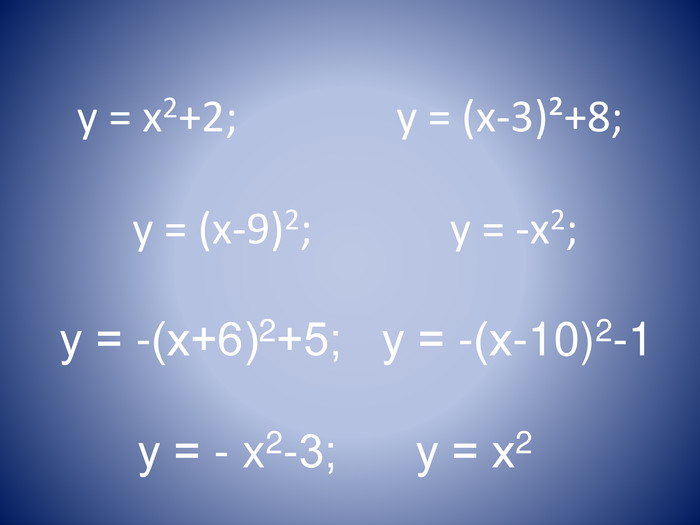



Квадратична функція, її властивості і графік. Мета: узагальнення та закріплення знань; відпрацювання навичок розв’язання тестових завдань; відпрацювання алгоритму побудови графіка квадратичної функції. Задачі: повторити властивості квадратичної функції, систематизувати знання з побудови графіка квадратичної функції.
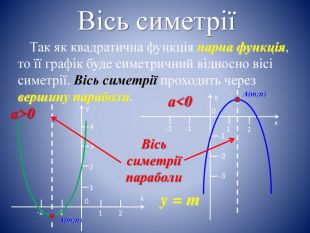
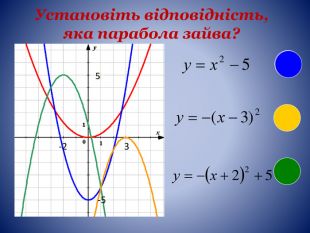
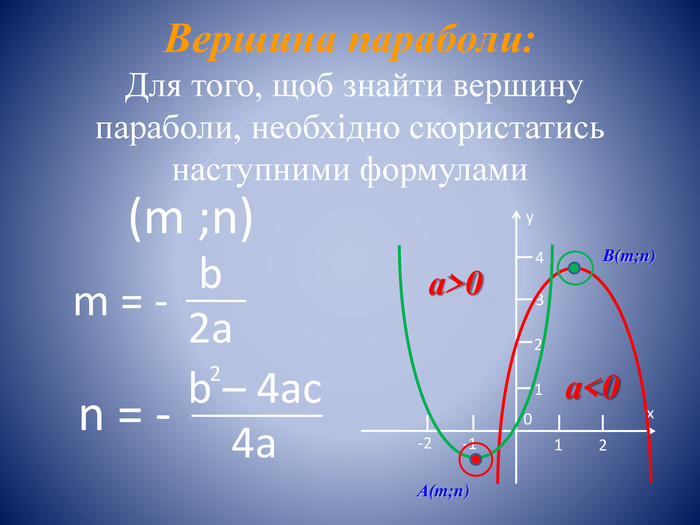
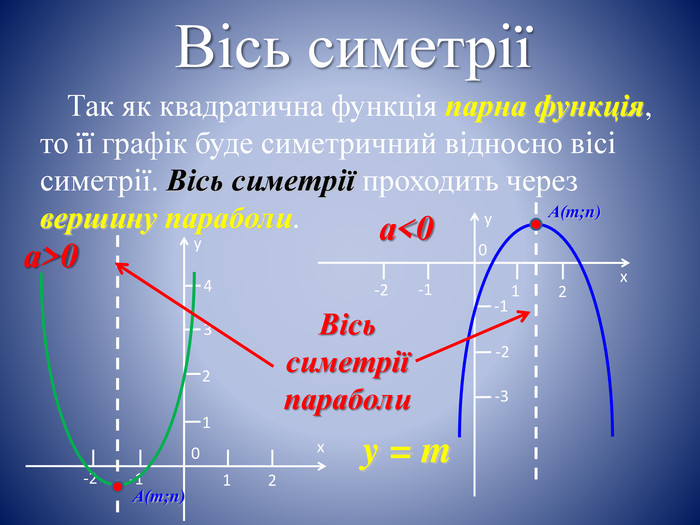
Вісь симетріїТак як квадратична функція парна функція, то її графік буде симетричний відносно вісі симетрії. Вісь симетрії проходить через вершину параболи.yх021-2-11234 А(m;n) yх021-2-1-1-2-3 А(m;n) Вісь симетрії параболиy = mа>0а<0style.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type
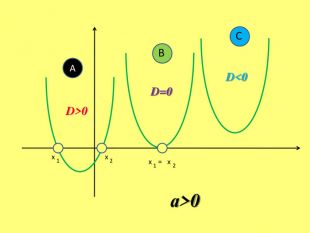
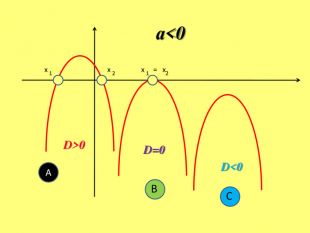
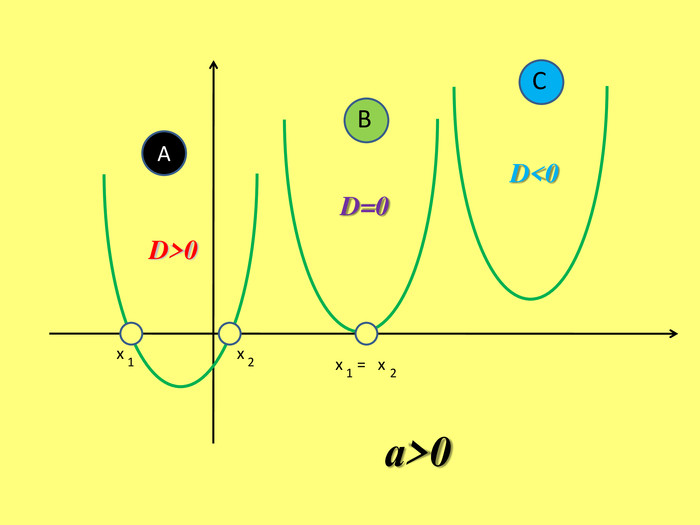
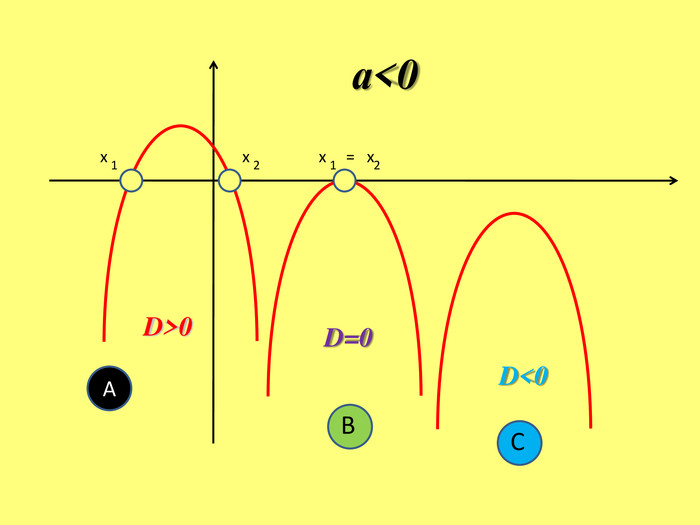
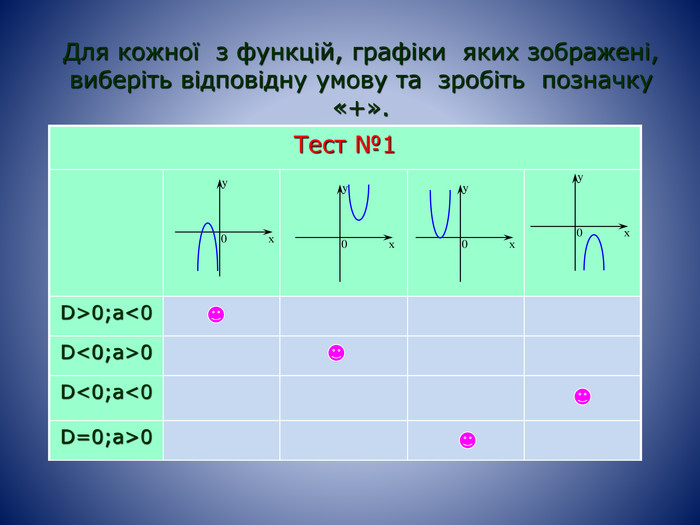
Якщо D>0 ,то ми будемо мати 2 дійсних-різних кореніх1= х2=Якщо D=0, то ми матимемо 2 дійсних-рівних кореніх1,2=графік функції тільки в одній точці перетинає вісь 0х (дотикається до вісі 0х) і точка дотику буде в вершині параболи. Якщо D<0, то дійсних коренів квадратний тричлен не матиме, графік функції не перетинає вісь 0х в жодній точці АВС
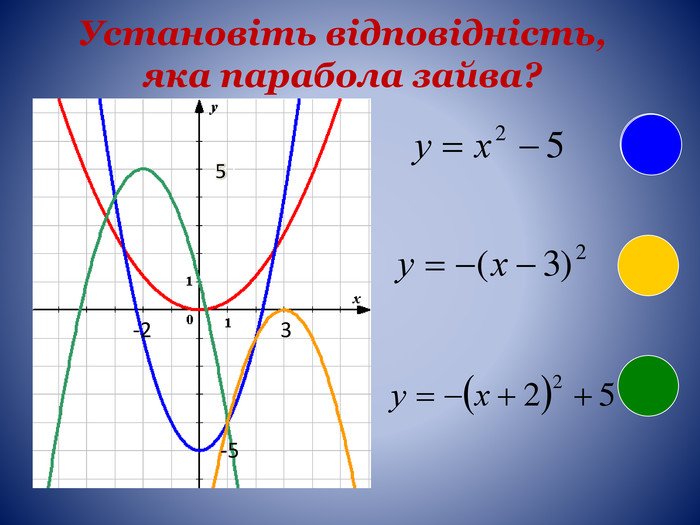
А(1;-5)Карточка №3 Записати рівняння параболи, яку отримують з параболи y=x2 зсувом вздовж вісі ОХ на 2 одиниці вліво и вздовж вісі ОУ на 1 одиницю вниз. а) y=(x-2)2-1; б) у= (x+2)2-1; в) y=(x-2)2+1 Карточка №4 Установіть, яка з точок А(1;-5), В(4;9),С(-4;11) належить графіку функції y=3(x-1)2-5


про публікацію авторської розробки
Додати розробку