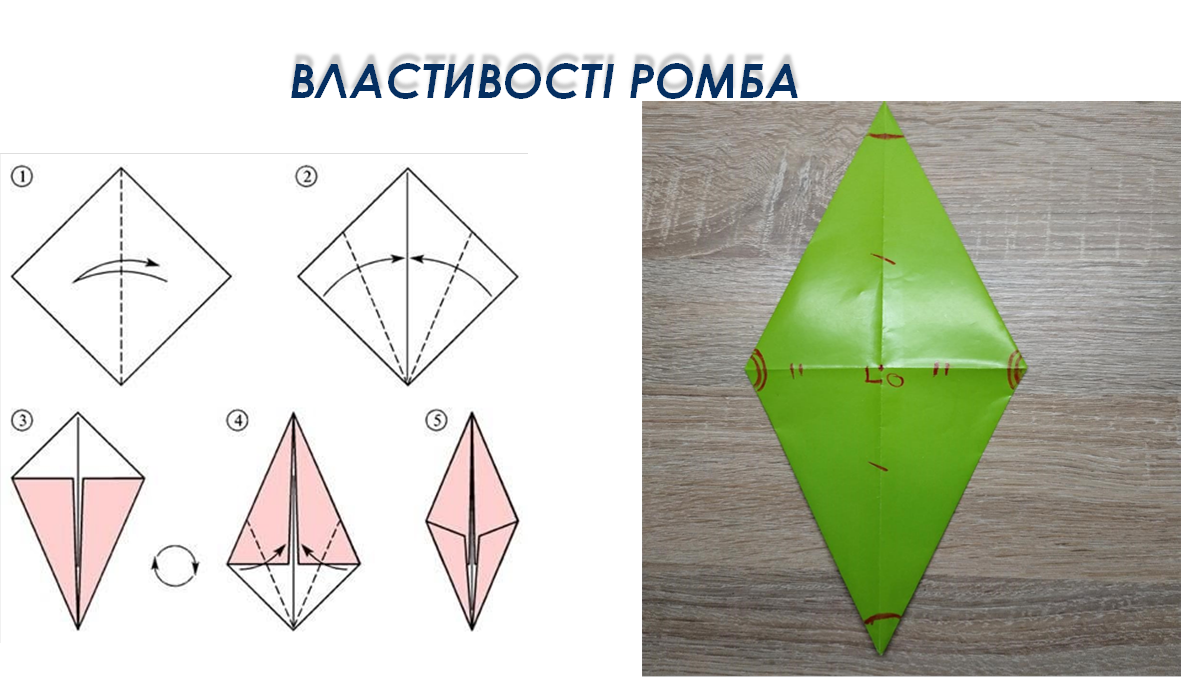
Геометрія – це світ фігур та їх властивостей: трикутників, чотирикутників, многокутників тощо. Для покращення сприйняття матеріалу учням необхідний практичний матеріал, який можна потримати в руках, тобто сприйняти властивості фігури на дотик. А що в такому випадку може стати кращим за орігамі? У такий спосіб учні не лише практично перевіряють теоретичні знання, а й самостійно отримують геометричні фігури шляхом згинання паперу.Такий підхід дозволяє показати всю красу та практичну значимість геометрії та підвищує інтерес до цієї науки.

Педагогами багатьох країн було відмічено, що робота з папером: Вчить слухати усні інструкції вчителя;

Вчить виконувати послідовні дії;

Ознайомлює на практиці з основними геометричними поняттями;

Розвиває впевненість в своїх силах і здібностях;

Допомагає розвитку перших креслярських навиків; Вчить сконцентровувати увагу;

Завдяки орігамі з’явилася можливість показати, що математика не суха наука, а поєднання краси та гармонії.

ВЛАСТИВІСТЬ ПРЯМОКУТНОГО ТРИКУТНИКА

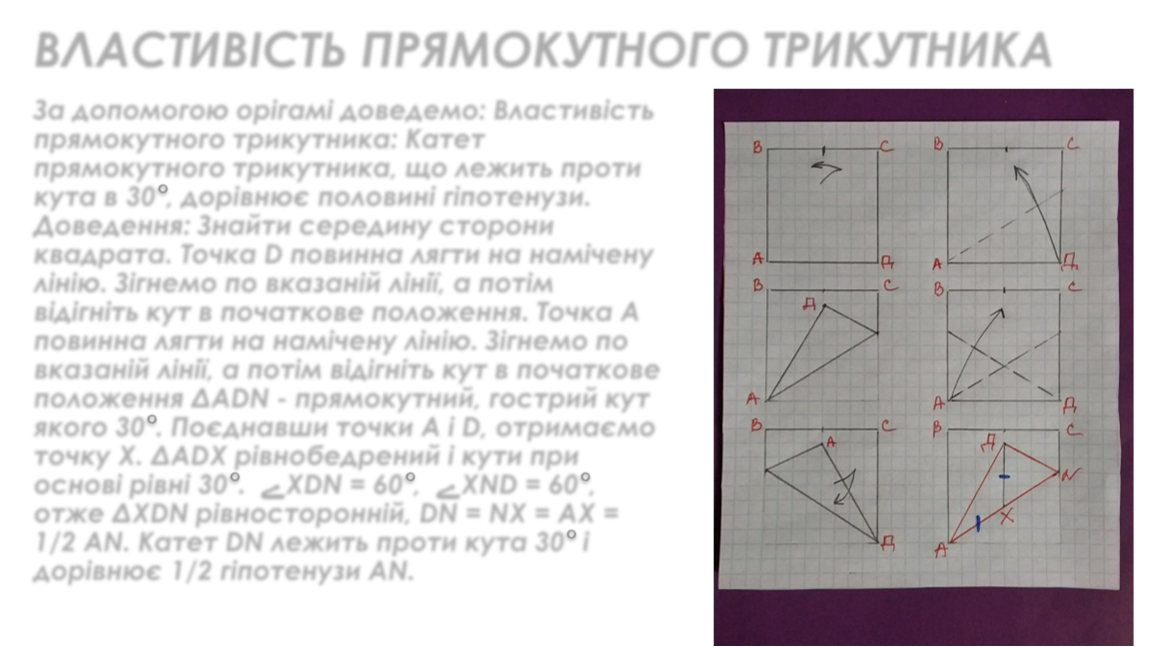За допомогою орігамі доведемо: Властивість прямокутного трикутника: Катет прямокутного трикутника, що лежить проти кута в 30°, дорівнює половині гіпотенузи. Доведення: Знайти середину сторони квадрата. Точка D повинна лягти на намічену лінію. Зігнемо по вказаній лінії, а потім відігніть кут в початкове положення. Точка А повинна лягти на намічену лінію. Зігнемо по вказаній лінії, а потім відігніть кут в початкове положення ΔADN - прямокутний, гострий кут якого 30°. Поєднавши точки A і D, отримаємо точку Х. ΔADX рівнобедрений і кути при основі рівні 30°.  ےXDN = 60°,  ےXND = 60°, отже ΔXDN рівносторонній, DN = NX = AX = 1/2 AN. Катет DN лежить проти кута 30° і дорівнює 1/2 гіпотенузи AN.

ЗАДАЧА

За допомогою орігамі розв’язуються геометричні задачі на площині. У ΔАВС проведена бісектриса ВК. Через точку К проведена пряма, яка перетинає сторону ВС в точці М так, що ВM = МК. Доведіть, що КМ // АВ. 1) Орігамі – розв’язання: Сумістим промені ВА і ВС, побудуємо бісектрису ВК.

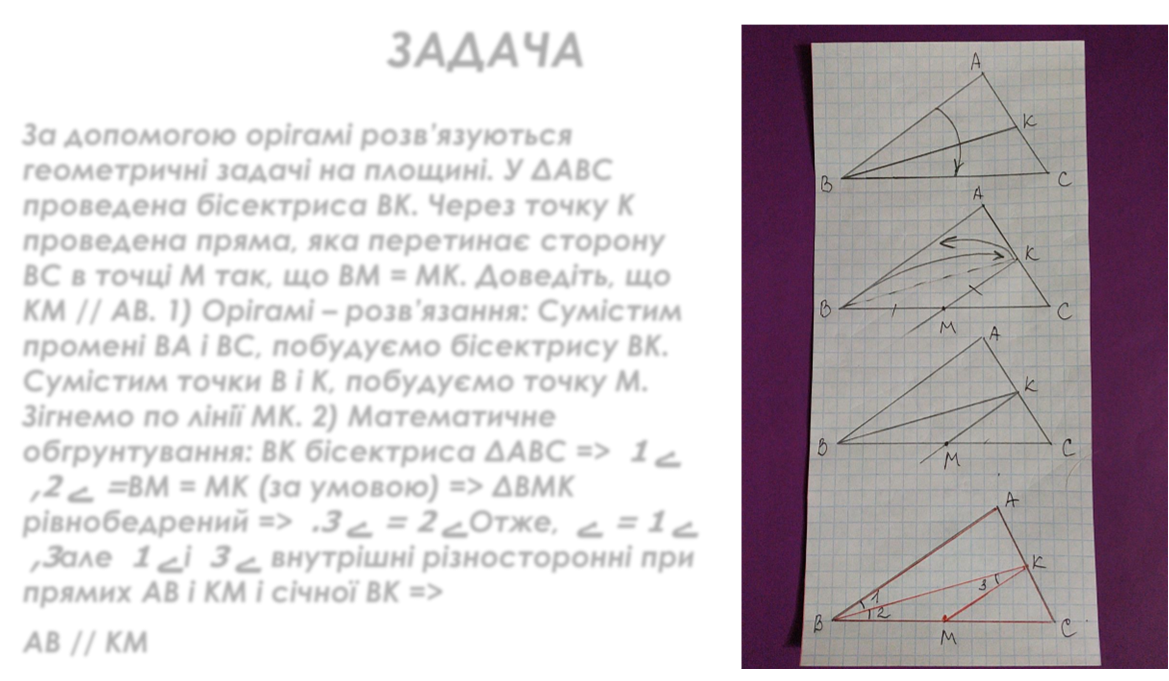Сумістим точки В і К, побудуємо точку М. Зігнемо по лінії МК. 2) Математичне обгрунтування: BK бісектриса ΔАВС => 1 ے  ,2 ے =BM = MK (за умовою) => ΔBMK рівнобедрений =>  .3 ے 2= ےОтже,  ے  1= ے ,3але 1 ےі 3 ےвнутрішні різносторонні при прямих AB і KM і січної BK =>

AB // KM

ТЕОРЕМА ПІФАГОРА

Відома теорема Піфагора - допускає багато витончених доказів. Наведемо лише один доказ, відкритий в минулому столітті Генрі Перігелом, лондонським біржовим маклером і астрономом-любителем. Побудуйте квадрати на катетах прямокутного трикутника.

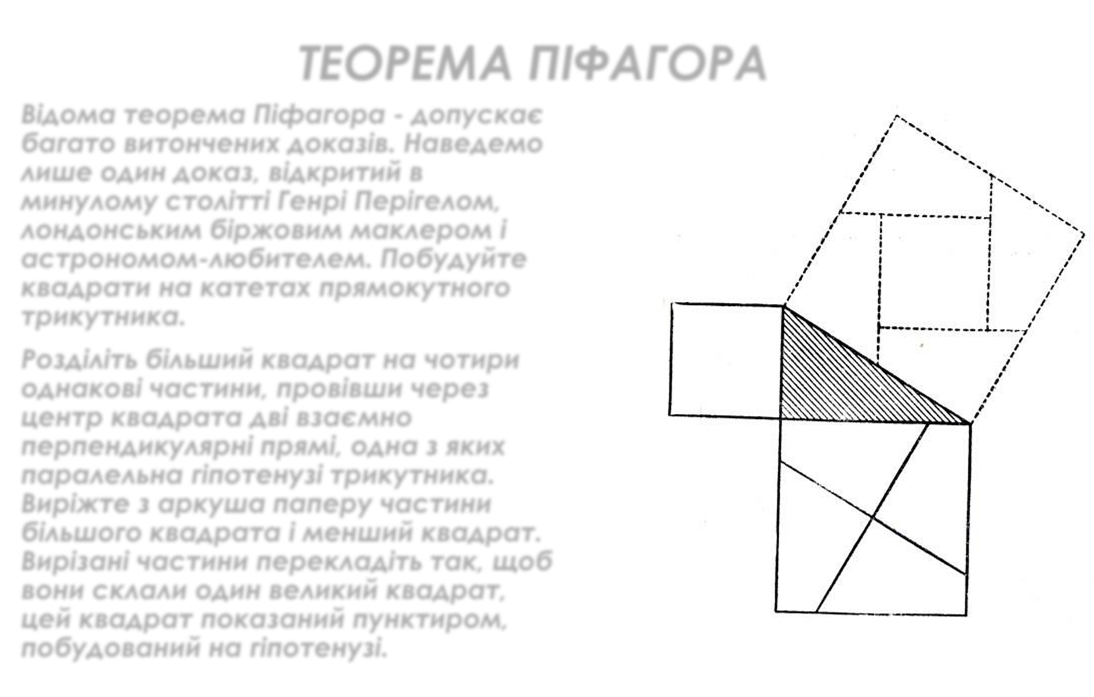Розділіть більший квадрат на чотири однакові частини, провівши через центр квадрата дві взаємно перпендикулярні прямі, одна з яких паралельна гіпотенузі трикутника. Виріжте з аркуша паперу частини більшого квадрата і менший квадрат. Вирізані частини перекладіть так, щоб вони склали один великий квадрат, цей квадрат показаний пунктиром, побудований на гіпотенузі.

На прикладах ми показали, що розв’язування геометричних задач і доведення теорем в техніці орігамі значно полегшує засвоєння

математичних понять і властивостей фігур, спонукає до подальших

Своєю роботою ми хотіли показати, що математика – це цікаво. Дійсно говорять: “Математика – цариця наук, а Геометрія – її храм”.