Презентація "Куля і сфера"
Про матеріал
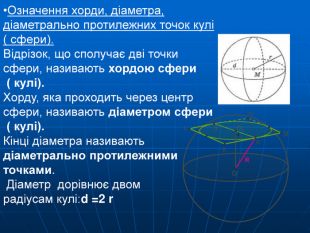
Означення кулі
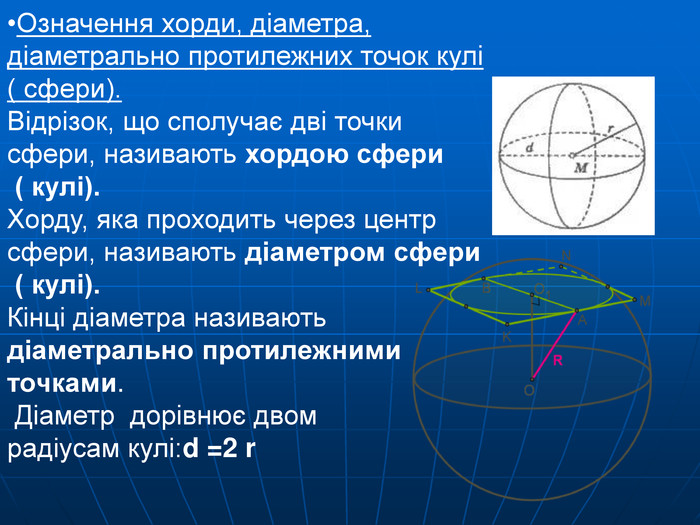
Елементи кулі (кулева поверхня, радіус, діаметр)
Означення кулі як тіла обертання
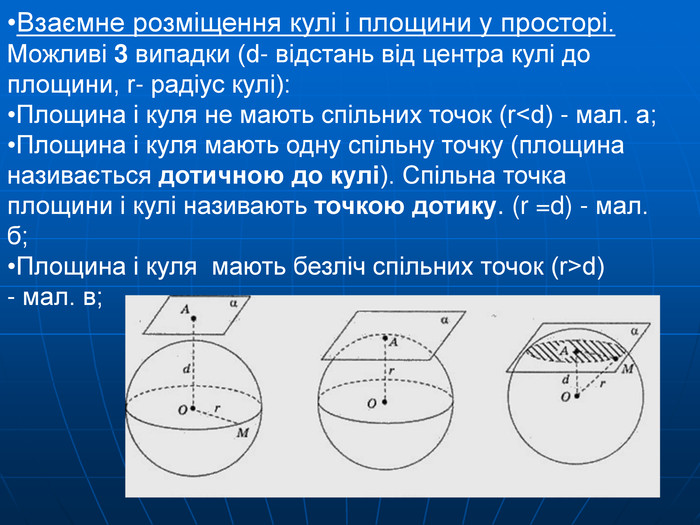
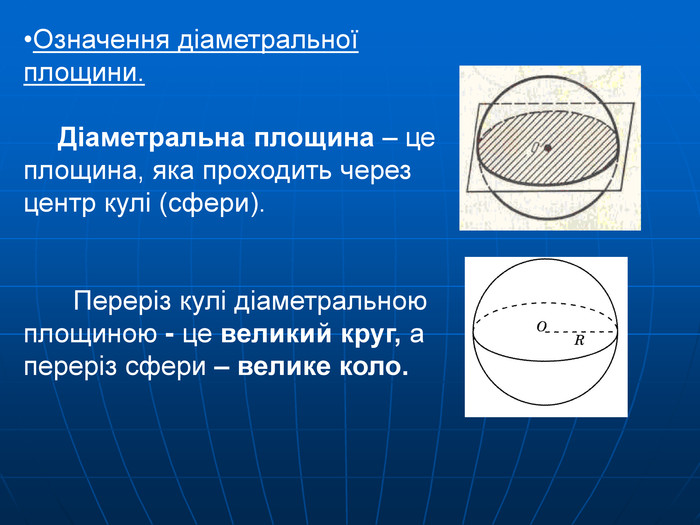
Переріз кулі площинами
Симетрія кулі
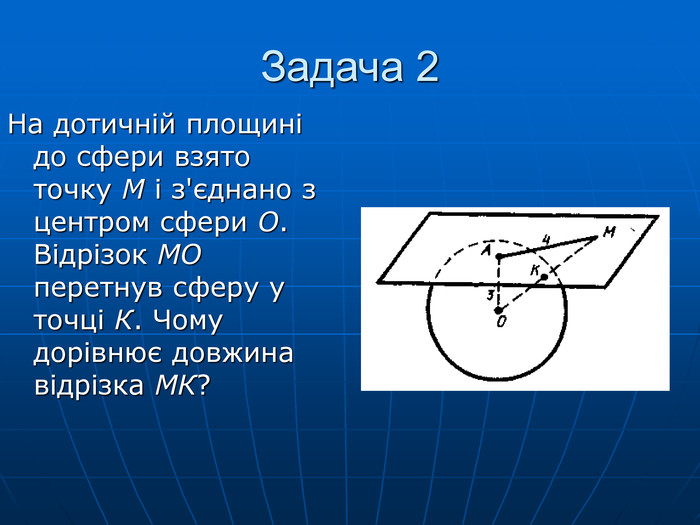
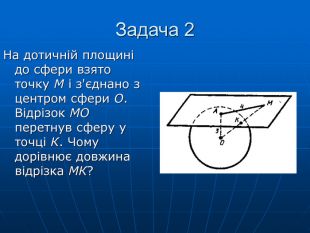
Дотична площина до кулі
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дякую! Успіхів!
-
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку