Презентація "Кути між прямими в просторі"

Кути між прямими в просторі10 кл. Алтинівський ліцей Кролевецької міської ради, Сумської областівчитель математики Грамм Елеонора Степанівна 2020-2021 н.р.

Дана тема актуальна, так як подібні задачі потребують абстрактного мислення. Задачі, які пропонуються нижче, частіше всього викликають в учнів затруднення при розв’язуванні. Наочне розв’язання дозволяє краще зрозуміти способи розв’язування таких задач

𝛼 Дві прямі, що перетинаються в просторі, визначають єдину площину, тому кут між прямими, що перетинаються в просторі визначається так як і в площині. Нагадаємо це означення: ав. МОзначення. Менший з нерозгорнутих кутів, утворених при перетині двох прямих, називається кутом між даними прямими. З означення слідує, що кут між двома прямими, які перетинаються не більший 900 Якщо прямі паралельні, то величина кута між ними дорівнює 00.(𝑎,𝑏)∈00, 900] 

Задача 1.(Усно)АВСDMNPР1 КДано: D (АВС),АМ = МD; ВN = ND; CP = PDК ВN. Визначити взаємне розміщення прямих:а) ND та ABб) РК та ВСв) МN та. AB

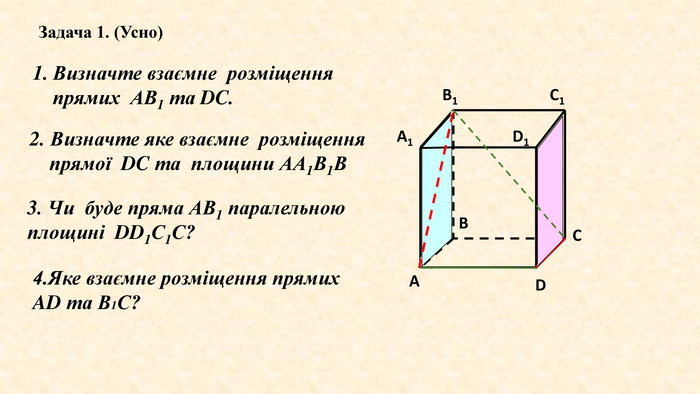
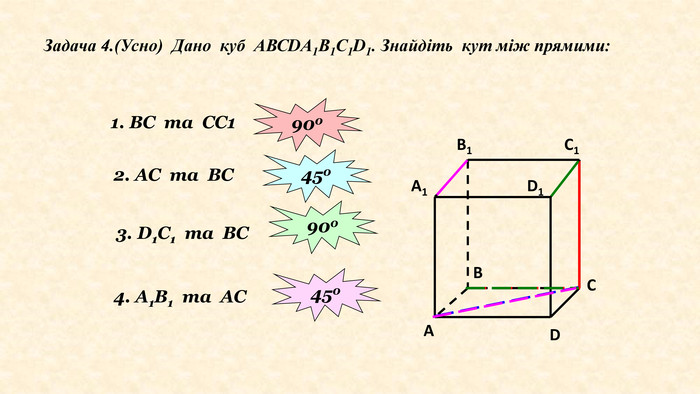
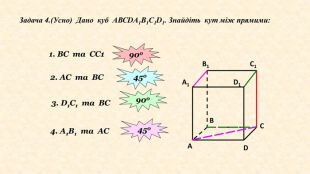
Задача 2. Дано куб ABCDA1 B1 C1 D1. Знайдіть кути між прямими: 1) CC1 та BC1; 2) BC1 та CB1; 3) AA1 та CC1; 4) A1 C1 та BC1.1)СС1⸦(ВВ1 С1), В С1⸦(ВВ1 С1), СС1⋂ ВС1=т. С1, ВВ1 С1 С - квадрат ( CC1; BC1) =BC1 C=450 (за властивістю діагоналей квадрата); 2) ВС1⸦(ВВ1 С1), В1 С ⸦(ВВ1 С1), ВС1 ⋂ В1 С= т. О, ВВ1 С1 С – квадрат, (BC1; CB1 ) =C1 ОC=900 (за властивістю діагоналей квадрата);BCC1 В1 О3) AA1⸦(АА1 С1), СС1⸦(АА1 С1), AA1║CC1 , тому (AA1; CC1 ) = 00 .4) A1 C1 ⸦(А1 В1 С1), ВС1⸦(ВВ1 С1), А1 В ⸦(АА1 В1), ∆А1 С1 В- рівносторонній, бо А1 С1=С1 В=А1 В, тому (A1 C1; C1 В)= A1 C1 B=600 (за властивістю рівностороннього трикутника ΔA1 C1 B);Відповідь: 1) 450; 2) 900; 3) 00; 4) 600. A1 B1 D1 ABDC1 СРозв’язання. О

A1 B1 D1 ABDC1 СЗадача 3. Дано прямокутний паралелепіпед ABCDA1 B1 C1 D1, AB=4см, ВС=3см, ВВ1=2 см. Знайдіть кути між прямими: 1) CC1 та BC1; 2) BC1 та CB1; 3) AA1 та CC1; 4) A1 C1 та BC1. Розв’язання1) СС1⸦(ВВ1 С1), ВС1⸦(ВВ1 С1), СС1⋂ ВС1=т. С1, ВВ1 С1 С –прямокутник, ВС1- його діагональ. З ∆ВСС1(ВСС1=900): ВССС1=tg BC1 C=1,5;  BC1 C=arctg1,556018’;  2) ВС1⸦(ВВ1 С1), В1 С ⸦(ВВ1 С1), ВС1 ⋂ В1 С= т. О, ВВ1 С1 С –прямокутник, В1 С та ВС1- його діагоналі і В1 С⋂ВС1= т. О, (BC1; CB1 ) =C1 ОC. ОЗ ΔOC1 C, OC=OC1: О =1800–2* С1= 1800–2arctg1,5 1800–112036’=67024’;(за теоремою про суму кутів трикутника та за властивістю рівнобедренного трикутника;3) AA1⸦(АА1 С1), СС1⸦(АА1 С1), AA1║CC1 , тому (AA1; CC1 ) = 00 .4) A1 C1 ⸦(А1 В1 С1), ВС1⸦(ВВ1 С1), А1 В ⸦(АА1 В1), ∆А1 С1 В. (A1 C1; C1 В)= A1 C1 B Сторони ΔA1 C1 B знаходим з прямокутних трикутників ΔA1 C1 D1, ΔAA1 B , ΔCC1 B за теоремою Піфагора: а) ΔА1 С1 D1(A1 D1 C1=900) :  𝐴1𝐶12=𝐴1𝐷12+𝐷1𝐶12  ; A1 C1=5 см; б) ΔAA1 B (А1 АВ=900) : A1 B= см, в) ΔCC1 B(С1 СВ=900): BC1= см.  Тепер, в Δ A1 C1 B за наслідком з теореми косинусів знаходимо A1 C1 B, маємо:

Кут між мимобіжними прямимиα1800 - α00 < α 9001.2. Кут між мимобіжними прямими. АВ та СD визначається, як кут між прямими, що перетинаються, прямими А1 В1 и С1 D1, при цьому А1 В1|| АВ и С1 D1|| CD. АВDСА1 В1 С1 D1αМ1

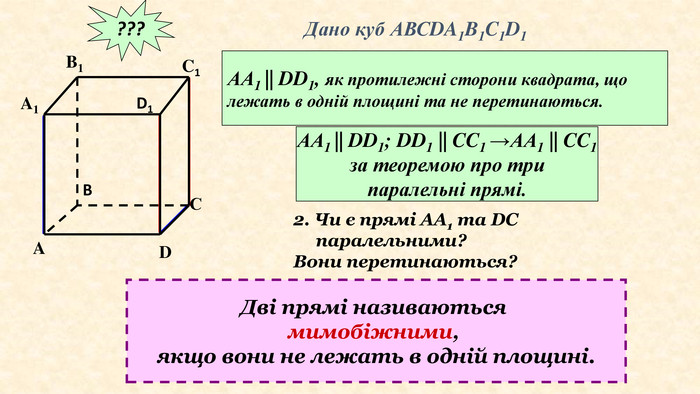
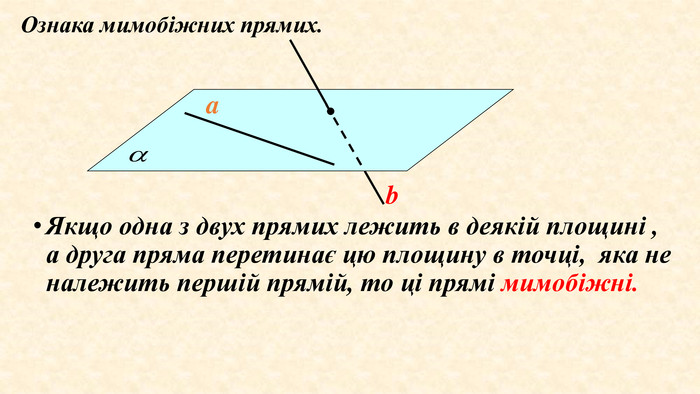
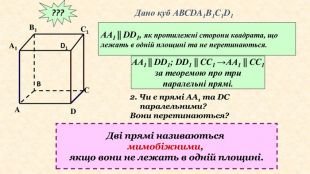
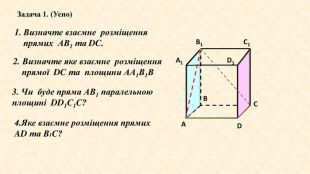
???Дано куб АВСDA1 B1 C1 D1 Чи будуть паралельними прямими прямі АА1 та DD1; АА1 та СС1 ?Чому?АА1 || DD1, як протилежні сторони квадрата, що лежать в одній площині та не перетинаються. АА1 || DD1; DD1 || CC1 →AA1 || CC1за теоремою про трипаралельні прямі.2. Чи є прямі АА1 та DC паралельними?Вони перетинаються?Дві прямі називаються мимобіжними, якщо вони не лежать в одній площині. A1 B1 D1 ABDC1 С

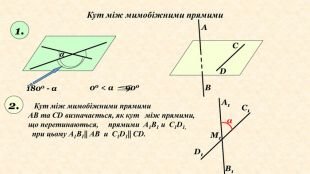
Практичне завдання. Вибрати довільну точку М2. Побудувати А2 В2|| АВ та С2 D2|| CD. Відповісти на запитання:1. Чому А2 В2|| А1 В1 та С2 D2|| C1 D1?2. Чи є кути А1 М1 D1 та А2 М2 D2 кутами з відповідно паралельними сторонами??Висновок:1. Величина кута між мимобіжнимипрямими не залежить від вибору точки.3.

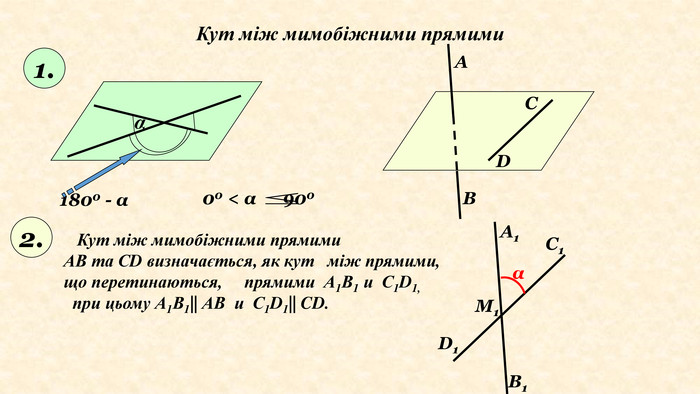
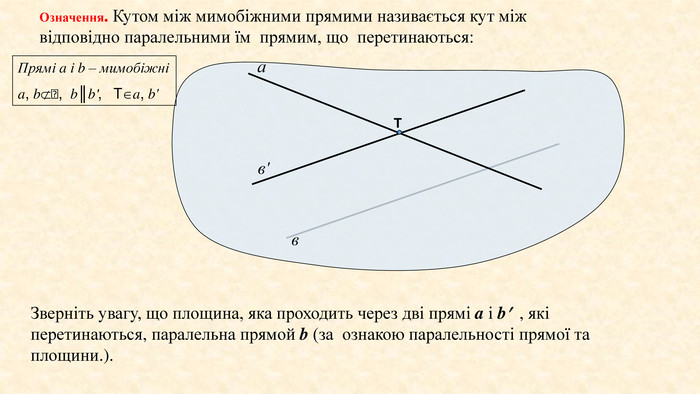
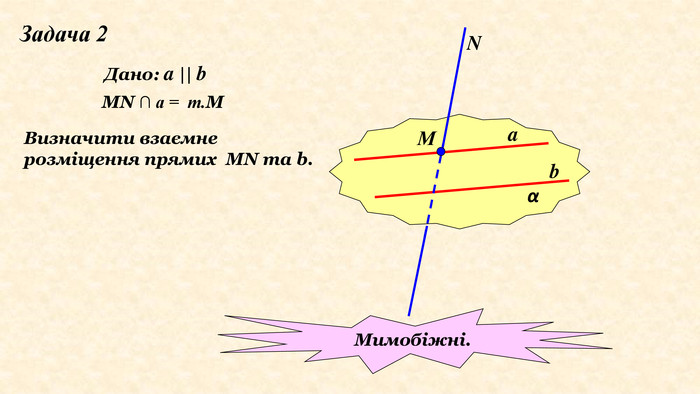
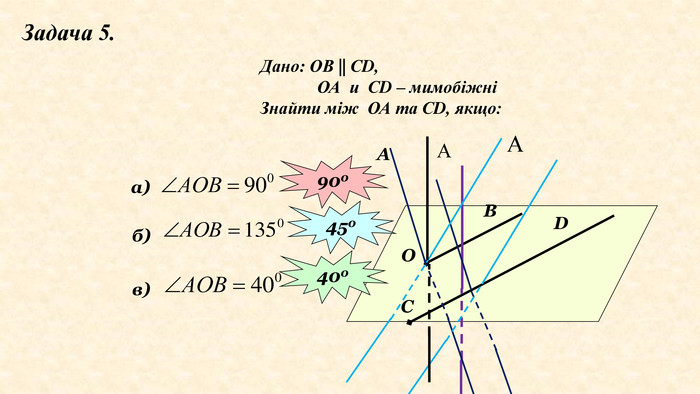
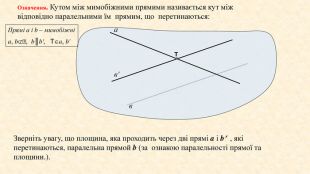
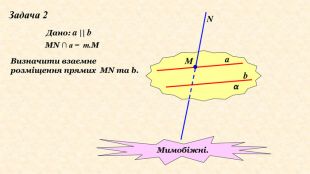
Означення. Кутом між мимобіжними прямими називається кут між відповідно паралельними їм прямим, що перетинаються:авв'TПрямі a і b – мимобіжніa, b, b║b', Ta, b'Зверніть увагу, що площина, яка проходить через дві прямі a і b , які перетинаються, паралельна прямой b (за ознакою паралельності прямої та площини.).

Ознака мимобіжних прямих. Якщо одна з двух прямих лежить в деякій площині , а друга пряма перетинає цю площину в точці, яка не належить першій прямій, то ці прямі мимобіжні.ab

C1 CA1 B1 D1 ABDВизначте взаємне розміщення прямих АВ1 та DC.2. Визначте яке взаємне розміщення прямої DC та площини АА1 В1 В3. Чи буде пряма АВ1 паралельною площині DD1 С1 С?Задача 1. (Усно)4. Яке взаємне розміщення прямих AD та В1 С?stroke.colorstroke.on

Задача 2αab. МNДано: a || b. MN ∩ a = т. MВизначити взаємне розміщення прямих MN та b. Мимобіжні.

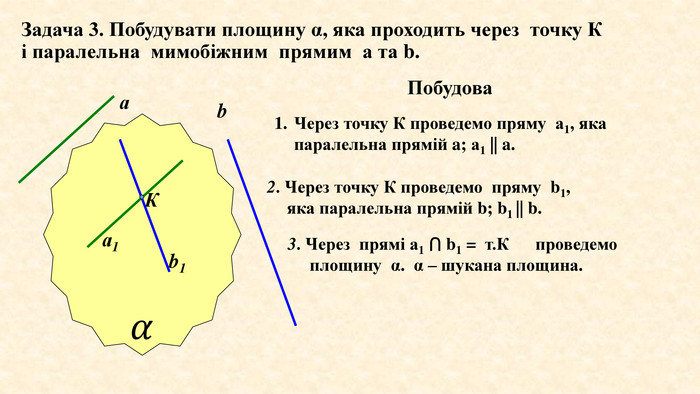
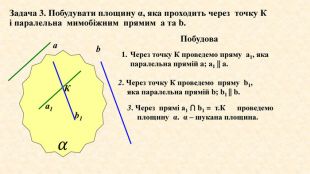
Задача 3. Побудувати площину α, яка проходить через точку К і паралельна мимобіжним прямим а та b. Через точку К проведемо пряму а1, яка паралельна прямій a; а1 || a.2. Через точку К проведемо пряму b1, яка паралельна прямій b; b1 || b.𝛼 аb. Ка1b13. Через прямі а1 ⋂ b1 = т. К проведемо площину α. α – шукана площина. Побудова

C1 CA1 B1 D1 ABDЗадача 4.(Усно) Дано куб АВСDА1 В1 С1 D1. Знайдіть кут між прямими:1. ВС та СС1 2. АС та ВС9004503. D1 С1 та ВС 9004. А1 В1 та АС 450

Задача 5. Дано: ОВ || СD, ОА и СD – мимобіжніЗнайти між ОА та СD, якщо: ОВCDа)900б)450в)400 AАА

Задача 6. Дано куб ABCDA1 B1 C1 D1. Знайдіть кут між прямими: 1) CC1 та АB; 2) AD1 та CB1; 3) AD1 та BA1; 4) DB1 та AA1; 5) BD1 та AC. Розв‘язання1)СС1 ⸦(DD1 С1), АВ ⸦(АВС), отже прямі СС1 та АВ – мимобіжні; АВ║DC, тому (СС1;АВ)= (CC1;DC)=900( за означенням квадрата). 2) AD1⸦(АА1 D1) та CB1⸦(BB1 C1), отже прямі AD1 та СВ1- мимобіжні; (АА1 D1) ║(BB1 C1),AD1║BC1, тому (AD1;CB1)= (ВС1;СВ1)= 900 – за властивістю діагоналей квадрата .  3) AD1 ⸦(АА1 D1) та BA1 ⸦(АА1 В1), отже прямі AD1 та BA1 -мимобіжні; (АА1 В1)║(DD1 С1), BA1║CD1, AC ⸦(АВС), AC – діагональ основи, AD1=D1 C=AC, ∆AD1 C- рівносторонній, тому(AD1;ВА1)= (AD1; D1 C)= AD1 C= 600. 4) DB1 ⸦(DD1 B1), AA1 ⸦(AA1 B1), отже прямі DB1 та AA1 - мимобіжні; АА1║ВВ1.  (DB1;AA1)=  (BB1;В1 D).5) DB1 ⸦(DD1 B1), AC ⸦(АВС), отже прямі DB1 та АС – мимобіжні; DB⋂AC = т. О, т. О∈DB, т. О∈АС. DB1║OK, т. К ∈ ВВ1, В1 К=КВ. (DB1;AC)=(KO;OA). ОК∆В1 ВD,  В1 ВD=900. Позначимо АА1=a= ВВ1 – ребра куба, тоді сторони ∆В1 ВD будуть: ВВ1=a, BD=𝑎2 , DB1=a3. cos ВВ1 D =𝐵𝐵1𝐷𝐵1=𝑎𝑎3=33  ВВ1 D= 𝑎𝑟𝑐𝑐𝑜𝑠33≈54042′. ∆АКС – рівнобедренний, основа АС, КО – медіана, бо АО=ОС, КО- висота, КО⊥АС, отже <КОА= 900, тому (DB1;AC)=(KO;OA)= 900. 

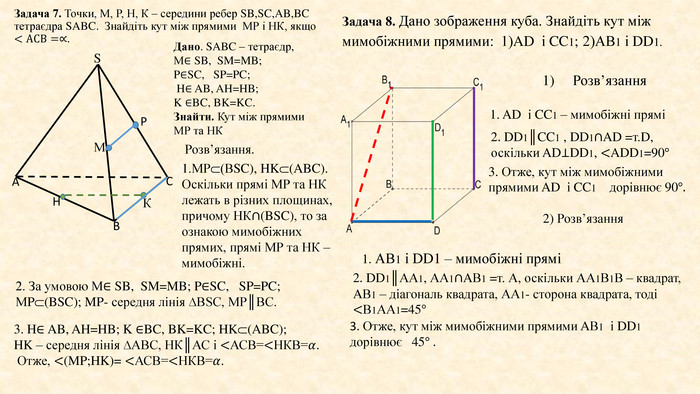
S Задача 7. Точки, М, Р, Н, К – середини ребер SB,SC,AB,BC тетраєдра SABC. Знайдіть кут між прямими МР і НК, якщо <АСВ=∝. АВСКНМРДано. SABC – тетраєдр,М∈ SB, SM=MB;P∈SC, SP=PC; H∈ AB, AH=HB; K ∈BC, BK=KC. Знайти. Кут між прямими МР та НК Розв’язання.1. МР⸦(ВSC), HK⸦(ABC). Оскільки прямі МР та НК лежать в різних площинах, причому НК∩(BSC), то за ознакою мимобіжних прямих, прямі МР та НК – мимобіжні. 2. За умовою М∈ SB, SM=MB; P∈SC, SP=PC; МP⸦(BSC); MP- середня лінія ∆ВSC, MP║BC. 3. H∈ AB, AH=HB; K ∈BC, BK=KC; HK⸦(ABC); HK – середня лінія ∆АВС, НК║АС і <АСВ=<НКВ=𝛼. Отже, <(MP;HK)= <АСВ=<НКВ=𝛼. Задача 8. Дано зображення куба. Знайдіть кут між мимобіжними прямими: 1)AD і CC1; 2)АВ1 і DD1.1) Розв’язання1. AD і CC1 – мимобіжні прямі2. DD1║CC1 , DD1∩AD =т. D, оскільки AD⊥DD1,

Задача 9. Знайдіть кут між мимобіжними прямими: 1)А1 В і В1 С; 2)A1 D1 і C1 D; 3)AB1 і D1 C. Розв‘язання1)1. А1 В і В1 С – мимобіжні. 2. Площини АА1 D1 D║ВВ1 C1 C, В1 С⸦ ВВ1 С1 С, то B1 C║A1 D.  3. Грані куба АА1 В1 В, АА1 D1 D, АВСD – рівні квадрати, А1 В, А1 D, BD –відповідно діагоналі цих квадратів, А1 В=А1 D=BD. Отже, ∆А1 ВD- рівносторонній, <ВА1 D= 60°. 4. Отже, кут між мимобіжними прямими А1 В і В1 С дорівнює 60°.  2)1. A1 D1 і C1 D – мимобіжні.2. A1 D1║ В1 С1, В1 С1⊥ (DD1 C1), C1 D ⸦(DD1 C1), тому В1 С1⊥С1 D,<В1 С1 D=90°.  3. Отже, кут між мимобіжними прямими A1 D1 і C1 D дорівнює 90°  3)1. АВ1 і D1 С - мимобіжні прямі. 2 Грані куба, АА1 В1 В║DD1 C1 C, АВ1⸦ (АА1 В1), D1 C⸦(DD1 C1). АВ1║DC1.3. DD1 C1 C – квадрат, D1 С, DC1 – діагоналі, D1 C⊥DC1, <(D1 C;DC1)= 90°. 4. Отже, кут між мимобіжними прямими AB1 і D1 C дорівнює 90° .  

Задача 10. Пряма SA перпендикулярна до сторін АВ і АС трикутника АВС. Знайти кут між прямими SA і ВС. Розв’язання1. SA⊥AB, SA⊥AC, ∆ABC (за умовою). Отже, за ознакою перпендикулярності прямої до площини SA⊥(ABC).2. ВС⸦(АВС), SA⊥(ABC), SA⋂(AВС)= т. А, т. А∉ВС, то за ознакою мимобіжних прямих, BC та SA – мимобіжні. BCASА1 SA1 Задача 11. Точки К і М середини ребер АВ і DC трикутної піраміди DABC, кожне ребро якої дорівнює a. Доведіть, що КМ⊥АВ. Знайдіть довжину відрізка КМ.3. За означенням перпендикулярності прямої до площини, маємо, що SA⊥BC, і кут між мимобіжними прямими SA і ВС дорівнює 90°.  КМDCABРозв’язання1. DABC - трикутна піраміда, кожне ребро якої дорівнює a. 2. Точка Кϵ АВ, АК=КВ, т. М∈DC; DM=MC АВ і DC – мимобіжні. Доведемо, що КМ⊥АВ. 3. Розг. ∆ADC, за умовою задачі AD=DC=AC=a та DM=MC. Отже, АМ – медіана цього трикутника, МС=12a та АМ – висота, тобто АМ⊥DС. ∆АМС(<АМС=90°), за наслідком з теореми Піфагора, маємо: АМ2=АС2−МС2. АМ= 𝑎2−(𝑎2)2=3𝑎24= 𝑎23. Аналогічно встановлюємо довжину ВМ. Маємо, що ВМ= АМ, ∆АМВ – рівнобедренний та за умовою задачі АК=КВ=12a, МК – медіана, а отже МК⊥АВ. Доведено. З ∆МКВ, знаходимо КМ. КМ= 3𝑎24−(𝑎2)2=2𝑎24 =𝑎22. 

Задача 12. Знайдіть кут між мимобіжними діагоналлю куба і діагоналлю грані куба. Розв’язання1. Знайдемо кут між діагоналлю B1 D куба і діагоналлю А1 В грані куба. 2. Добудуємо до даного куба ABCDA1 B1 C1 D1 куб ВКТСВ1 РМС1.3. Оскільки В1 D та А1 В – мимобіжні, то кут між ними дорівнює куту між прямими В1 D і В1 К , бо А1 В║В1 К.4. Введемо допоміжну змінну. Нехай АВ=a, тоді А1 В=a2, A1 B=B1 K, отже В1 К =a2. В1 D= 𝑎2+𝑎2 +𝑎2 = a3. 5. Рзгл. ∆КСD: DC=a, KC=a2, < KCD =135°, тоді за теоремою косинусів маємо, що𝐷𝐾2=𝐷𝐶2+𝐾𝐶2−2∗𝐷𝐶∗𝐾𝐶∗𝑐𝑜𝑠<𝐾𝐶𝐷; DK=𝑎2+2𝑎2−2∗𝑎∗𝑎2∗𝑐𝑜𝑠135°=3∗𝑎2+2∗𝑎2 =a5. 6. Із ∆КВ1 D маємо: 𝐷𝐾2=𝐷𝐵12+𝐵1𝐾2−2∗𝐷𝐵1∗𝐵1𝐾∗𝑐𝑜𝑠<𝐷𝐵1𝐾, (теорема косинусів).5*𝑎2=2*𝑎2+3*𝑎2-2*3*a*2*a*cos <𝐷𝐵1𝐾; 2*6*𝑎2* cos <𝐷𝐵1𝐾=0; звідси cos <𝐷𝐵1𝐾=0, <𝐷𝐵1𝐾=90°. Отже, DB1⊥B1 K, (B1 K║A1 B), тому кут між мимобіжними А1 В та В1 D дорівнює 90°. ABCDA1 B1 C1 D1 KTPM