Презентація "Квадрат, його властивості та ознаки"
Про матеріал
Презентація на тему: "Квадрат, його властивості та ознаки" призначена для візуального супроводу матеріалу, який розглядається під час вивчення теми. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


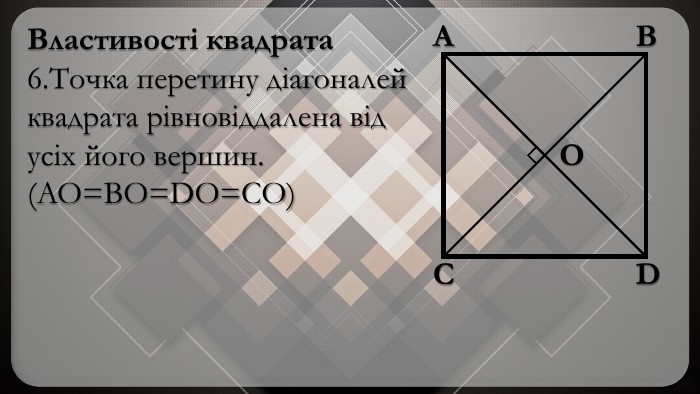






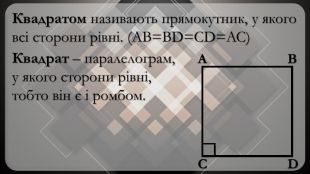
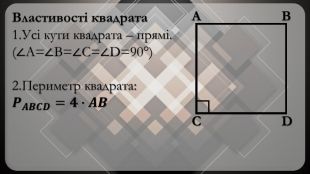
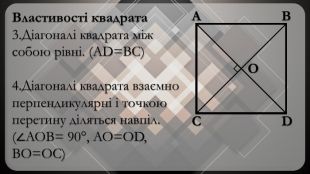






-

Юхименко В'ячеслав
01.11.2024 в 12:57
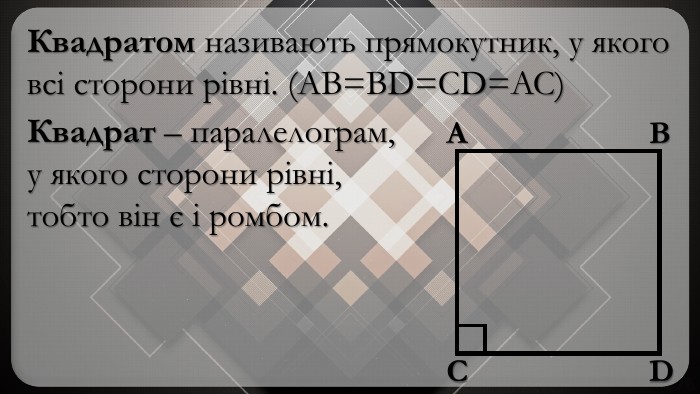
Колежанко, кожен квадрат є ромбом ;)
Загальна:
4.0
Структурованість
4.0
Оригінальність викладу
4.0
Відповідність темі
4.0
-

Моргун Любов Вікторівна
12.10.2023 в 16:55
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

САБУРОВА ВАЛЕНТИНА
02.10.2023 в 14:54
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Плішак Інна
15.07.2023 в 13:33
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук