Презентація "Паралелограм"
Про матеріал
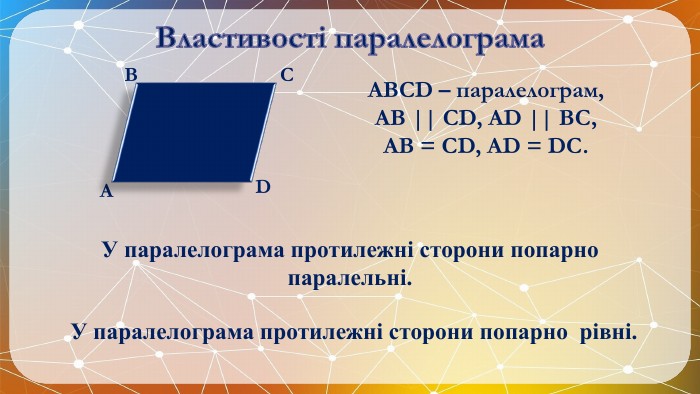
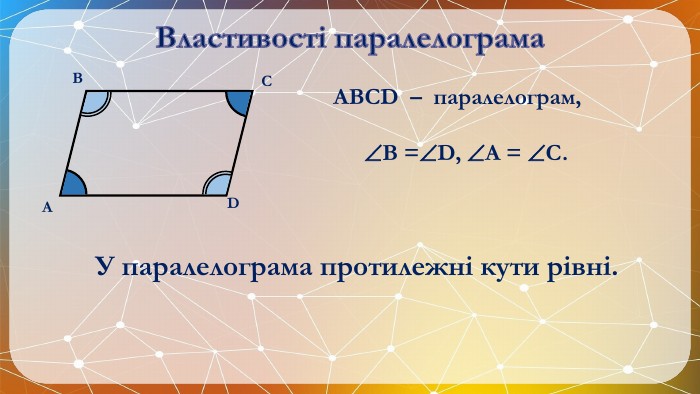
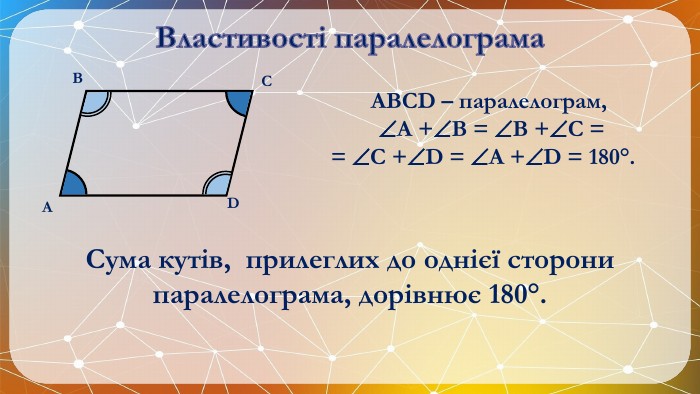
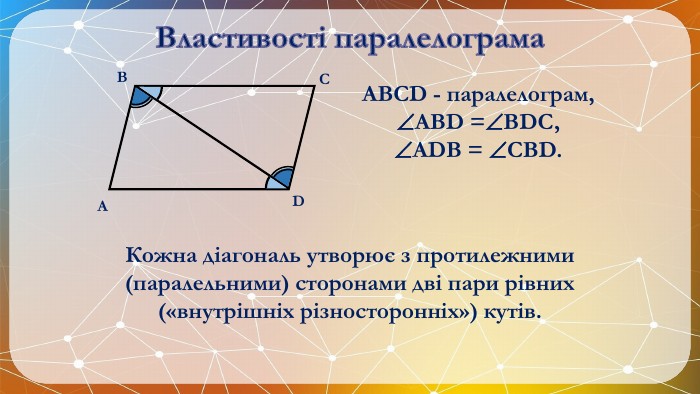
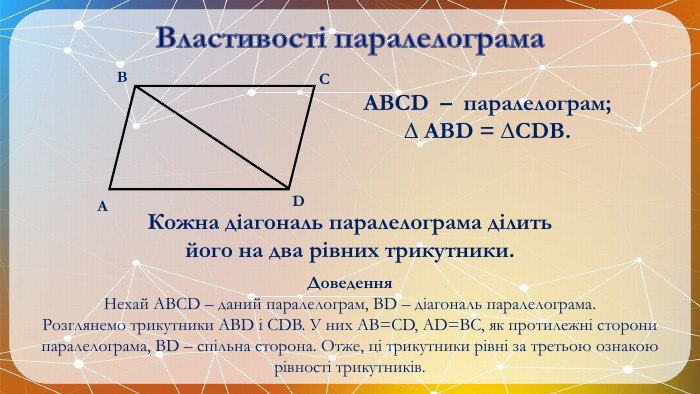
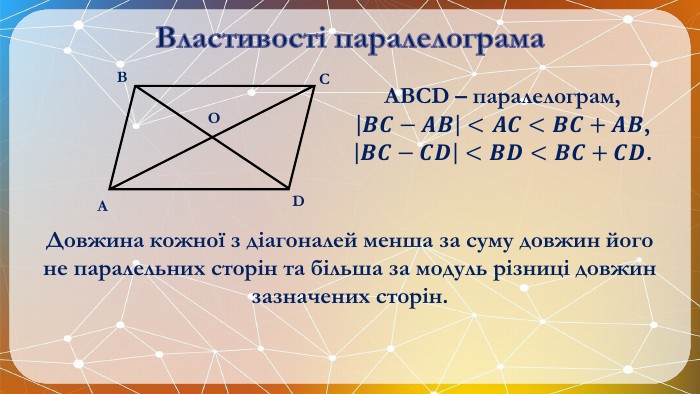
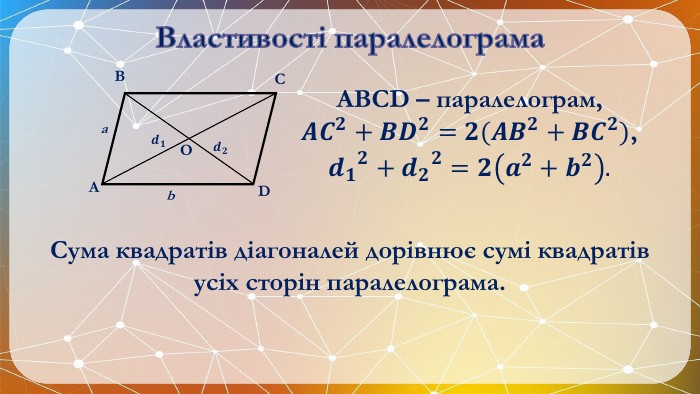
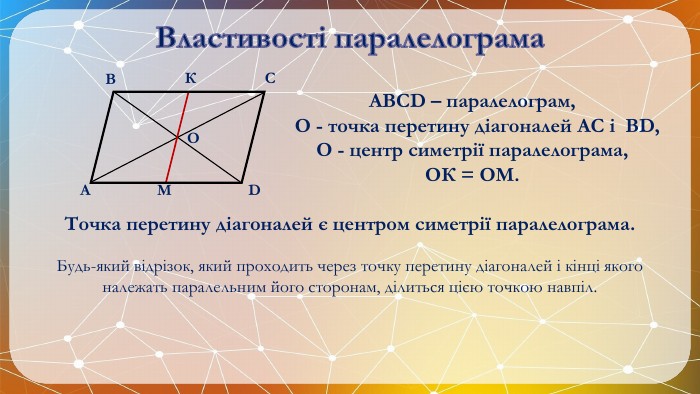
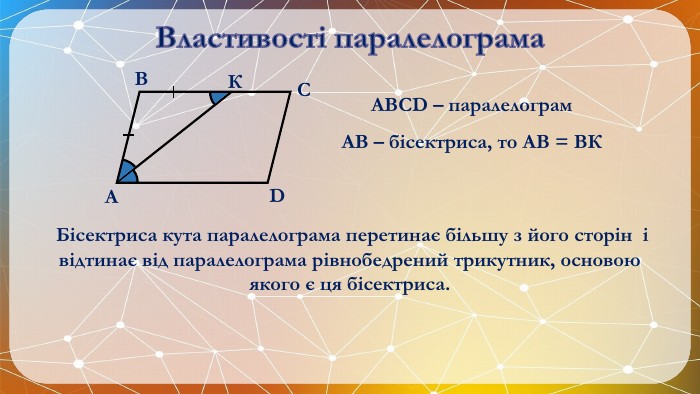
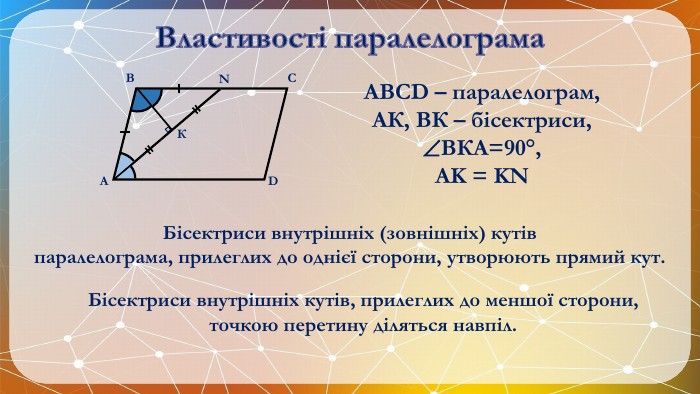
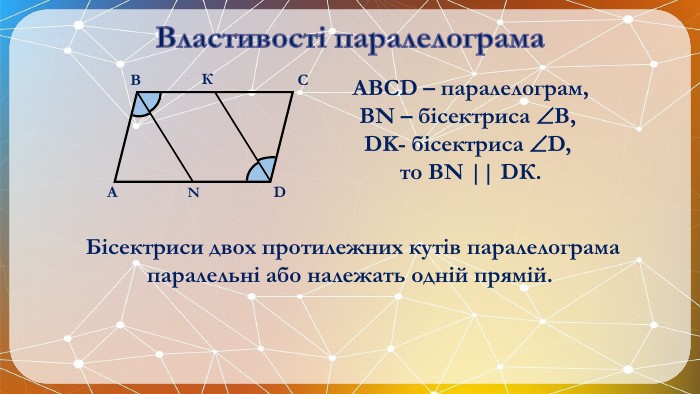
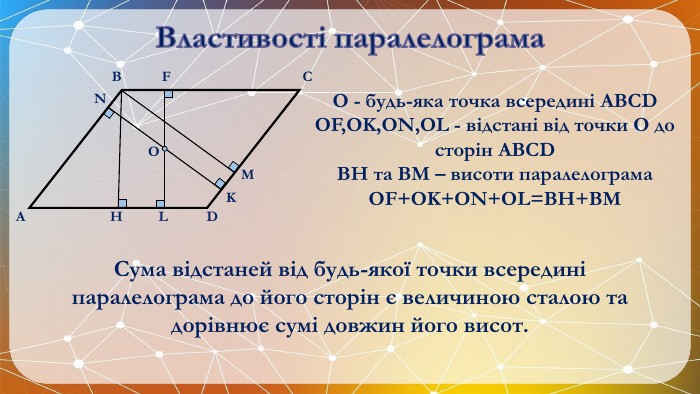
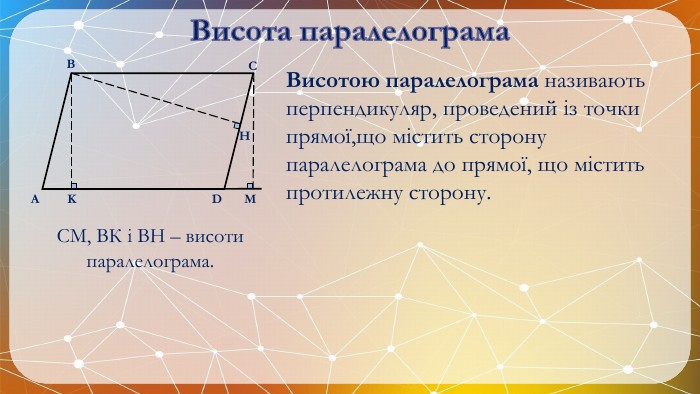
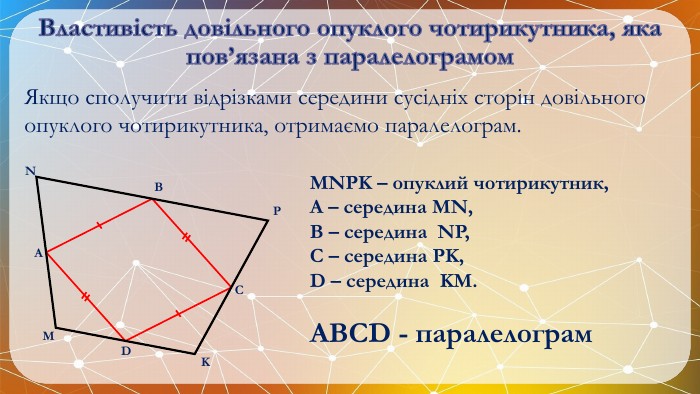
Презентація на тему: "Паралелограм" призначена для візуального супроводу матеріалу, який розглядається під час вивчення теми. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дуже змістовна презентація
-
-
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку