Презентація "Ромб, його властивості"
Про матеріал
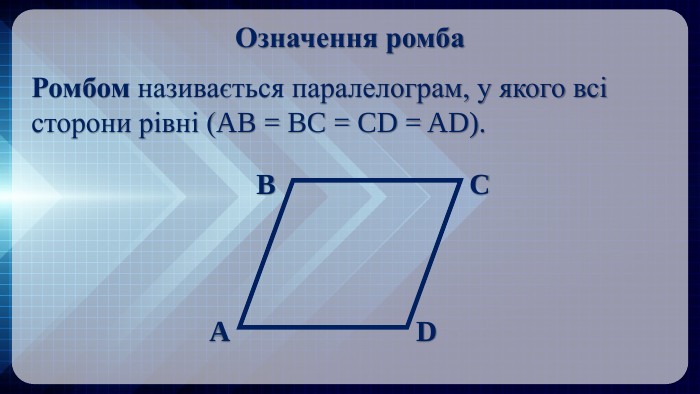
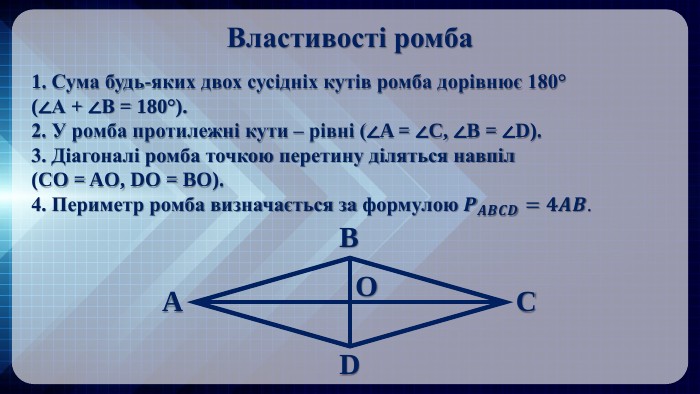
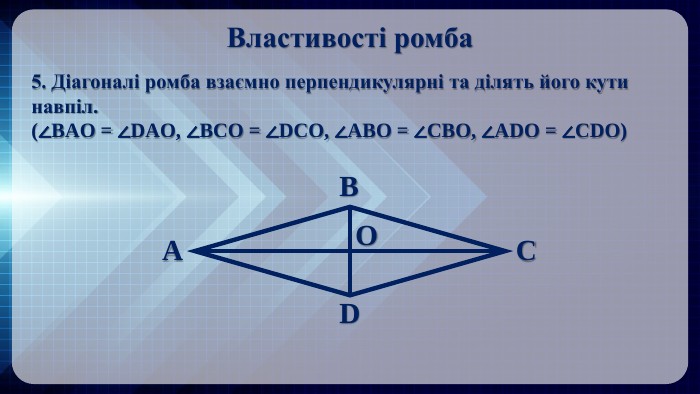
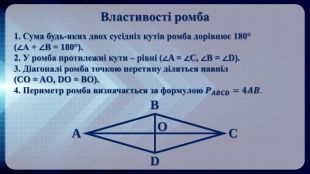
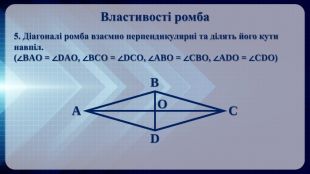
Презентація на тему: "Ромб" призначена для візуального супроводу матеріалу, який розглядається під час вивчення теми. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку















-

Тодоренко Оксана Василівна
26.09.2024 в 15:48
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мирошниченко Зоя Михайлівна
20.09.2024 в 09:07
Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

САБУРОВА ВАЛЕНТИНА
02.10.2023 в 14:53
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Брижатенко Марина Олексіївна
28.09.2023 в 08:32
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Колесник Наталія Іванівна
25.09.2023 в 22:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука