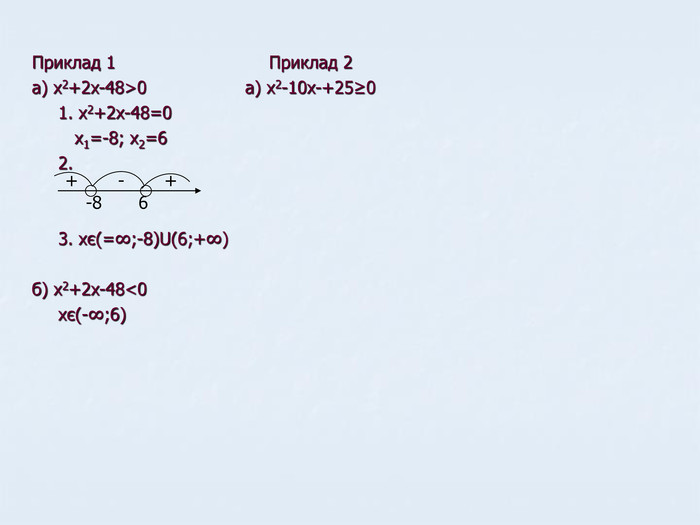
Презентація Квадратична функція
Про матеріал
Презентація Квадратична функція дає можливість вчителю
системазувати матеріал з даної теми,а учням повторити матеріал. Перегляд файлу
Зміст слайдів
ppt
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



![(-∞; (-b-√D)/2a)U ((-b+√D)/2a;+∞) ((-b-√D)/2a; (-b+√D)/2a) y<0 y=-b/2a
____ _____
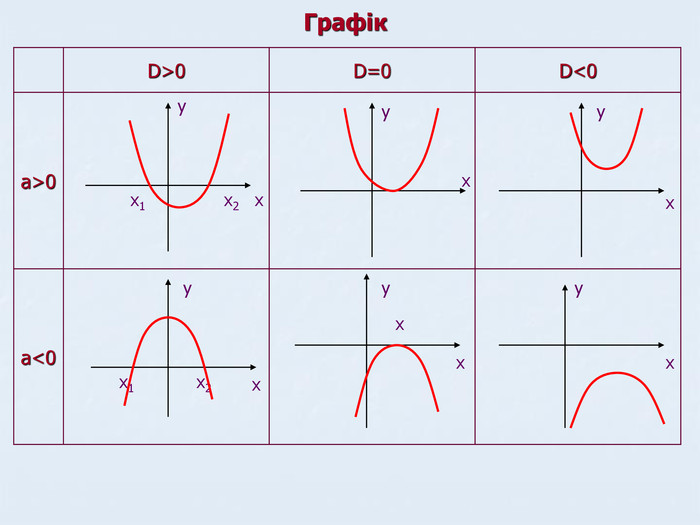
y=-b/2a 6. Найбільше та найменше значення ((-b-√D)/2a; (-b+√D)/2a) (-∞; (-b-√D)/2a)U ((-b+√D)/2a;+∞) 5. Проміжки снакосталості: y>0 [-b/2a;+∞) спадає (-∞;-b/2a] [-b/2a;+∞) 4. Монотонність: зростає при x=(-b±√D)/2a при x=(-b±√D)/2a 3. Нулі функції: y=0 (-∞;-b/2a) [-b/2a;+∞) 2. E(f) R R 1. D(f) a<0 a>0 властивості II Властивості функції (-∞; (-b-√D)/2a)U ((-b+√D)/2a;+∞) ((-b-√D)/2a; (-b+√D)/2a) y<0 y=-b/2a
____ _____
y=-b/2a 6. Найбільше та найменше значення ((-b-√D)/2a; (-b+√D)/2a) (-∞; (-b-√D)/2a)U ((-b+√D)/2a;+∞) 5. Проміжки снакосталості: y>0 [-b/2a;+∞) спадає (-∞;-b/2a] [-b/2a;+∞) 4. Монотонність: зростає при x=(-b±√D)/2a при x=(-b±√D)/2a 3. Нулі функції: y=0 (-∞;-b/2a) [-b/2a;+∞) 2. E(f) R R 1. D(f) a<0 a>0 властивості II Властивості функції](/uploads/files/461847/112278/119826_images/3.jpg)
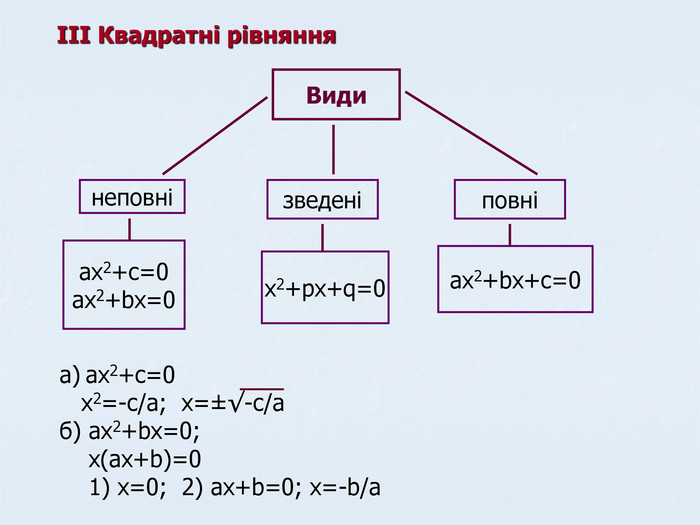
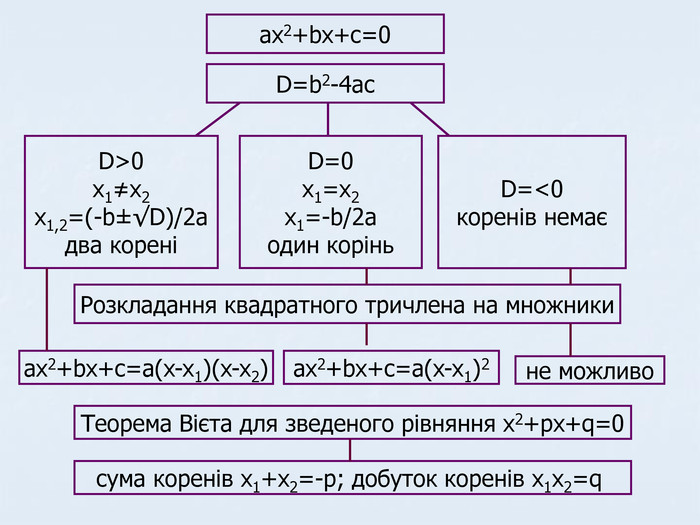

![Розв’язків немає x=x1 [x1;x2] ax2+bx+c≤0 xєR xєR xє(-∞;x1]U[x2;+∞) ax2+bx+c≥0 Розв’язків немає Розв’язків немає xє(x1;x2) ax2+bx+c<0 xєR xє(∞;x1)U(x1;+∞) xє(-∞;x1)U(x2;+∞) ax2+bx+c>0
D<0 D=0 D>0 Розв’язків немає x=x1 [x1;x2] ax2+bx+c≤0 xєR xєR xє(-∞;x1]U[x2;+∞) ax2+bx+c≥0 Розв’язків немає Розв’язків немає xє(x1;x2) ax2+bx+c<0 xєR xє(∞;x1)U(x1;+∞) xє(-∞;x1)U(x2;+∞) ax2+bx+c>0
D<0 D=0 D>0](/uploads/files/461847/112278/119826_images/8.jpg)