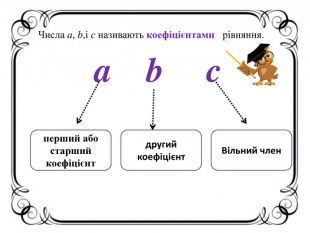
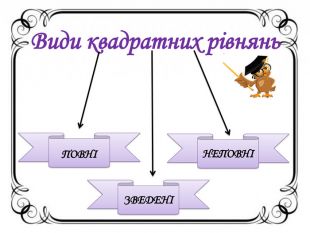
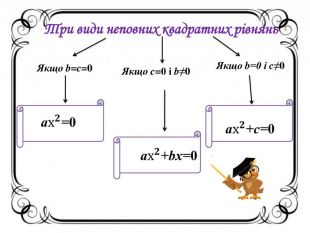
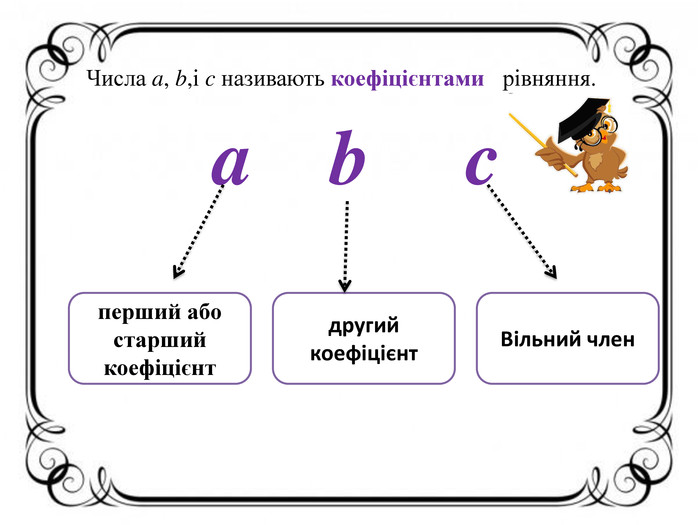
Презентація " Квадратні рівняння. Неповні квадратні рівняння".
Про матеріал
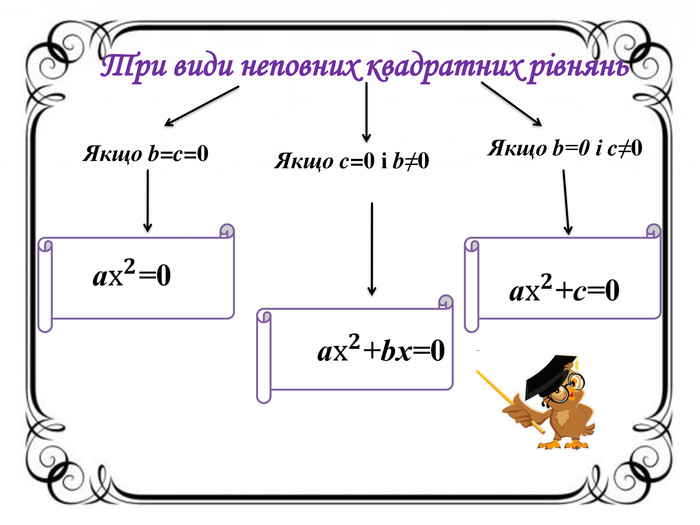
Ознайомити учнів з означенням квадратного рівняння та його видами, видами неповних квадратних рівнянь; сформувати вміння розрізняти неповні квадратні рівняння; розвивати логічне мислення учнів; виховувати уважність учнів.
Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра 8 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
§ 3. Квадратні рівняння Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку






![Історичні відомості про квадратні рівнянняІндія. Завдання, які розв'язувалися за допомогою квадратних рівнянь, зустрічаються в трактаті з астрономії «Аріабхаттіам», написаним індійським астрономом і математиком Аріабхатою І в 499 році нашої ери. Один з перших відомих висновків формули коренів квадратного рівняння належить індійському вченому Брамагупті (близько 598 г.) [1]; Брамагупта виклав універсальне правило розв'язування квадратного рівняння, зведеного до канонічного вигляду: ах2+bx+c=0,причому передбачалося, що в ньому всі коефіцієнти, крім а , можуть бути від'ємними. Сформульоване вченим правило по своїй суті збігається з сучасним. Історичні відомості про квадратні рівнянняІндія. Завдання, які розв'язувалися за допомогою квадратних рівнянь, зустрічаються в трактаті з астрономії «Аріабхаттіам», написаним індійським астрономом і математиком Аріабхатою І в 499 році нашої ери. Один з перших відомих висновків формули коренів квадратного рівняння належить індійському вченому Брамагупті (близько 598 г.) [1]; Брамагупта виклав універсальне правило розв'язування квадратного рівняння, зведеного до канонічного вигляду: ах2+bx+c=0,причому передбачалося, що в ньому всі коефіцієнти, крім а , можуть бути від'ємними. Сформульоване вченим правило по своїй суті збігається з сучасним.](/uploads/files/2246456/238711/258110_images/9.jpg)