Презентація "Математика і спорт"
Про матеріал
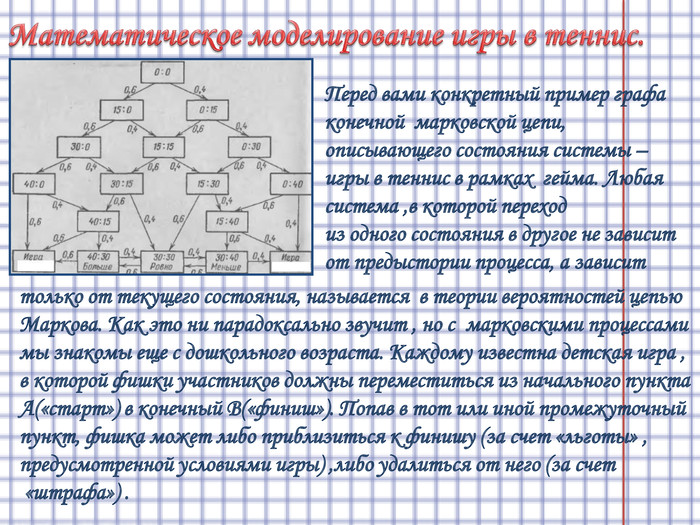
Матеріал может бути використаним на уроках математи для активізації інтересу до предмета. Спорт є прикладом використання цариці наук у повсякденному житті. Матеріал і є тим містком між безликими цифрами та їх практичним і цікавим використанням учнями на уроках та поза ними.
Зміст архіву
Перегляд файлу
Зміст слайдів
zip
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку