Презентація «Многогранник та його елементи»

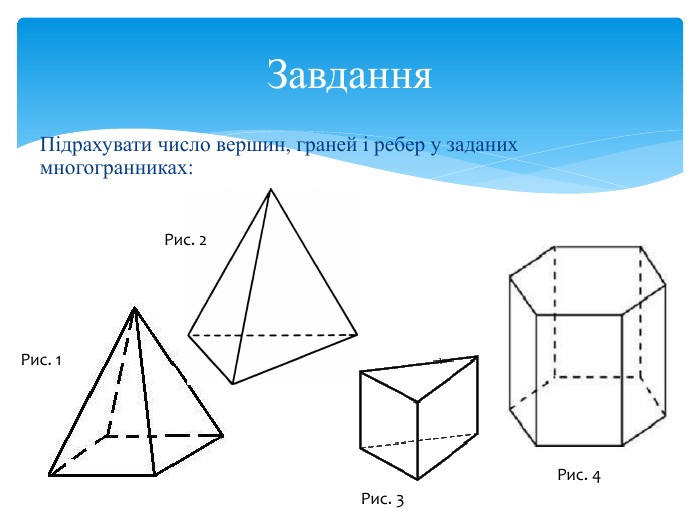
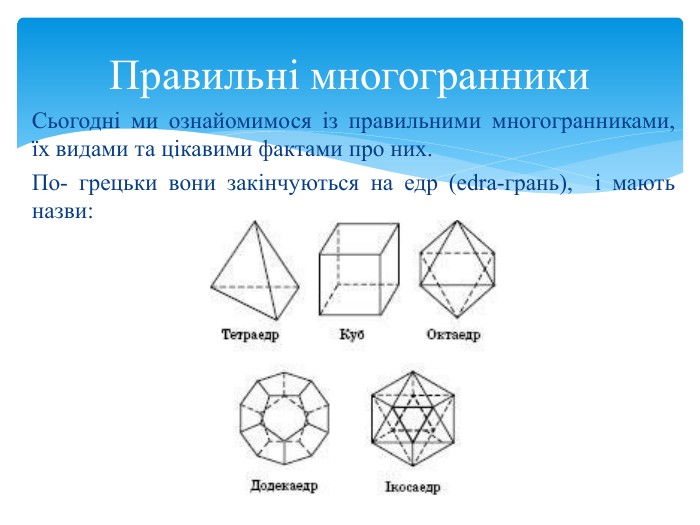
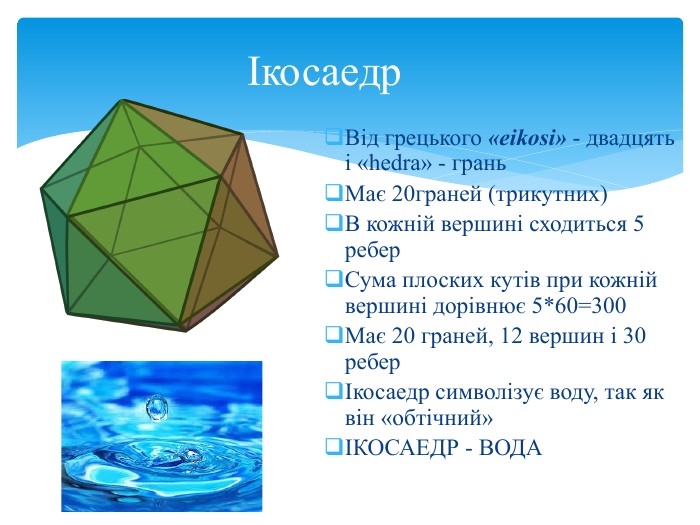
Відкрите лекційне заняття з дисципліни «Математика» для студентів ІІ курсу спеціальності 223 «Медсестринство»Тема: «Многогранник та його елементи»Комунальний заклад Львівської обласної ради«Самбірський фаховий медичний коледж»Циклова комісія загальноосвітніх дисциплін. Викладач: Мар'яна Кулькевич. Фрмат: On-line. Застосунок: Meet

Заняття №1з дисципліни «Математика»для студентів ІІ курсуспеціальності223 Медсестринство. Викладач: Мар'яна КУЛЬКЕВИЧСамбір 2023 Комунальний заклад Львівської обласної ради«Самбірський фаховий медичний коледж»Циклова комісія загальноосвітніх дисциплін

Многогранники навколо нас. Людина проявляє інтерес до многогранників та многокутників протягом усього свого життя – від дворічної дитини, що бавиться дерев'яними кубиками, до зрілого математика. Це пов'язано з красою і досконалістю форм, які досить часто зустрічаються у природі і сьогодні ми в цьому переконаємось.

Не випадково кажуть, що піраміда Хеопса – німий трактат геометрії. Грецька архітектура – зовнішнє вираження геометрії Евкліда. Многогранники. Форми многогранників застосовуються в конструюванні складних многогранних поверхонь. Йде це з глибокої давнини

Многогранники Поняття многогранника є одним із центральних у курсі стереометрія. Многогранники дають особливо багатий матеріал для розвитку поєднання живої просторової уяви із строгою логікою, яка складає суть геометрії.

Тематичні запитання: Де, навіщо і для чого нам потрібні багатогранники?Чи можливо в житті обійтися без них?Змістовні запитання: Що називається многогранником?Які елементи містить многогранник?Які многогранники називаються правильними?Скільки їх існує і чому?Що таке Ейлерева характеристика?На ці і багато інших запитань ми сьогодні і дамо відповідь. Ключове запитання. Чи залежить краса світу від математики???

Хочеться почати зі слів Бертрана Рассела:«Математика володіє не тільки істиною, але і вищою красою, красою відточеною і строгою, піднесено чистою і прагне до справжньої досконалості, яка властива, лише, найбільшим зразкам мистецтва»Запрошую у світ багатогранників)

Тема заняття: «Многогранник та його елементи. Правильні многогранники»

Навчальна. Ознайомлення студентів з поняттям многогранника та його елементів, правильного многогранника, видів правильних многогранників. Розвиваюча Розвиток логічного мислення, просторової уяви, математичної культури та спостережливості. Виховна Формування компетентності у сфері самостійної пізнавальної діяльності, виховання мовної культури та інтересу до вивчення математики, розвиток творчих здібностей та навичок роботи у команді. Мета заняття

Предметна – сформувати поняття многогранника, правильного многогранника. Вивчити правильні многогранники та теорему Ейлера. Ключові компетентності: Мовна - грамотно висловлюватися, лаконічно та стисло формулювати думку;Полікультурна – використання інформації з художньої літератури та історії математичних відкриттів;Математичні – вміння оперувати геометричними об'єктами в просторі; Інформаційна – стимулювання студентів до знаходження та використання додаткової інформаціїФормування компетентностей:

Поняття многогранника. Елементи многогранника. Теорема Ейлера. Розв'язування вправ. Правильні многогранники та їх види. Презентація студентських проєктів «Многогранники навколо нас»План

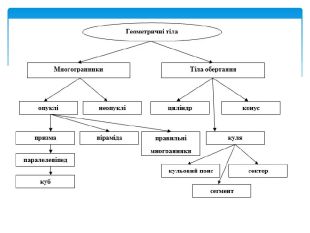
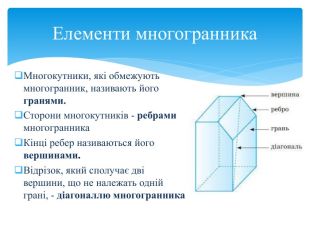
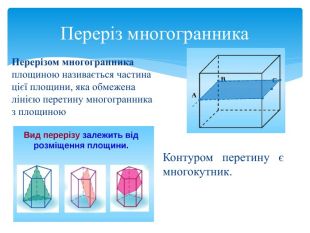
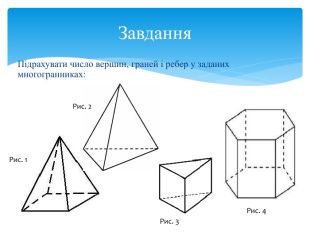
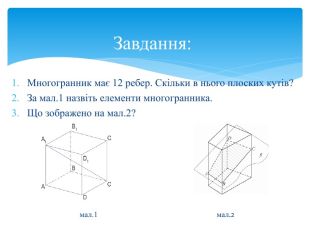
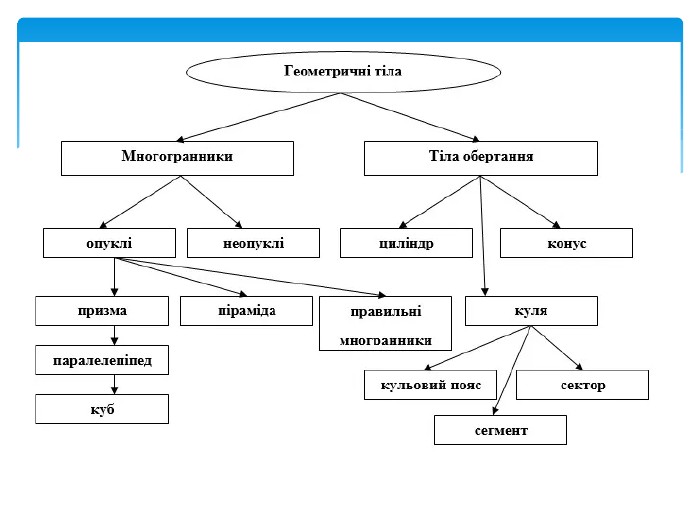
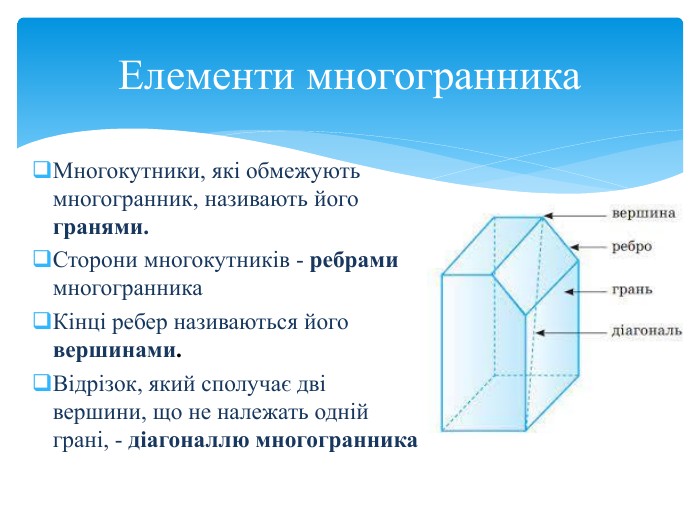
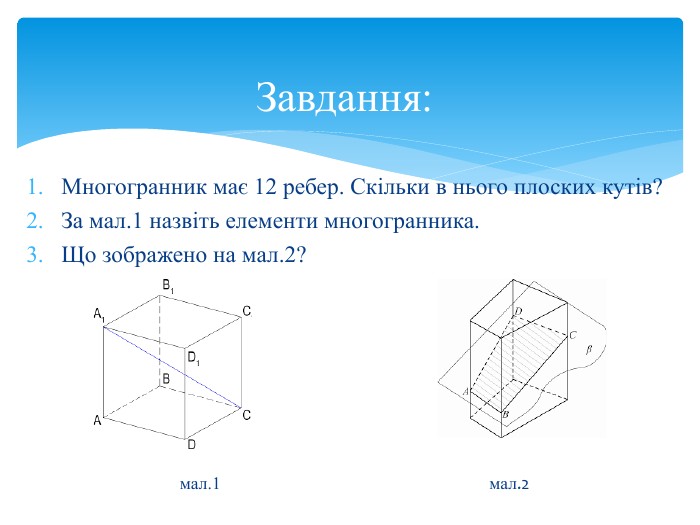
Многогранник (багатогранник) – геометрична фігура, частина тривимірного Евклідового простору, обмежена замкненою поверхнею, яка складається з плоских многокутників – граней многогранника. Многогранник – внутрішня частина простору, що обмежена багатокутниками, які називають гранями. Многогранник – це геометричне тіло, поверхня якого складається із скінченного числа плоских многокутників. Геометричні тіла, сторони яких у тривимірному просторі утворені обмеженими площинами, носять назву многогранники. Основні означення

Види многогранників налічують не один десяток представників. Тим не менш, у всіх є загальні властивості – три невід'ємних компоненти: грань;вершина;ребро. Властивості многогранників

Многокутники, які обмежують многогранник, називають його гранями. Сторони многокутників - ребрами многогранника. Кінці ребер називаються його вершинами. Відрізок, який сполучає дві вершини, що не належать одній грані, - діагоналлю многогранника. Елементи многогранника

Многогранники. Опуклі - тіло лежить по одну сторону площини будь якої його граніНеопуклі

Знайти опуклі і неопуклі многогранники. Рис. 2

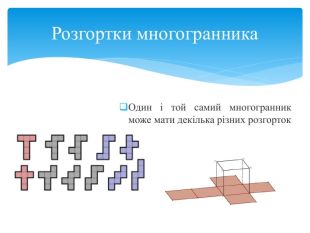
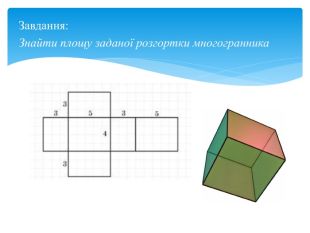
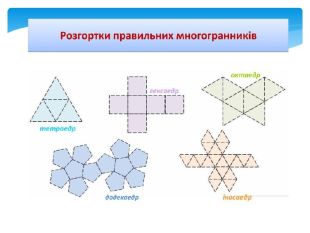
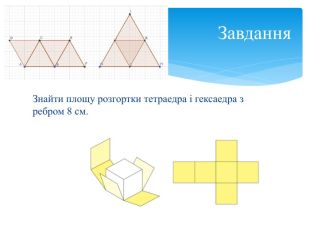
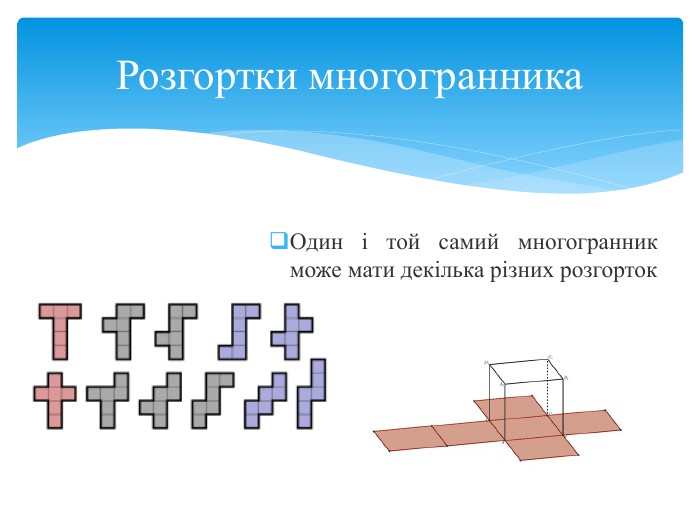
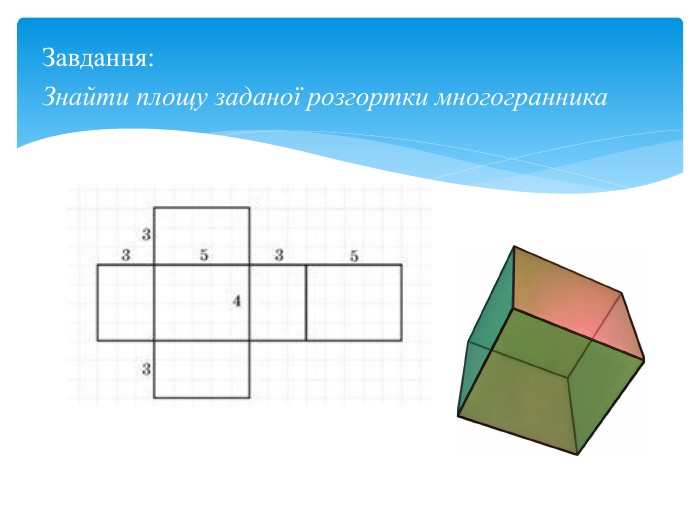
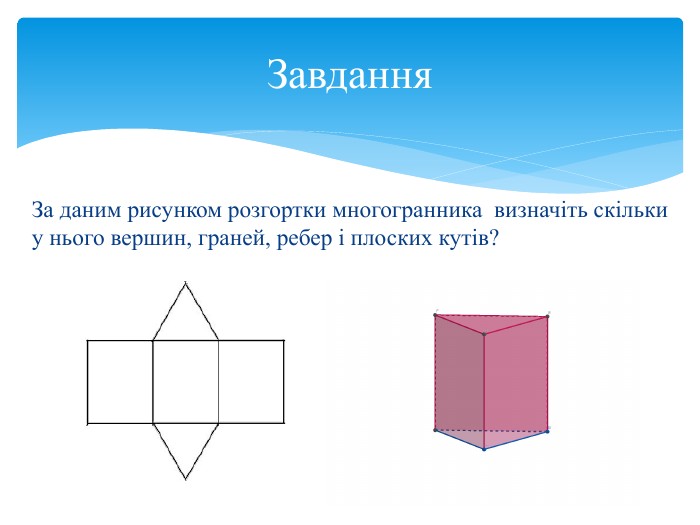
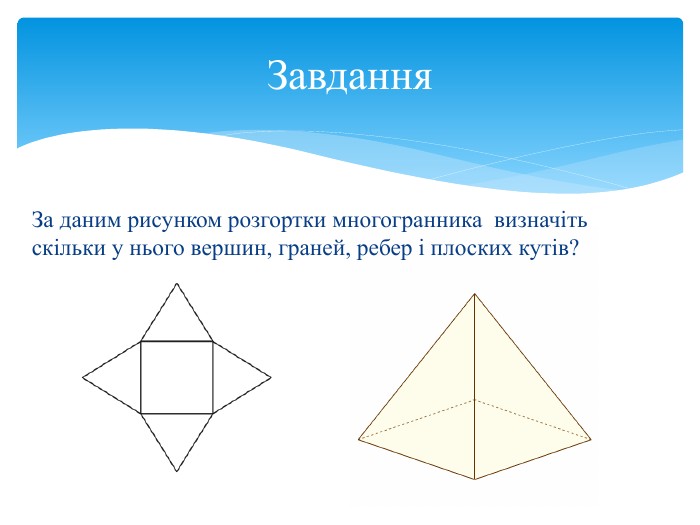
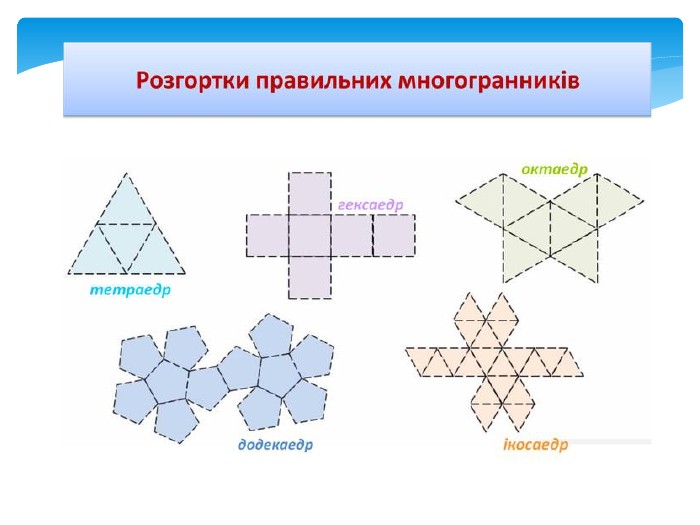
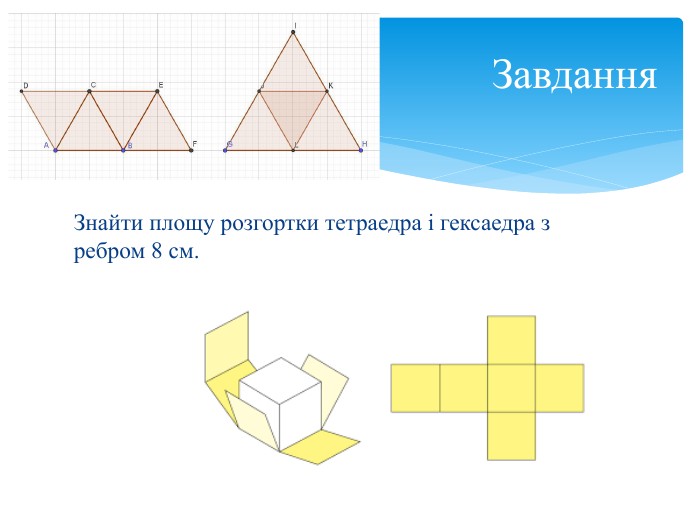
Многогранна поверхня – поверхня, утворена з скінченного числа плоских многокутників. Зображаючи многогранник на площині ми зображаємо сітку многогранника, яка складається з вершин і ребер. Розгортка многогранника являє собою плоский многокутник, складений з менших многокутників – граней вихідного многогранника. Площа поверхні многогранника дорівнює площі його розгортки. Розгортка многогранника

Один і той самий многогранник може мати декілька різних розгорток Розгортки многогранника

Завдання: Знайти площу заданої розгортки многогранника

Перерізом многогранника площиною називається частина цієї площини, яка обмежена лінією перетину многогранника з площиною. Переріз многогранника. Контуром перетину є многокутник.

Діагональний переріз. Діагональною площиною многогранника називається площина, що проходить через три вершини многогранника які не належать одній грані. Число плоских кутів многогранника в два рази більше числа його ребер.

Для кожного опуклого многогранника сума числа вершин - В і числа граней – Г на два більша за число його ребер –Р. Відомий швейцарський математик Ейлер відкрив і довів знамениту формулу В – Р + Г = 2 Теорема Ейлера

Вперше це співвідношення виявив Рене Декарт у 1752р. Ту саму формулу відкрив Леонард Ейлер, коли описував типи опуклих многогранників, залежно від числа їхніх вершин. Нині її називають формулою Ейлера.Історична довідка

Підрахувати число вершин, граней і ребер у заданих многогранниках: Завдання Рис. 1 Рис. 2 Рис. 3 Рис. 4

За даним рисунком розгортки многогранника визначіть скільки у нього вершин, граней, ребер і плоских кутів?Завдання

За даним рисунком розгортки многогранника визначіть скільки у нього вершин, граней, ребер і плоских кутів?Завдання

Многогранник має 12 ребер. Скільки в нього плоских кутів?За мал.1 назвіть елементи многогранника. Що зображено на мал.2?Завдання:мал.1мал.2

Правильні многогранники

Всі правильні многогранники були відомі у стародавній Греції. Їм присвячена заключна 13-а книга знаменитих «Начал». Існує п'ять унікальних форм.Їх називають Платоновими тілами. Платонові тіла

Сьогодні ми ознайомимося із правильними многогранниками, їх видами та цікавими фактами про них. По- грецьки вони закінчуються на едр (edrа-грань), і мають назви: Правильні многогранники

Теорема Ейлера дає відповідь на запитання які і скільки правильних многогранники може існувати?Не існує правильного многогранника, гранями якого є правильні многокутники, якщо число їх сторін більше рівне шість. Тільки правильні трикутники, чотирикутники і п'ятикутники можуть бути гранями правильного многогранника. Теорема Ейлера

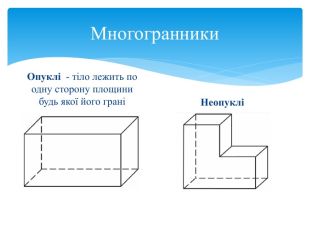
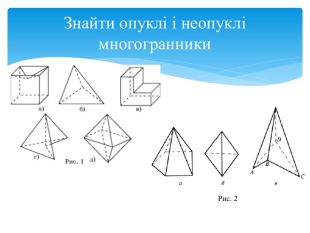
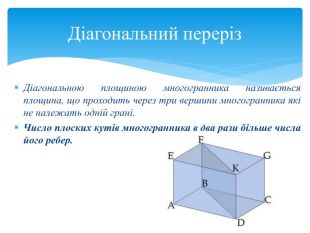
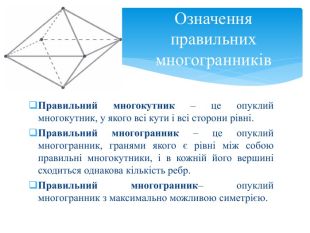
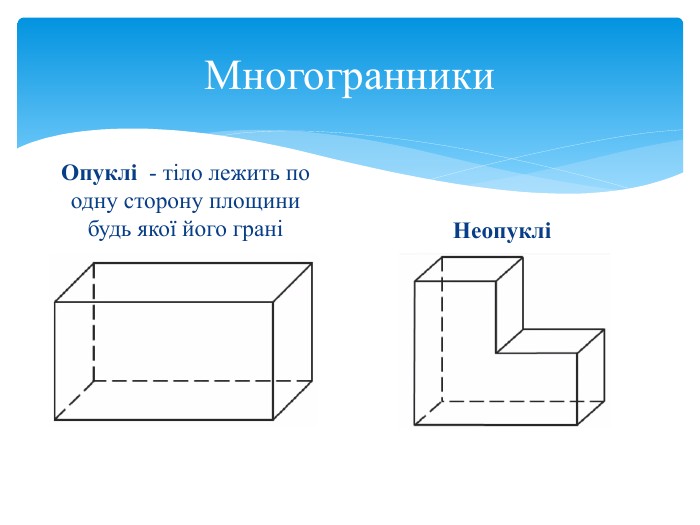
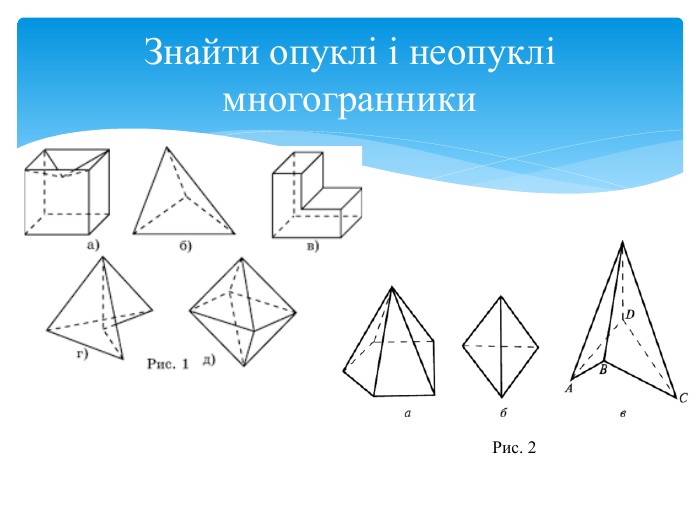
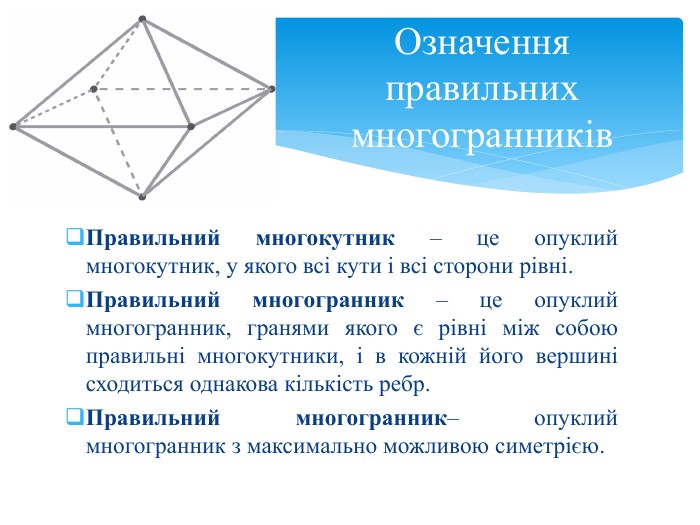
Правильний многокутник – це опуклий многокутник, у якого всі кути і всі сторони рівні. Правильний многогранник – це опуклий многогранник, гранями якого є рівні між собою правильні многокутники, і в кожній його вершині сходиться однакова кількість ребр. Правильний многогранник– опуклий многогранник з максимально можливою симетрією. Означення правильних многогранників

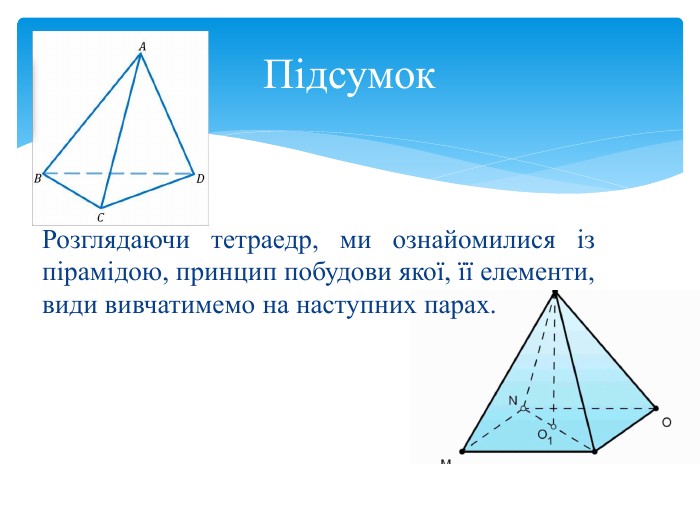
Тетраедр Від «тетра» – чотири і грецького «hedra» – грань. Складається з 4-х правильних трикутників, в кожній його вершині сходяться 3 ребра. Сума плоских кутів при кожній вершині дорівнює 3*60=180 Має 4 грані, 4 вершини і 6 ребер. Тетраедр символізував вогонь, так як його вершина напрямлена вгору. ТЕТРАЕДР – ВОГОНЬ

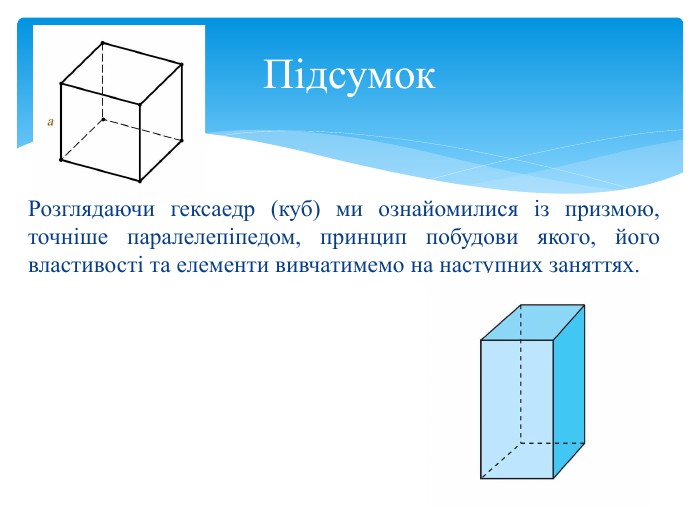
Від грецького «гекса» – шість і «hedra» - грань. Має шість квадратних граней, в кожній його вершині сходяться 3 ребра. Сума плоских кутів при кожній вершині дорівнює 3*90=270 Має 6 граней, 8 вершин і 12 ребер. Гексаедр більш відомий як куб. ГЕКСАЕДР - ЗЕМЛЯ, так як «найстійкіший»Гексаедр (куб)

Від грецького «okto» - вісім і «hedra» - грань. Має 8 граней (трикутники)В кожній вершині сходяться 4 ребра. Сума плоских кутів при кожній вершині дорівнює 4*60=240 Має 8 граней, 6 вершин, і 12 ребер. Октаедр символізує повітря, як «найповітряніший»ОКТАЕДР - ПОВІТРЯОктаедр

Від грецького «eikosi» - двадцять і «hedra» - грань. Має 20граней (трикутних)В кожній вершині сходиться 5 ребер. Сума плоских кутів при кожній вершині дорівнює 5*60=300 Має 20 граней, 12 вершин і 30 реберІкосаедр символізує воду, так як він «обтічний»ІКОСАЕДР - ВОДА Ікосаедр

Від грецького «dodeka» - дванадцять і «hedra» - грань. Має 12 граней (п'ятикутники)В кожній вершині сходяться 3 ребра. Сума плоских кутів при кожній вершині дорівнює 3*108=360 Має 12 граней, 20 вершин і 30 ребер. Додекаедр втілює в собі все суще, символізує все світотворення, вважався головним. ДОДЕКАЕДР - ВСЕСВІТ Додекаедр

Знайти площу розгортки тетраедра і гексаедра з ребром 8 см. Завдання

Розглядаючи тетраедр, ми ознайомилися із пірамідою, принцип побудови якої, її елементи, види вивчатимемо на наступних парах. Підсумок

Розглядаючи гексаедр (куб) ми ознайомилися із призмою, точніше паралелепіпедом, принцип побудови якого, його властивості та елементи вивчатимемо на наступних заняттях. Підсумок

Розв'язування будь-яких стереометричних задач зводиться до планіметрії, в більшості - до співвідношень у прямокутному трикутнику. Запам'ятай!

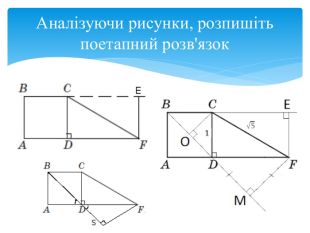
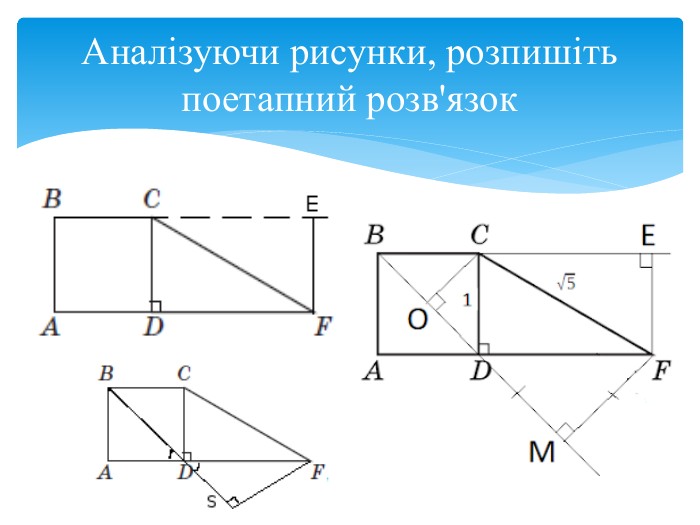
Завдання ЗНОЗавдання: На рисунку зображено квадрат ABCD зі стороною 1 см та прямокутний трикутник CDF, гіпотенуза якого CF дорівнює √5см. Фігури лежать в одній площині. Знайти:1. Довжину катета FD трикутника CDF.2. Довжина радіуса кола, описаного навколо квадрата ABCD.3. Відстань від точки F до прямої BC.4. Відстань від точки F до прямої BD 

Аналізуючи рисунки, розпишіть поетапний розв'язок

Надіюся, що сьогоднішнє заняття відкрило зовсім нове бачення многогранників, правильних многогранників та переконало, що математика є одним із напрямків пошуку істини та просторових відношень.І все ж таки краса світу залежить від математики)Дякую за увагу)