РОЗДІЛ 3  РОЗВ’ЯЗУВАННЯ ЗАДАЧ ПІДВИЩЕНОГО РІВНЯ

 

1. Задача [13]

Сторони паралелограма дорівнюють a і b(ab). Із середини більшої сторони паралельну сторону видно під кутом α. Знайдіть площу паралелограма.

Розв’язання.

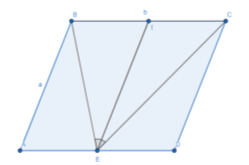
E- середина сторони AD паралелограма ABCD, AD=b, AB=a, а (рис. 61)

Проведемо ET AB.

ET=AB=a.

S_∆BTE = S_∆ABE і S_∆TCE = S_∆ECD

Тому площа паралелограма

S=2 S_∆BEC=BEEC (*)

ET - медіана BCE, тоді

Звідси         

У ∆BEC за теоремою косинусів:

Звідси   BE . Підставляючи це в (*), маємо

S=

Відповідь:

2. Задача Відношення периметра ромба до суми його діагоналей дорівнює k. Знайти кути ромба і допустимі значення k.

Розв’язання

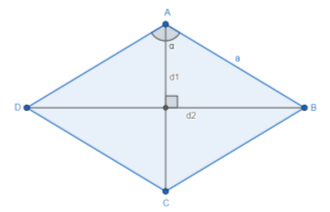
Нехай d₁ i d₂ – діагоналі ромба, а – сторона ромба. (рис. 62)

 

За умовою , тобто

Крім того, (використовуючи властивість діагоналей паралелограма). Виразимо двічі площу ромба:

Де α- гострий кут ромба. Звідси

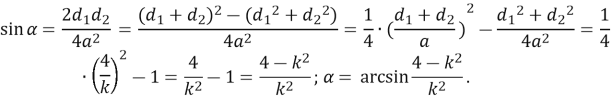
Оскільки , то

Враховуючи маємо

Зрозуміло, що другий кут ромба дорівнює

Відповідь: і , де

3. Задача Діагональ прямокутника дорівнює d  і  ділить кут прямокутника у відношенні m:n.Знайти периметр прямокутника.

Розв’язання

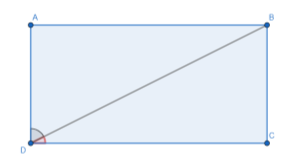
Позначимо ADB=mx;

  

∠BDC=nx. Тоді mx+nx= і .

Маємо ∠ADB= ∠BDC =

Шуканий периметр

P=2d() =

=

=

Відповідь:.

4. Задача Відношення площі прямокутника ABCD (BCǁAD) до квадрата його діагоналі дорівнють k. Знайти кут EAF, де E і F – відповідно середини сторін ВС і CD.

Розв’язання

Нехай AB=a, AD=b- сторони прямокутника. Тоді квадрат діагоналі . (рис. 64)

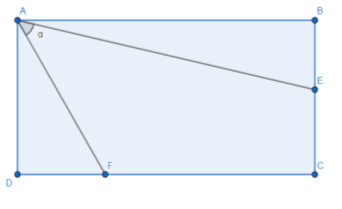
Рисунок 64

За умовою .

Маємо 

Позначемо шуканий кут ∠EAF=α. Тоді 

Візьмемо функцію тангенс від обох частин рівняння, що є гострим кутом:

DAF+∠EAF)

Враховуючи   і формулу

Маємо, .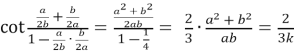

Тоді i(враховуючи 0)

Відповідь: .

5. Задача У квадрат вписано другий квадрат, вершини якого лежать на сторонах першого, а сторони утворюють зі сторонами першого кути в 60⁰. Яку частину площі даного квадрата становить площа вписаного?

Розв’язання

Квадрат  EFGH вписано у квадрат ABCD зазначеним способом. (рис.65)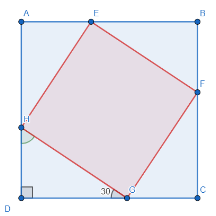

Рисунок 65

Позначимо EF=a. Тобто  DC=DG+CG=. Маємо

 =

Відповідь:

6. Задача У квадраті ABCD Через середину M сторони AB проведено пряму, що перетинає протилежну сторону CD у точці N. У якому відношенні пряма MN ділить площу квадрата, якщо гострий кут AMN дорівнює

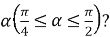
Розв’язання

Оскільки пряма перетинає DC, ф не AD, то обмеження на α маємо такі:

Позначаємо AD=α. Проведемо NK(рис. 66)

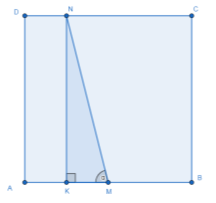
Тоді KM=KN   і DN=AK=AM-KM=

NC=DC-DN=.

Площі чотирикутників DNMA i CNMB знайдемо як площі трапеції. Маємо

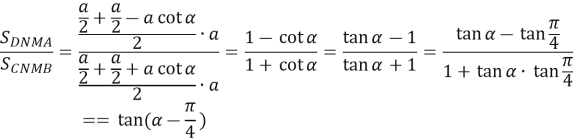
Відповідь:  .

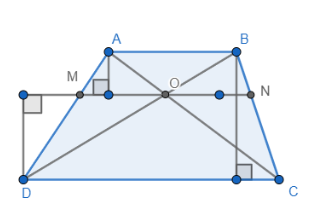
7. Задача Через точку перетину діагоналей трапеції паралельно основам проведено пряму, що перетинає бічні сторони в точках N i M. Довести, що MN=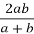,  де a i b – довжини основ.

Розв’язання

Позначимо MO=x. Висоту трикутника AOM позначимо h₁,висоту трикутника OMD позначимо h₂, a висоту трапеції –h. (рис.67)

За умовою AB =a, DC=b. Маємо

∆AMO∆ADC;

∆DMO

(висоти  ∆ADC і ∆DAB також дорівнюють h).

Додаючи отримані рівності, маємо =1; x=

Аналогічно ON=.

Отже, MN=MO+ON=

8. Задача Центр кола, вписаного в прямокутну трапецію, віддалений від кінців її бічної сторони на відстані 3,9 см. Знайти сторони трапеції.

Розв’язання

Нехай точка О- центр кола, вписаного в трапецію ABCD (∠A=∠D=90⁰) OB=3см, OC=9см (рис.68)

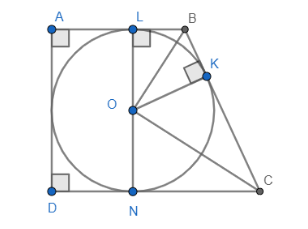
Рисунок 68

Оскільки точка O лежить на перетині бісектрис кутів трапеції, то ∠OBC+∠OCB=∠CBA+∠BCD= ∙(∠CBA +∠BCD)= ∙180⁰=90⁰.

Значить ∠BOC=90⁰. Тоді

BC=

Виразивши двічі площу ∆ OBC, знайдемо OK- висоту цього трикутника й одночасно радіус кола:

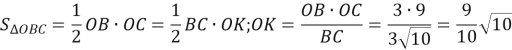
Тоді AD=2r=2∙OK=см. Маємо

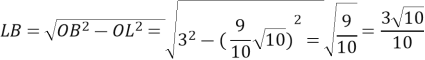
Тоді 

Далі 

Тоді

Відповідь: основи трапеції і см бічні сторони і