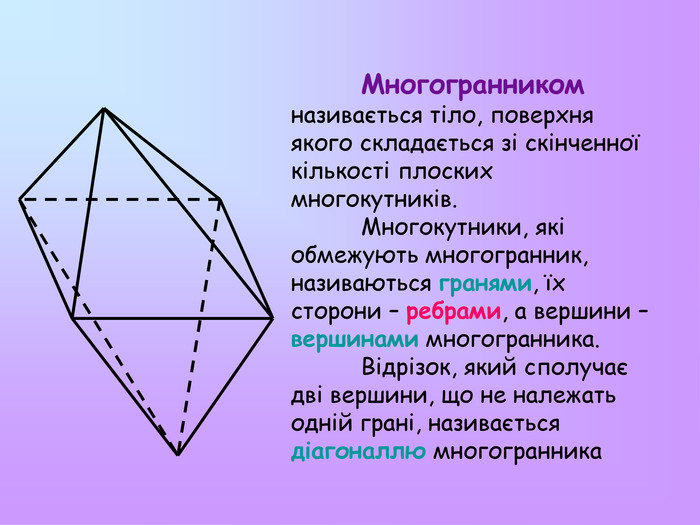
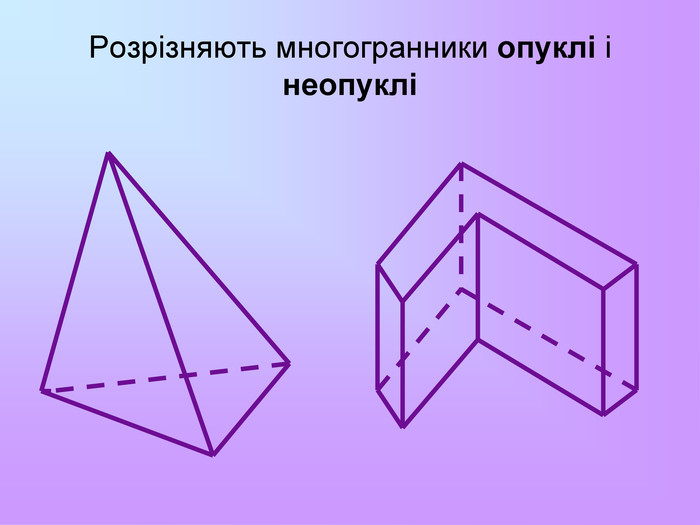
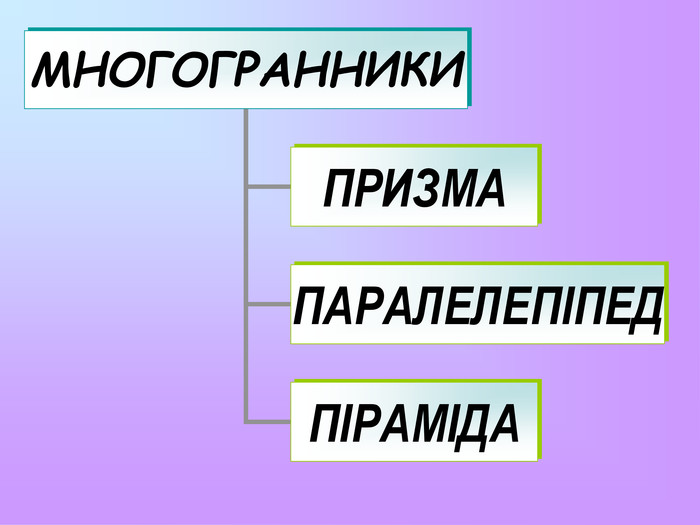
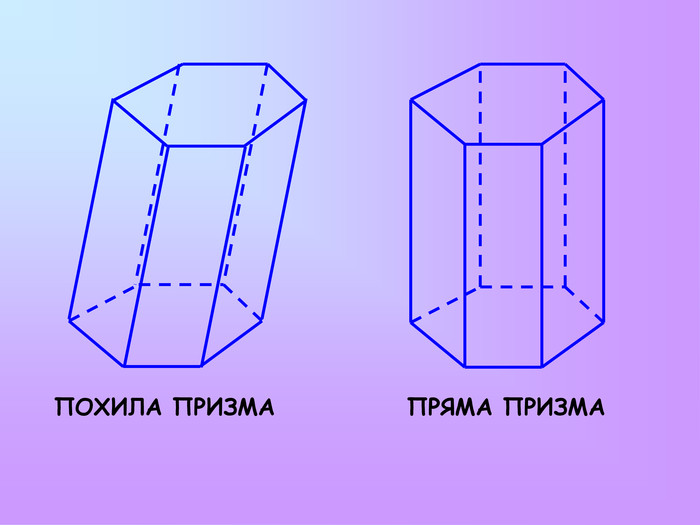
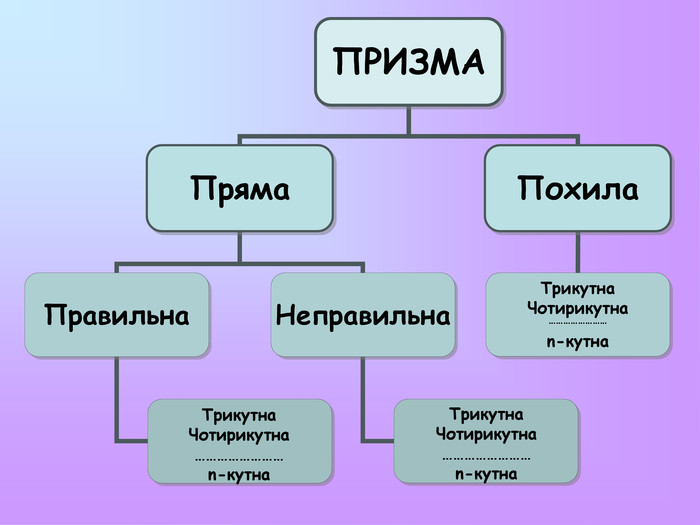
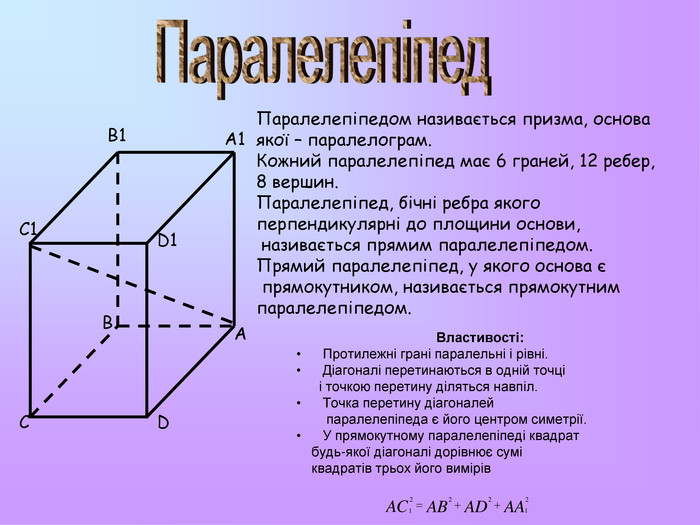
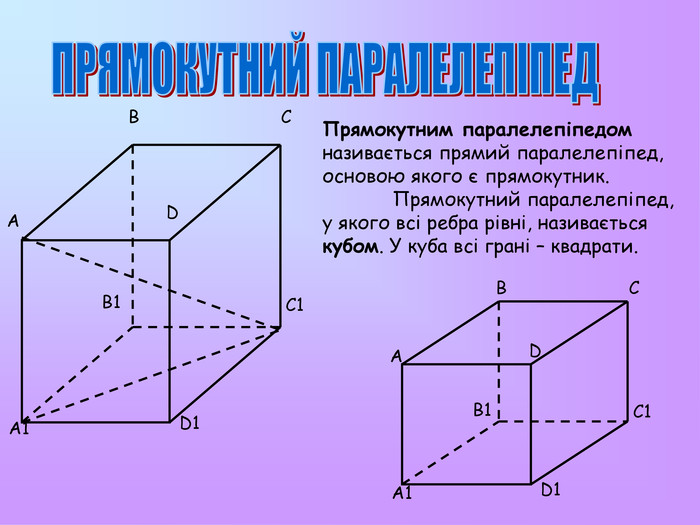
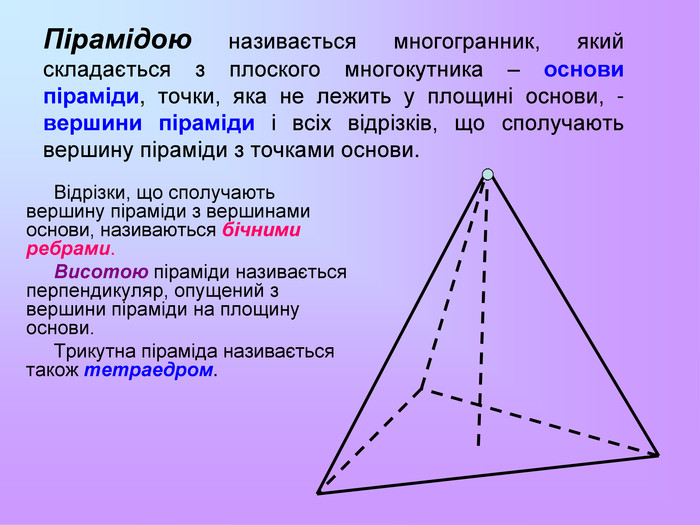
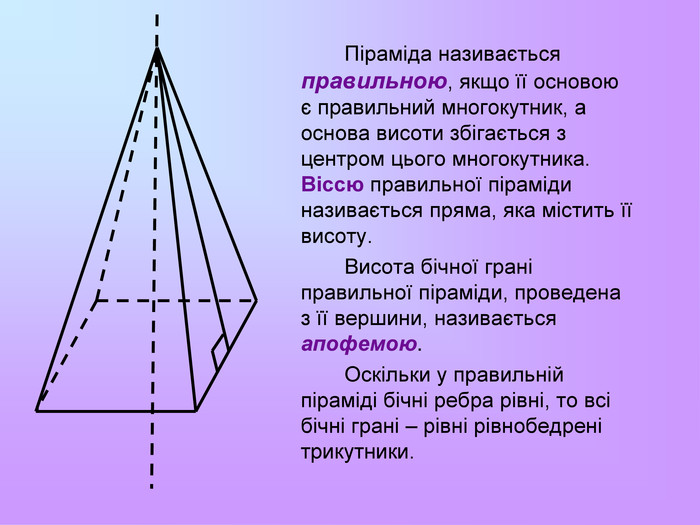
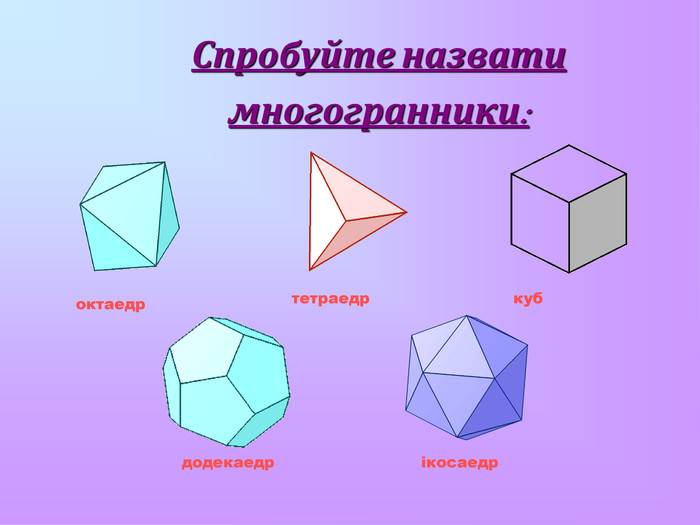
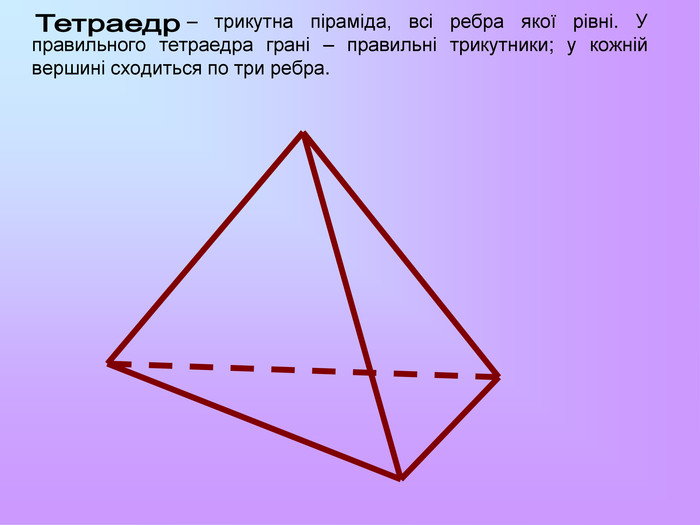
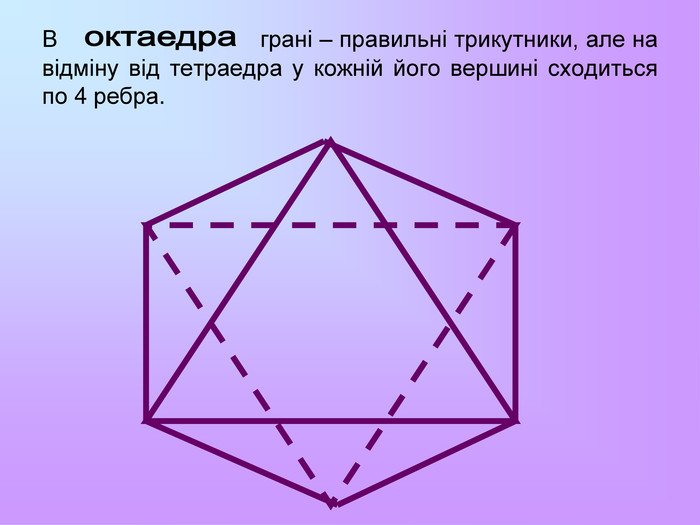
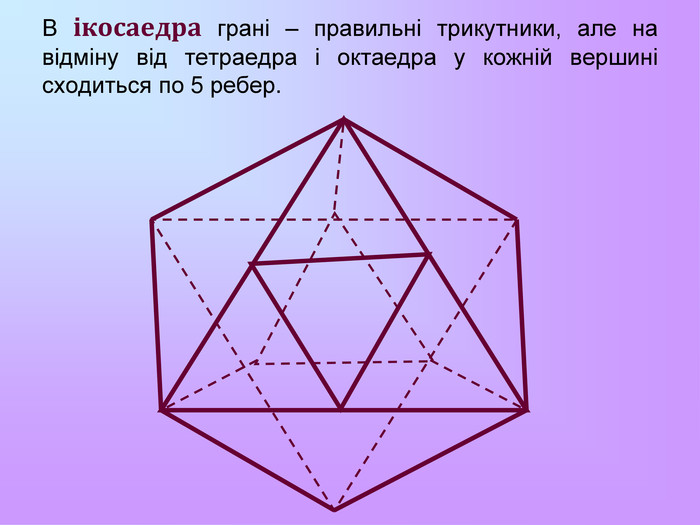
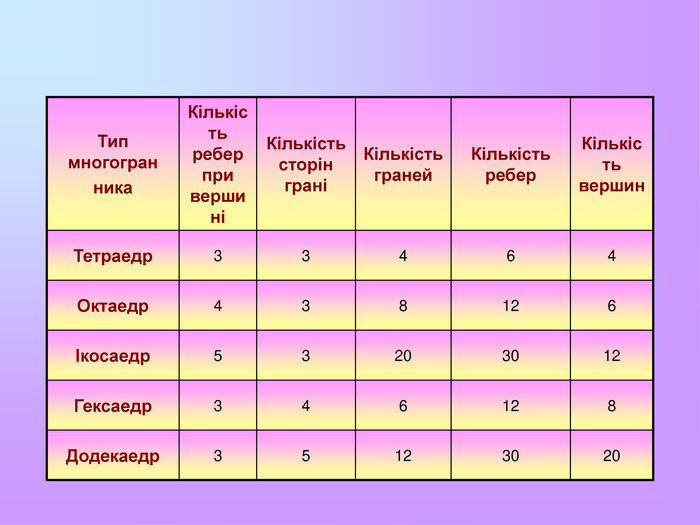
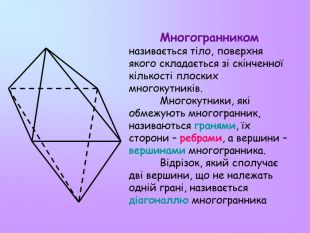
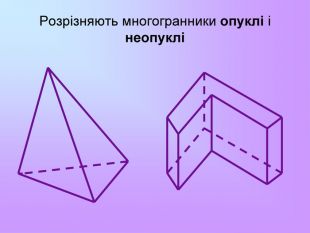
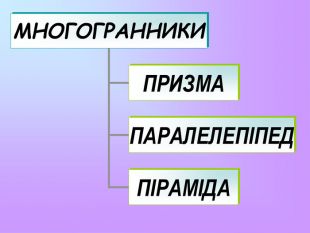
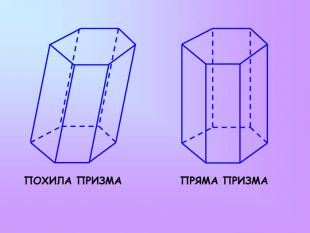
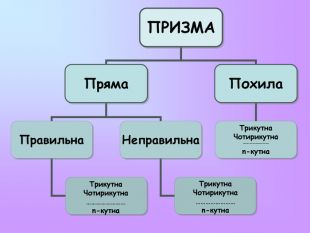
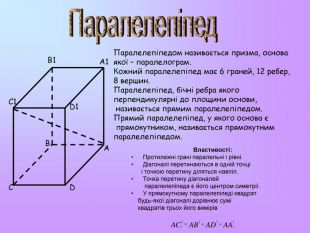
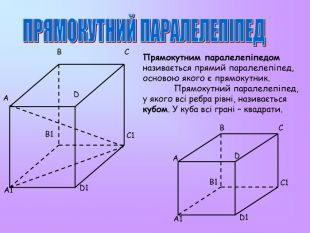
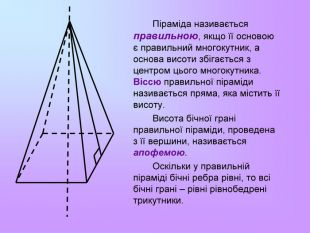
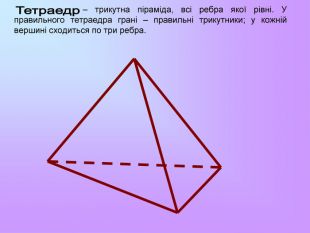
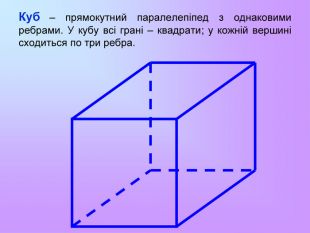
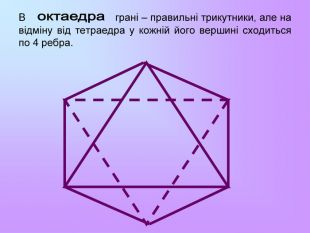
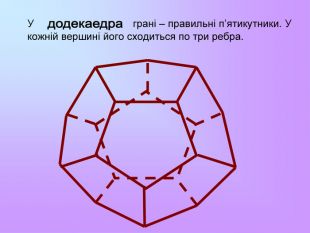
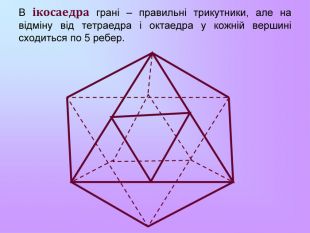
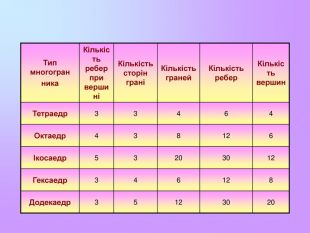
Презентація з математики "Многогранники"
Зміст архіву
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку