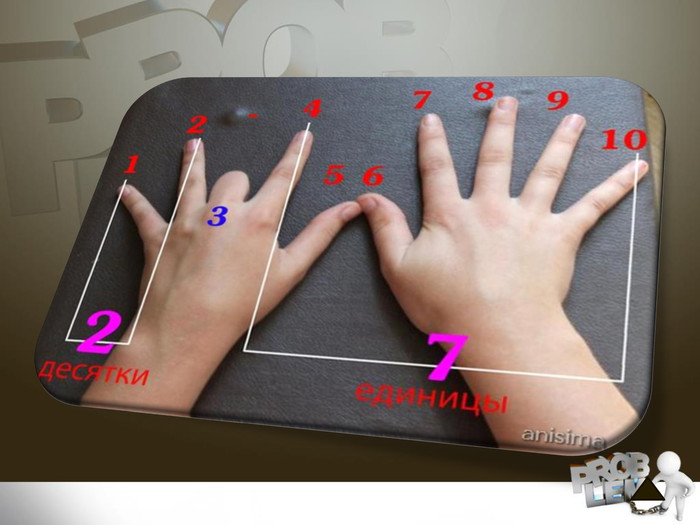
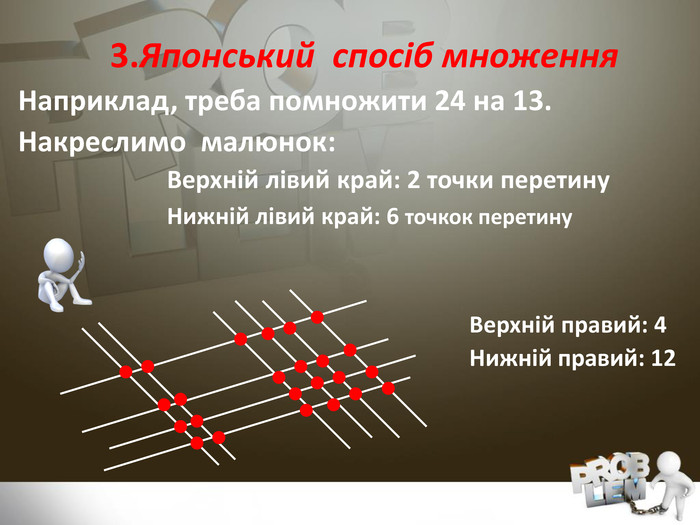
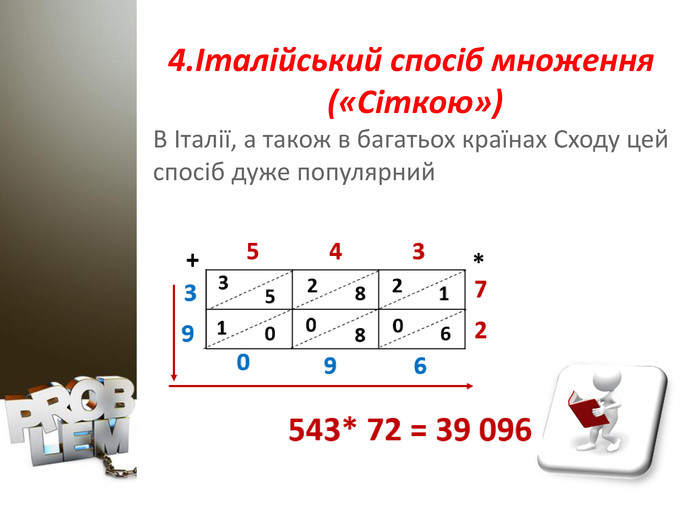
Презентація на тему " Чи існує життя без калькулятора"
Про матеріал
Презентація для позакласного заходу на тему " Чи існує життя без калькулятора"
Для учнів 5-8 класів Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку