Презентація на тему "Функції"
Про матеріал
В презентації викладено теоретичний матеріал з теми, приведені приклади розв'язання вправ та завдання для закріплення розглянутого матеріалу. Презентація допоможе учням систематизувати та узагальнити матеріал з теми "Функції"
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Алгебра і початки аналізу (академічний рівень) 10 клас (Нелін Є.П.)
До уроку
§ 2. Функції Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку




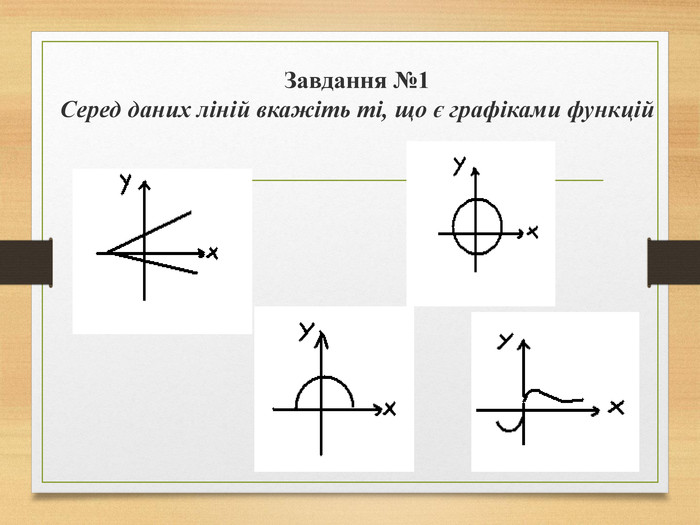
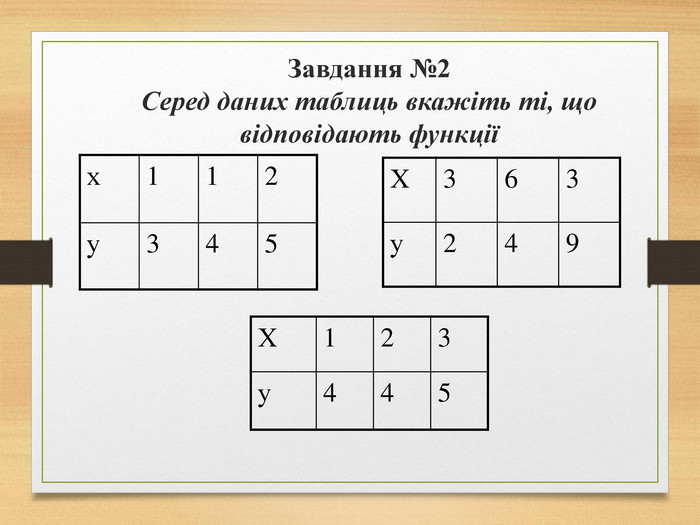


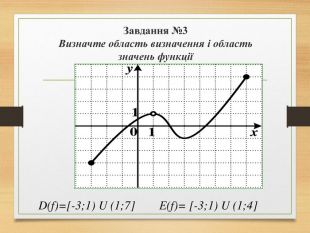
![Завдання №3 Визначте область визначення і область значень функції D(f)=[-3;1) U (1;7] Е(f)= [-3;1) U (1;4] Завдання №3 Визначте область визначення і область значень функції D(f)=[-3;1) U (1;7] Е(f)= [-3;1) U (1;4]](/uploads/files/17980/64796/69276_images/8.jpg)





























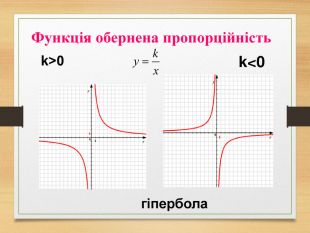
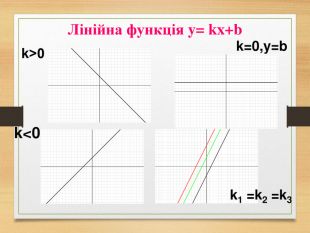
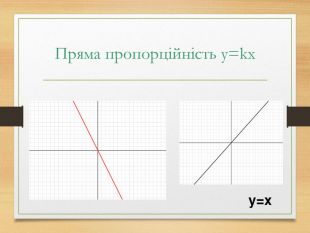
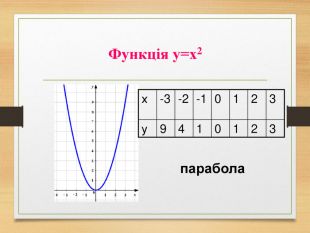
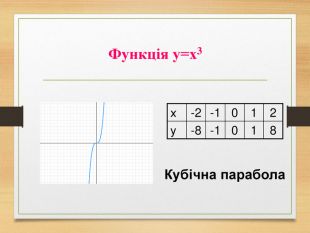
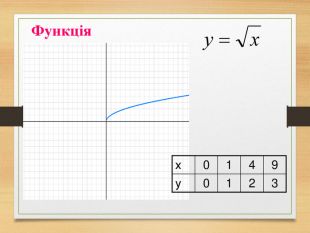



-

Котовський Євгеній
24.03.2025 в 18:00
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гелешко Наталія
12.11.2023 в 00:02
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Перепелиця Тетяна Іванівна
24.09.2023 в 21:37
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ансімова Валентина
09.11.2022 в 08:04
Саме те, що треба. Спасибі велике.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сологуб Ольга Юріївна
27.10.2022 в 18:43
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Інна Сопілка
22.09.2022 в 13:13
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пустовойт Володимир Іванович
21.09.2022 в 12:08
Дякую за допомогу!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дзядевич Наталья
04.09.2022 в 06:13
Чудова презентація. Дуже допомогла. Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Перепелица Анна
04.11.2021 в 15:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Густіліна Юлія Володимирівна
26.09.2021 в 21:41
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Горик Руслана Миколаївна
29.04.2021 в 20:05
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гавриш Світлана Петрівна
27.09.2020 в 22:25
Дякую за змістовну презентацію!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 9 відгуків