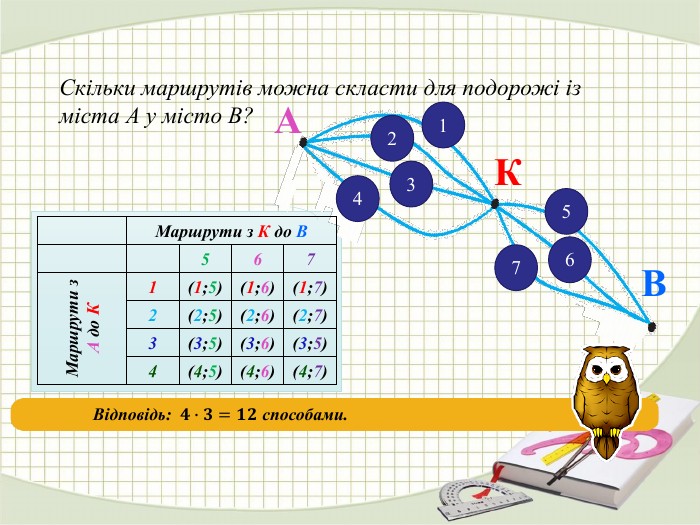
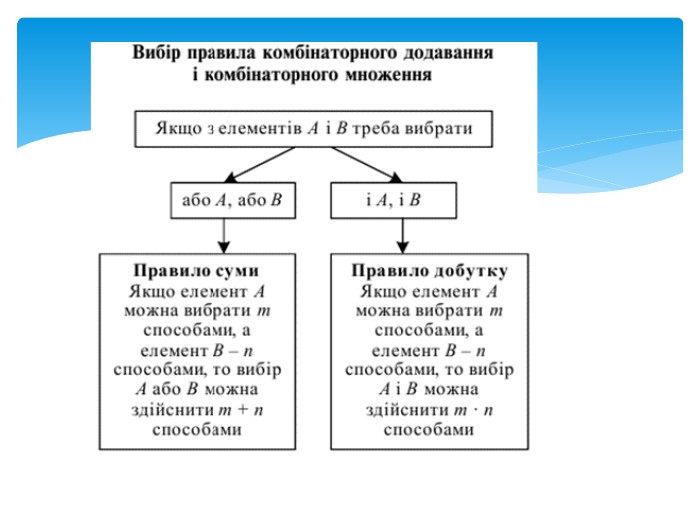
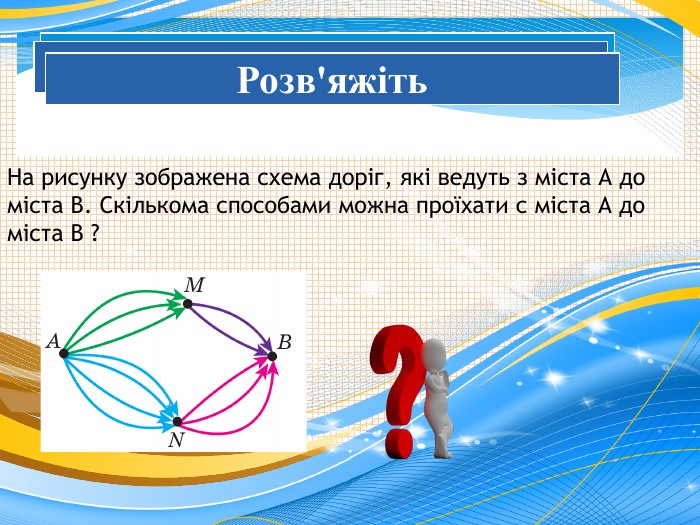
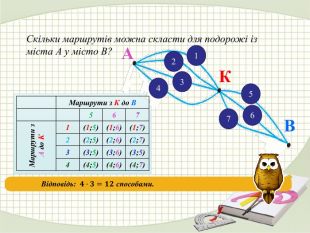
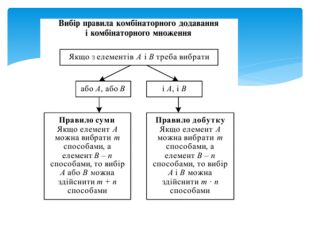
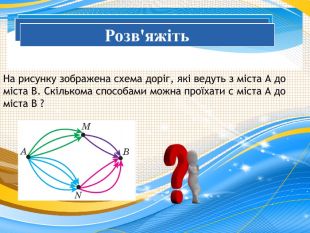
Презентація на тему "Комбінаторика. Комбінаторні правила суми та добутку."
Про матеріал
Презентація дає можливість зробити матеріал наочним. Сформувати комбінаторні правила суми та добутку, а також сформувати у учнів навички їх застосування. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра (академічний, профільний рівень) 11 клас (Нелін Є.П., Долгова О.Є.)
До уроку
21.1. Елементи комбінаторики Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку