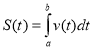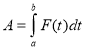Урок "Інтеграл та його застосування"

 

 

 

 

 

МЕТОДИЧНА РОЗРОБКА

Теоретичного заняття з математики

Тема «Визначений інтеграл, його застосування»

 

 

 

 

 

 

Науково - методичне обґрунтування та актуальність теми

 

Виникнення інтегрального числення пов’язане з потребою обчислення площ і об’ємів. Уже в античній математиці для обчислення площ і об’ємів застосовували способи, схожі на обчислення визначних інтегралів. Значних успіхів у цьому досяг давньогрецький математик Архімед (ІІІ до н.е.), який для розв’язування задач на обчислення площ і об’ємів застосовував метод вичерпування (це набір правил для обчислення площ, і обсягів). Криза та занепад древнього світу призвела до забуттю багатьох наукових досягнень. Про методи вичерпування згадали лише у XVII столітті. Це було пов’язано з іменами Ісаака Ньютона, Готфріда Лейбніца, Леонарда Эйлера та інших видатних вчених, які поклали основу сучасного математичного аналізу.

Ісаак Ньютон народився 1643 року. У 1665–1667 роках Ньютон почав працювати над створенням математичного апарату, за допомогою якого можна було б досліджувати й висловлювати закони фізики. Ньютон перший побудував диференціальне і інтегральне обчислення (методом флюксій). Це дозволило вирішувати найрізноманітніші математичні і фізичні завдання.

Готфрід Вільгельм Лейбніц народився у Німеччині 1646 р. В кінці XVІІ ст.           Г. Лейбніц, незалежно від І. Ньютона, розробив для операцій диференціювання та інтегрування системи позначень і правил, вказав на зв’язок між ними. З того часу це окремий розділ математики. Метод Ньютона – Лейбніца починається заміною кривої, що обмежує площу, яку потрібно знайти, послідовністю ламаних, що наближається до неї, аналогічно до методу вичерпування.

У XVІІІ ст. розвитку інтегрального числення найбільш сприяли праці Якоба та   П. Бернуллі, Ж Лагранжа і особливо Ейлера, який довів апарат інтегрального числення майже до сучасного стану.

 

Основні вимоги

     У результаті вивчення теми студенти повинні

Знати:

• Визначення визначеного інтеграла;
• Таблицю первісних
• Правила знаходження інтегралів;
• Геометричний та фізичний зміст інтеграла;
• Формулу для обчислення площі криволінійної трапеції;

Вміти:

• Знаходити первісні функцій;
• Знаходити загальний вигляд первісної, що проходить через точку;
• Застосовувати правила інтегрування до розв’язування задач; 
• Розв’язувати задасі на знаходження площі криволінійної трапеції;
• Розв’язувати нескладні прикладні задачі на використання визначеного інтеграла;

Міжпредметна інтеграція

 

Забезпечуючі	Знати	Вміти
Геометрія Тема: «Знаходження площі фігури обмеженої графіками функцій»	Формулу для знаходження площі, обмеженої графіками	Будувати графіки елементарних Визначати який лежить вище, а який нижче Обчислювати за формулою визначений інтеграл
Фізика Знаходження шляху за даним рівнянням швидкості; Знаходження роботи за прикладеною силою;	Тема: Механіка Тема: Термодинаміка	Знаходити визначені інтеграли, вміти використовувати правила для обчислення визначених інтегралів
Біологія Обчислення площ суцвіття квітки	Популяція, швидкість розмноження популяції, суцвіття, види суцвіть	Знаходити визначені інтеграли
Хімія Швидкість зміни концентрації речовини	Хімічний зміст визначеного інтеграла	Обчислювати швидкість зміни концентрації речовини
Економіка Знаходження капіталу, за основними інвестиціями; Витрата бензину в залежності від швидкості	Продуктивність, споживач, надлишок	Знаходити визначені інтеграли

 

Математика – потужна зброя в руках фізика, економіста, біолога, еколога.  Адже багато наслідків можна одержати математично, використовуючи перевірені дослідом формули. Зараз ваші однокласники покажуть, як використовуючи цю зброю, вони виконали своє завдання.

Давайте розглянемо, чи зможе нам  знадобитися визначений інтеграл при розв’язуванні задач з інших предметів.

Задачі фізики.

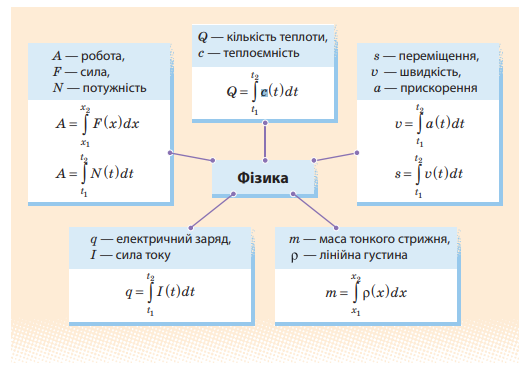
Фізичний зміст інтегралу полягає в тому, щоб знайти шлях, який долає  фізичне матеріальне тіло за певний проміжок часу.

Розглянемо одну з задач ЗНО.

 Задача 1. Нехай  швидкість тіла υ з часом t змінюється за наступним законом:  

υ =20-3t. Знайти шлях, що пройшло тіло за четверту секунду свого руху.

  Розв’язання:

υ(t) = , тоді

За четверту секунду

 

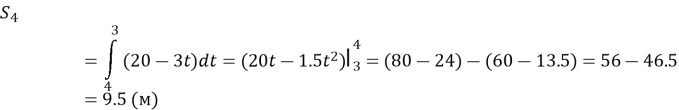
Задача 2. (Про електроенергію)

Сила струму в провіднику з часом змінюється за законом . Яка кількість електрики пройде через поперечний переріз провідника за час від третьої до шостої секунди?

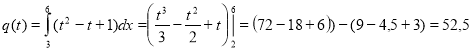(Кл)

Задачі економіки.

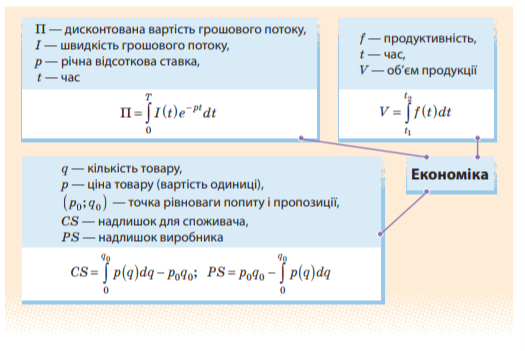
Задача 3. Розглянемо задачу знаходження капіталу (основних фондів) за відомими чистими інвестиціями . Чисті інвестиції (капіталовкладення)- це загальні інвестиції, які були зроблені за певний проміжок часу, за винятком інвестицій на відшкодування основних фондів (капіталу), які виходять з ладу. Таким чином, за одиницю часу капітал збільшується на суму чистих інвестицій.

Якщо капітал розглядати як функцію часу , а чисті інвестиції, відповідно, як , то викладене вище можна записати у вигляді:

.

Часто вимагається знайти приріст капіталу за період з моменту часу до , тобто величину . Враховуючи, що - первісна для функції , маємо:

.

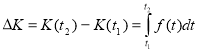Задача 4. .  Чисті інвестиції задано функцією .

Визначити:

а) приріст капіталу за три роки;

б) термін часу (у роках), після якого приріст капіталу складає 50000.

Розв’язок. а) Скористаємося формулою для обчислення , врахувавши, що = К(3) – К(0),

поклавши =0; =3.

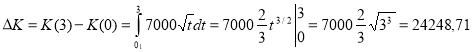- приріст капіталу за три роки.

б)Дізнаємося термін, коли приріст капіталу складатиме 50000. Позначимо шукану тривалість часу через Т, тоді

.

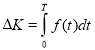Підставляємо і .

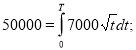
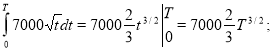
Ще одна з економічних проблем нашого сьогодення – це дороге паливо. Нас теж зацікавило це питання

Задача 5. Експериментально встановлено, що залежність витрати бензину автомобілем від швидкості на 100 км шляху визначається формулою
Q = 18 – 0,3v + 0,003v², де 30  v  110. Визначити середню витрату бензину при швидкості руху 50-60 км/год.

Розв’язання

Середня витрата бензину становить

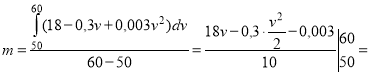
(л).

Отже, автомобіль на 100 км шляху, рухаючись зі швидкістю 50-60 км/год, витрачає в середньому 10,6 л бензину. А це, погодьтеся, не малі гроші.

Задача 6. З інтернету ми дізналися, що навантаження    на   Ташлицьку теплоелектростанцію     задається     функцією   

f(x) = 3x² + 4x – 2. Визначити витрати електроенергії протягом доби.

Розв’язання:

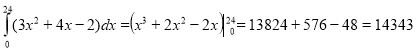( кВт·год)

Відповідь: 14343 кВт·год.

І це тільки на одній станції, уявіть яка кількість електроенергії по всій Україні!

Задачі екології.

На деяких уроках ви  також знайомилися з наслідками діяльності людини і факти проти людини. Подивимося  відео  на, якому познайомимося  з екологічною проблемою.

Відео «Мусорная свалка в Тихом океане»

  Із 50-х років у всьому світі почався стійкий ріст інтересу до використання математики в екології.

Задача 7. Визначити розміри сміттєвого острову. Знайти площу сміттєвого острову.

Розв’язання. Острів не має певної геометричної форми. Але можна використати формулу Ньютона - Лейбніца  до обчислення площі криволінійної трапеції.   Якщо проаналізувати форму острова та течії, які його створили можна прийти висновку, що за формою він нагадує   трапецію утворену двома параболами, або  двома синусоїдами.

Отже,  обчислимо площу сміттєвого острова, якщо він обмежений лініями:

у= х² ;  у= 2х -х²;     у=0.

( Побудуємо графіки функцій у = х² і у = 2х - х² і знайдемо абсциси то­чок перетину цих графіків із рівнян­ня: х² = 2х – х². Корені цього рівнян­ня х₁ = 0, х₂ = 1. Дана фігура зобра­жена на рис.

 

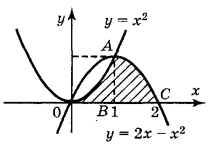Із рисунка видно, що ця фігура складається з двох криволінійних трапецій: ОАВ₁  і  В₁ АС.

Отже, шукана площа дорівнює сумі площ цих трапецій:

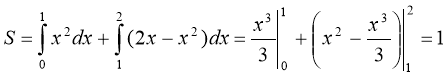
Відповідь: 1кв. од.

Задача 8. Обчислити площу ( а саме товщину)  сміттєвого острова, якщо він обмежений лініями  у = sin x та y = 2 sin x.

S = dx =  dx= - cos х = - (-1-1) = 2 кв.од.

Відповідь: 2 кв. одиниці.

Задачі хімії та біології.

Задача 9.  Швидкість зміни концентрації речовини, що вступила в реакцію, виражається функцією v = 3t + 1, де t – час (с), v – швидкість (моль/см³). Як зміниться концентрація речовини за час t₁=0 до t₂ =5 c?

Розв’язання

Задача розв’язується методом безпосереднього інтегрування. Оскільки v(t)=C ' (t) ,то C(t) – концентрація речовини і первісна для v(t), тому

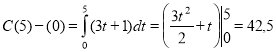(моль/м³). Тобто, якщо використати таку концентровану речовину, яка б змогла знешкодити цей острів, то це можна було б здійснити  за декілька років.

Задача 10.  Покажемо, що інтеграл можна застосовувати і для обчислення площі квітки. Ось вам завдання:

Знайти площу пелюстки ромашки, яка розміщена  між дугами парабол у=х² та у=.

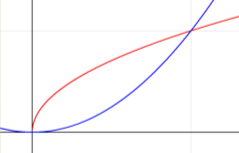
Дана фігура обмежена графіками двох функцій: у=х² та у=. Шукана площа за допомогою інтеграла обчислюється так:

S = 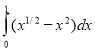= = 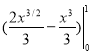– = (кв. од.)

Відповідь. кв. од.

А ще мене зацікавило питання: а чи зможу я обчислити об’єм тіла, утвореного в результаті обертання моєї пелюстки?

Застосовуємо формулу V= , маємо:

V =  

= ( ) = ( куб. од.)

Застосування інтеграла у домогосподарстві.

 

 

Задача 11. Акваріум має форму прямокутного паралелепіпеда. Знайти силу тиску води (густина води 1000 кг/м³), яка наповнює акваріум, на одну з його вертикальних стінок, розміри якої 0,4 х 0,7 м.

Розв’язання. Візьмемо систему координат так, щоб осі Оу і Ох відповідно містила верхню основу і бічну сторону вертикальної стіни акваріума. Щоб знайти силу тиску, скористаємось формулою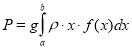 

Стінка має форму прямокутника, тому . Оскільки межі інтегрування a=0 i b=0,4, то дістанемо

.

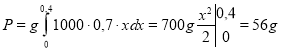Враховуючи, що м/с² , маємо

Отже, сьогодні на уроці ви переконалися в тому, наскільки багатогранним є застосування визначеного інтеграла, а математичні теорії є надійним знаряддям в розкритті таємниць природи, законів економічних, хімічних, біологічних та інших процесів. Для розв’язування цілого ряду задач математики було створено багато спеціальних варіацій поняття інтеграла таких як: кратні, криволінійні, поверхневі інтеграли і т.і. З ними ви ознайомитесь в курсі вищої математики. А зараз на закінчення я пропоную вам відгадати кросворд:

 

Домашнє завдання: продовжувати опрацьовувати матеріали ЗНО