Урок алгебри в 11 класі « Комбінаторика. Сполуки без повторень: перестановки, розміщення, комбінації »

Про матеріал

Познайомити учнів із сполуками без повторень, ввести поняття «комбінаторні задачі», розглянути групи сполук (перестановки, розміщення, комбінації), навчити встановлювати зв'язок між теоретичними знаннями та практичною діяльністю.

Перегляд файлу

УРОК АЛГЕБРИ І ПОЧАТКІВ АНАЛІЗУ В 11 КЛАСІ

Тема уроку : Комбінаторика. Сполуки без повторень: перестановки, розміщення, комбінації (пара)

Тип уроку: засвоєння нових знань

Мета уроку:

Навчальна: познайомити учнів із сполуками без повторень, ввести поняття «комбінаторні задачі», розглянути групи сполук (перестановки, розміщення, комбінації), навчити встановлювати зв'язок між теоретичними знаннями та практичною діяльністю.

Формування умінь та навичок: вчити розв’язувати найпростіші комбінаторні задачі, використовуючи формули сполук та правила суми та добутку, розвивати логічне мислення, пізнавальний інтерес до даної теми і предмету математики зокрема, формувати навички роботи в парах, розвивати вміння співвідносити теоретичний матеріал з практикою.

Виховна: виховувати уважність, відповідальність за спільний результат, усвідомлення необхідності отримання знань для застосування в подальшому навчанні.

Ключові компетентності: спілкування державною мовою — чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень; основні компетентності у природничих науках і технологіях — розпізнавати проблеми, що виникають у довкіллі і які можна розв’язати засобами математики; вміння вчитися впродовж життя — прагнути до вдосконалення результатів своєї діяльності.

Навчально-методичне забезпечення уроку: Матеріали інтернет-ресурсу, комп’ютер, проектор, екран, мультимедійна презентація, опорний конспект, тестове завдання.

Хід уроку:

І. Організаційний момент

Перевірка наявності учнів на уроці та налаштування їх на роботу.

ІІ. Актуалізація опорних знань

Перевірка домашнього завдання:

Що ми називаємо факторіалом?

Факторіал – це добуток натуральних чисел від 1 до n, який позначається n!

Як знайти факторіал: 2!; 5!; 6!; (n + 1)!
Скоротити дріб: ; ;

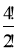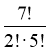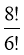
Розв’язання: = = 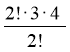12

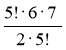= = 7 · 4 = 28

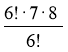= = 56

Дати означення правила суми та навести приклади.

Якщо деякий елемент множини А можна вибрати n способами, а елемент множини В – m способами, то вибір елемента із множини А або із множини В можна зробити n + m способами.

Наприклад: У коробці 5 олівців і 7 фломастерів. Скількома способами можна вибрати один олівець або один фломастер?

Розв’язання: Один олівець можна вибрати 5 способами, а один фломастер 7 способами. За правилом суми, один предмет можна вибрати 5 + 7 = 12 способами.

Дати означення правила добутку.

Якщо якийсь елемент множини А можна вибрати n способами, а із множини В – m способами, то пару елементів можна вибрати n · m способами.

Наприклад: У коробці 5 олівців і 7 фломастерів. Вибрати пару, яка складається з одного олівця та одного фломастеру.

Розв’язання: Один олівець вибираємо 5 способами, а один фломастер – 7 способами. Отже, для того щоб вибрати пару, необхідно 7 · 5 = 35 способами.

ІІІ. МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ

Що ж таке сполуки без повторень?

Це скінчені множини, які складаються з елементів або об’єктів будь - якої природи, та їх підмножини. Це можуть бути які - небудь окремі предмети або живі істоти - люди, звіри, гриби, рослини, і т. д., при цьому нас зовсім не цікавить із чого множина складається, головне, що ці об’єкти піддаються підрахунку і їх три: перестановки, розміщення, комбінації.

Представникам різних професій доводиться розв’язувати задачі, в яких із деякої множини об’єктів потрібно вибрати елементи, що містять ті або інші властивості, розміщувати ці елементи в певному порядку. Так, керівнику цеху потрібно розподілити кількість видів роботи між працівниками, агроному – розмістити посіви на кількох полях і т. д.

Оскільки в таких задачах йде мова про комбінування об’єктів, їх називають комбінаторними задачами, а розділ математики – комбінаторикою.

ІV. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

Історія виникнення комбінаторики :(презентація учнів)

Комбінаторика - важливий розділ математики, знання якого необхідно представникам різноманітних спеціальностей. З комбінаторними задачами доводиться мати справу фізикам, хімікам, біологам, лінгвістам, спеціалістам по кодам та ін. Комбінаторні методи лежать в основі рішення багатьох задач теорії ймовірностей та її застосувань.

Комбінаторика - гілка математики, що вивчає комбінації та перестановки предметів, - виникла в XVII ст.

Зараз комбінаторні методи застосовуються в теорії випадкових процесів, статистиці, математичному програмуванні, обчислювальній математиці, плануванні експериментів і т. д.

Справи давнини.

З задачами, в яких приходиться вибирати ті чи інші предмети, розміщувати їх в певному порядку і відшуковувати серед різних розміщень найкращі, люди зіткнулися ще в доісторичну епоху, обираючи найкращі розміщення мисливців під час полювання, воїнів під час битви, інструментів під час роботи. Певним чином розміщувалися прикраси на одязі, візерунки на кераміці. З ускладненням виробничих і суспільних відносин ширше приходилося користуватися загальними поняттями про порядок, ієрархію, групування. В тому ж напрямку діяв розвиток ремесел, торгівлі.

Комбінаторні навички виявилися корисними і в години дозвілля. Не можна точно сказати, коли поряд із змаганнями по бігу, метанню диску, стрибках з’явились ігри, що потребували в першу чергу вміння розраховувати, складати плани і спростовувати плани противника.

Перша згадка про питання, близькі до комбінаторних, зустрічається в китайських рукописах, що відносяться до XII – XIII ст. до н.е.

Пізніше з’явились нарди, шашки й шахмати, а також їх різноманітні варіанти (китайські та японські шахи, японські облавні шашки „го” і т. д.). В кожній з цих ігор доводилося розглядати різноманітні комбінації фігур, що мали здатність пересовуватись, та вигравав той, хто їх краще вивчив, знав переможні комбінації та вмів уникати програшів.

Серед предметів, покладених в піраміду, де 35 століть тому назад був похований єгипетський фараон Тутанхамон, знайшли розкреслену дощечку з трьома горизонталями і 10 вертикалями та фігурки для давньої гри „сенет”.

Комбінаторика в Древній Греції.

Певні уявлення про комбінаторику були і у грецьких вчених. Філософ Ксенократ, що жив в ІV ст.. до. н.е. підраховував кількість складів. В ІІІ ст. до н.е. стоїк Хрисипп вважав, що кількість тверджень, які можна отримати з 10 аксіом, перевищує мільйон. На думку Геппарха, із стверджуючих аксіом можна скласти 103 049 сполучень, а, додавши до них заперечні, 310 95.

Конкретні комбінаторні задачі, що торкалися перерахунку невеликих груп предметів, греки розв’язували без помилок.

Комбінаторика в країнах Сходу.

В VIII ст. н.е. почався розквіт арабської науки. Араби переклали багато творів грецьких учених, вивчили їх, а потім просунулись вперед в науці про рішення рівнянь, теорії та практиці обчислень та ін. Вирішуючи питання про знаходження коренів з будь-якого степеня, арабські алгебраїсти вивели формулу для степеня суми двох чисел, яка відома назвою „біном Ньютона”.

Гра в кості.

Значний поштовх до розвитку комбінаторики дали азартні ігри, які існували ще в глибоку давнину, але отримали особливе розповсюдження після хрестових походів. Найбільшу популярність отримала гра в кості - два чи три кубики з нанесеними на них очками кидали на стіл, і вигравав той, хто отримував більшу кількість очок.

Не дивлячись на давнину ігор, в яких застосовувались кості, вони довго не піддавались математичному дослідженню. Але гравці, які без перестану тренувались у киданні костей, помітили, що деякі суми очок випадають часто, а інші - рідко.

Шифри та анаграми.

Не тільки азартні ігри спонукали математиків до комбінаторних роздумів. Ще з давніх давен дипломати, що прагнули до таємних переписів, винаходили все більш складні шифри, а секретні служби інших держав намагалися ці шифри розгадати. Одним з найпростіших шифрів була „тарабарська грамота”, в якій літери замінювались іншими за певними правилами.

Для кодування та розшифрування залучались математики. Ще в кінці XVI ст. розшифруванням переписів між ворогами французького короля Генріха ІІІ та іспанцями займався один із творців сучасної алгебри Франсуа Вієт.

Шифрами користувались не тільки дипломати і заколотники, але й самі вчені.

Ієрогліфи та клинопис.

Навички в розгадці складних шифрів допомогли ученим, коли археологи почали відкопувати каміння та черепи з таємними знаками - писемністю, що замовкла декілька тисячоліть тому. Одним з найкращих успіхів у розшифруванні було читання французьким філологом Жаном Франсуа Шампольним ієрогліфів, якими писали єгиптяни ще до того, як виникла наука у древніх греків.

Це було торжеством комбінаторного методу у читанні забутих письмен, заснованого на спостереженні за текстом, на співставленні повторювання комбінацій слів та граматичних форм у поєднанні з уявою.

Комбінаторика в біології.

Складність будови біологічних систем, їх строга ієрархічність, взаємо поєднання окремих процесів в цілому організмі роблять біологію підхожим полем для прикладення комбінаторних методів.

Біолог А.А. Любищєв припускав навіть, що схожість рослин та морозних візерунків на вікнах не випадкова - в обох випадках прослідковуються певні закони комбінування частин в одне ціле.

Однією з найбільш складних загадок в біології ХХ ст. була будова „ниток життя” - молекул білка і нуклеїнових кислот. Виявилося, що молекули білка – це об’єднання декількох довгих ланцюгів, що складалися з 20 амінокислот.

Найбільшим досягненням комбінаторного підходу до проявів життя можна вважати розшифровку будови дезоксирибонуклеїнової кислоти (ДНК)

Хімічний пасьянс.

17 лютого 1869 р.- у цей день з хаосу хімічних елементів, кожен з яких мав свої властивості, виникла таблиця - був відкритий періодичний закон. Це відкриття було зроблено Дмитром Івановичем Мендєлєєвим.

Мендєлєєв спробував піти забороненим шляхом, групуючи схожі елементи один з одним. Він зробив і наступний, найскладніший крок, спробував розмістити в правильному порядку і групи.

Як писав пізніше сам Дмитро Іванович: „шукати щось, хоча б гриби, чи якусь залежність, не можна інакше, як дивлячись та пробуючи”. Для того щоб „дивитися і пробувати”, він почав підбирати, написавши на окремих картках назви елементів з їхніми атомними масами та властивостями даного елемента, схожі елементи та атомні маси.

Розкладуючи свій хімічний пасьянс, великий вчений після напружених роздумів, знайшов правильне розміщення елементів.

Не тільки у відкритті періодичної системи елементів виявилась корисною комбінаторика. Як відомо, серед обмежених об’єднань зустрічаються й ізомери, тобто об’єднання, котрі мають один і той самий склад, але різну будову. Комбінаторика дала можливість перерахувати усі ізомери даного складу.

У фізиці комбінаторика виявляється необхідною при вивчені властивостей кристалів, опису моделі феромагнетизму та ін.

Комбінаторика епохи комп’ютерів.

Зараз на наших очах змінюється співвідношення дискретної та класичної математики. На протязі двох з половиною століть основну роль у вивчені природи грав математичний аналіз – диференціальне та інтегральне числення, диференціальні рівняння математичної фізики, варіаційне числення та ін. Процеси, що мали автоматичну природу, замінювались неперервними, щоб можна було застосовувати до них розвинений апарат математики неперервного. Дискретна математика була Попелюшкою, краса якої затьмарювалась блиском впливових та сильних сестер.

Положення справ змінилося після того, як були створені ЕВМ. Тепер такі абстрактні образи математики, як математична логіка, загальна алгебра, формальні граматики, стали прикладними - для складання алгоритмічних мов, на яких пишуть програми для машин, потрібні спеціалісти саме з цих областей математики. Важливу роль почали відігравати різноманітні схеми, дослідження сітківок та їх властивості.

В цю епоху дискретної математики змінилась і роль давньої області дискретної математики - комбінаторики. З області, що цікавила більшу частину авторів задач та знаходила основні застосування в кодуванні і розшифруванні давніх письмен, вона перетворилася на область, що знаходилась на магістральному шляху розвитку науки. За допомогою ЕВМ стало можливим робити перебори, що раніше потребували сотень і тисяч років.

Отже ,що ж таке комбінаторика?

Комбінаторика - це підрахунок різних комбінацій, які можна скласти із деякої множини дискретних об’єктів.

Потрібно відмітити, що комбінаторика є самостійним розділом математики, і по даній дисципліні написані об’ємні підручники.

Як ми уже знаємо, сполуки - це множини, а без повторень - це множини, які складаються із об’єктів, які не повторюються.

Уявіть, що перед вами на столі з’явилися яблуко, груша, банан.

Перше запитання: скількома способами їх можна розставити?

Отже, ми маємо 6 перестановок.

Але як бути, якщо таких предметів буде більше? Число комбінацій збільшиться.

Друге запитання: скількома способами можна вибрати :

один фрукт;
два фрукта;
три фрукта.

Для подібних задач, які дістали назву комбінаторні, існують загальні методи розв’язання.

Розглянемо їх.

1. ПЕРЕСТАНОВКИ

Будь-яка впорядкована множина, яка складається з n елементів, називається перестановкою з n елементів.

Р = n!

2. РОЗМІЩЕННЯ

Будь-яка впорядкована множина, що складається з m елементів, називається розміщенням із n елементів по m елементів.

${\sf A}_n^m=n(n-1)\dots(n-m+1).$

3. КОМБІНАЦІЯ

Будь-яка множина з m елементів даної множини, що містить n елементів, називається комбінацією з n елементів по m

Властивості:

${\sf C}_n^0=1,{\sf C}_n^n=1,{\sf C}_n^1=n$

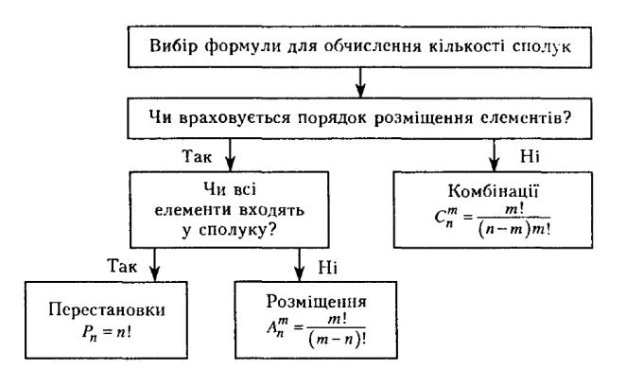
При розв’язуванні задач звертаємо увагу на поняття впорядкованості.

Чи важливий порядок розміщення, чи ні?

Характеристичні ознаки:

Перестановки - предмети різні, порядок важливий, всі місця заняті.
Розміщення - предмети та місця різні, порядок елементів важливий.
Комбінація - предмети різні, порядок вибору не має значення.

Приклади розв’язання:

Скількома способами можна скласти список із дев’яти прізвищ?

Розв’язання: об’єктів 9, n=9, порядок важливий, всі місця заняті, перестановки.

Скільки чотирицифрових чисел можна скласти із запропонованих цифр, не повторюючи їх: 0.1,2,3?

Розв’язання: для того, щоб скласти чотирицифрове число, потрібно використати всі цифри, отже ми отримаємо способи. Коли нуль стоїть на першому місці, то число стає трицифровим, тоді дані комбінації потрібно виключити. Три цифри можна переставити: , маємо 24-6=18 способів.

Скільки різних двоцифрових чисел можна скласти із запропонованого набору: 1, 2, 3, 4, 57

Розв’язання: всього 5 елементів, вибір дві цифри, порядок важливий, розміщення.

чисел

З 10 учнів необхідно вибрати двох для прибирання класу. Скількома способами можна це зробити?

Розв’язання: Всього 10 учнів, n = 10. Якщо вибирають двох для прибирання, то т = 2. Порядок неважливий, комбінація.

С = = = 45

Закріплення нового матеріалу.

Усне розв’язування задач

Скількома способами можна вибрати 4 яблука із 10? (Відповідь: С)
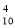Скількома способами можна розподілити 3 різні путівки до дитячих таборів між 20 учнями? (Відповідь: А)
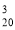Скількома способами можна розподілити три однакові путівки між 20 учнями? (Відповідь: С)
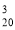Скількома способами можна сформувати поїзд з 8 вагонів? (Відповідь: Р₈)
У класі навчається 10 хлопців. Скількома способами можна їх вишикувати у шеренгу? (Відповідь: Р₁₀)
Скількома способами із 20 учнів можна обрати старосту класу та його замісника? (Відповідь: А)

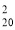Робота в парах.

Скількома способами можна розставити на полиці п’ять різних книжок? (Відповідь: Р₅)
З 10 учнів необхідно вибрати двох для прибирання класу. Скількома способами можна це зробити? (Відповідь: С)
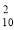У магазині є сім видів новорічних подарунків. Скількома способами можна вибрати з них три різні подарунки? (Відповідь: А)
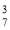Скількома способами можна сформувати поїзд із 10 вагонів? (Відповідь: Р₁₀)
На полиці 35 книжок. Скількома способами можна вибрати дві з них? (Відповідь: С)
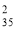Скількома способами можна розсадити 4 учнів на 25 місцях? (Відповідь: А)
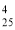Студенту треба скласти 4 екзамени протягом 8 днів. Скількома способами це можливо? (Відповідь: А)
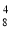Скількома способами можна скласти список із 9 прізвищ? (Відповідь: Р₉)
Перед чемпіонатом 12 капітанів команд потиснули один одному руки. Скільки рукостискань було зроблено? (Відповідь: С)

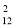Заповніть таблицю: Визначити вид сполук.

	Перестановка	Розміщення	Комбінація
Формула
№ задачі

ПІ учня: (відповідь)

	Перестановка	Розміщення	Комбінація
Формула	Р_п=п!
№ задачі	1. Р₅	3. А	2. С
	4. Р₁₀	6. А	5. С
	8. Р₉	7. А	9. С

Розв’язування задач.

Набір завдань.

1. Скількома способами можна дати клички чотирьом цуценятам, маючи набір з семи імен?

2. Скільки існує способів вибору з 13 осіб на п'ять вакантних посад?

3. З двох математиків і восьми економістів потрібно скласти комісію з восьми осіб. Скількома способами це можна зробити за умови, що в комісії повинен бути присутнім хоча б один математик?

4. Скількома способами можна розставити на полиці п'ять книг за умови , що певні дві з них повинні стояти поруч?

5. Набираючи номер телефону, абонент забув дві останні цифри . Скільки різних варіантів потрібно набрати, щоб дозвонитись, якщо він пам'ятає, що цифри різні і не нуль?

6 У шкільній олімпіаді з математики виявилося чотири переможця . Однак на районну олімпіаду можна відправити тільки двох. Скільки існує варіантів вибору цих двох учнів?

7. У одноколовому турнірі з футболу беруть участь 8 команд. Скільки існує варіантів призової трійки?

8. У фінальному забігу на 100 м беруть участь 8 спортсменів. Скільки існує варіантів протоколу пробігу?

9. У відбірковому турнірі за 3 путівки на чемпіонат світу беруть участь 10 команд. Скільки існує варіантів «щасливої трійки»?

10. На станції 7 запасних шляхів. Скількома способами можна розставити на них 4 потяги ?

Використання правила суми й добутку.

Комбінаторні задачі бувають різних видів. Але більшість із них розв’язуються за допомогою двох основних правил - правила суми та правила добутку.

ПРАВИЛО СУМИ (або а, або в)

Якщо елемент із множини А можна вибрати n способами, а з множини В - m способами, то вибір п або т можна здійснити (п + т) способами.

ПРАВИЛО ДОБУТКУ (і а, і в)

Якщо елемент із множини А можна вибрати т способами, а з множини В - п способами, то пару можна вибрати т · п способами.

Наприклад:

У класі 12 хлопців і 10 дівчат.

а) Скількома способами можна вибрати двох хлопців або трьох дівчат з групи?

Розв’язання: Порядок неважливий, вибір декількох елементів.

Хлопці: п = 12, вибір т = 2, С = = = 66 ,

Дівчата: п = 10, вибір т = 3 , С = = = 4 · 3 · 10 = 120

Вибір (або - або) за правилом суми: 66 + 120 = 186 способів.

б) Вибрати двох хлопців і трьох дівчат.

Розв’язання: Вибираємо пару: двох хлопців і трьох дівчат. За правилом добутку: 66 · 120 = 7920 способів.

Розв’язування задач:

Рота складається з 3 офіцерів, 6 сержантів і 60 рядових. Скількома способами можна виділити з них загін, що складається з офіцера, двох сержантів і п’яти рядових? Порядок неважливий.

Розв’язання: Одного офіцера вибираємо з С способами, сержантів С способами, а рядових Сспособами. Офіцер С = 3 способами.

Сержанти: С= = = 5 · 3 = 15. Рядові :С = = 97527 способами. Загін можна скласти 3 · 6 · 97527 = 1755486 способами.

Збори з 20 осіб обирають голову, секретаря та трьох членів редакційної комісії. Скількома способами це можна зробити?

Розв’язання: Вибір голови та секретаря - порядок важливий.

А = 20 · 19 = 380 способів обирати голову та секретаря.

З 18 осіб (20 - 2) вибираємо трьох членів редакційної комісії. Порядок вибору неважливий. С = = = 16 · 17 · 3 = 816 способів. Отже, для вибіру голови, секретаря і трьох членів комісії існує 380 ∙ 816=310080 способів.

Шаховий гурток відвідують дві дівчини та сім хлопців. Для участі у змаганнях необхідно скласти команду з чотирьох гравців, до якої обов’язково має входити хоча б одна дівчина. Скількома способами це можна зробити?

Розв’язання: «Хоча б одна» означає одна або дві дівчини.

1) У команду входить одна дівчина та три хлопця. Порядок неважливий.

С · С = 2 · = = 2 · 5 · 7 = 70

2) У команду входять дві дівчини та два хлопця. Порядок неважливий.

С · С = 1 · = = 3 · 7 = 21

3) За правилом суми: 70 + 21 = 91способів.

Навчальна самостійна робота:

Варіант 1

Скількома способами можна скласти список з 9 людей?
Скільки різних прямих можна провести через 5 точок площини, з яких ніякі три не лежать на одній прямій?
Скількома способами можна з 20 учнів призначити двох чергових, з яких один - старший?
З 10 різних троянд і 5 різних гербер потрібно скласти букет, що містить 3 троянди і 2 гербери. Скільки різних букетів можна скласти?

Варіант 2

Скількома способами можна з 20 учнів призначити двох чергових з однаковими обов’язками?
Скількома способами можна розставити на полиці 6 книг різних авторів?
Скількома способами із групи в 30 людей можна вибрати два делегата на конференцію, якщо делегати мають різні повноваження?
Збори з 30 людей обирають голову, секретаря, і трьох членів редакційної комісії. Скількома способами це можна зробити?

Варіант 3

25 учнів потиснули один одному руки. Скільки було зроблено рукостискань?
Скільки різних слів можна утворити з літер слова «школа»?
До складу профкому обрано 10 осіб. Серед них потрібно вибрати голову, його заступника і секретаря. Скількома способами це можна зробити?
Скількома способами можна групу із 15 учнів розділити на дві групи так, щоб в одній групі було 4учні, а в другій - одинадцять?

Варіант 4

Скількома способами можна вибрати 3 різні фарби з 5 різних фарб?
25 учнів обмінялися фотографіями так, що кожний обмінявся з кожним. Скільки було роздано фотографій?

Скількома способами можна розкласти 8 різних листів у 8 різних конвертів, якщо в кожний конверт вкладається лише один лист?
У взводі 5 сержантів і 30 солдат. Скількома способами можна скласти наряд із одного сержанта і трьох солдат?

V. Підсумки заняття

Слово викладача. Висновки про проведене заняття. Оцінювання учнів.

На прикладах розв’язаних задач ми побачили практичне застосування комбінаторики в різних сферах діяльності людини, з’ясували де в реальному житті ми зустрічаємося з комбінаторикою.

Області застосування комбінаторики:

навчальні заклади (складання розкладу)
сфера громадського харчування (складання меню)
спортивні змагання (розрахунки кількості ігор)
виробництво (розподіл кількох видів роботи)
азартні ігри (підрахунок частоти виграшу)
хімія ( аналіз можливих зв’язків між хімічними елементами)
економіка (аналіз варіантів купівлі - продажу)
доставка пошти ( варіанти пересилання)
біологія (розшифрування коду ДНК)
військова справа (розташування підрозділів)
астрономія (аналіз розташування планет та зірок)

VII. Домашнє завдання

Вивчити конспект. Розв’язати задачі.

У магазині є сім видів новорічних подарунків. Скількома способами можна вибрати з них три різні подарунки?
Скількома способами можна сформувати поїзд із 10 вагонів?
На полиці 35 книжок. Скількома способами можна вибрати дві з них?
Скількома способами можна розсадити 4 студентів на 25 місцях?
Студенту треба скласти 4 іспити протягом 8 днів. Скількома способами це можливо?

VIII. Рефлексія

На занятті був Активний/ пасивний

Своєю роботою на занятті Задоволений/ незадоволений

Урок для мене видався Захоплюючим/нудним

На уроці втома Не відчувалася/відчувалась

Мій настрій Став краще/став гірше

Матеріал уроку мені був Зрозумілим/не зрозумілим

Цікавий/не цікавий

Домашнє завдання мені здається Легким/складним

Середня оцінка розробки

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

Загальна:

5.0

Всього відгуків: 1

Оцінки та відгуки

Чернюк Наталія 24.09.2023 в 20:11

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

docx

Завантажити

Зберегти на потім

Додав(-ла)

Безотосна Анна Павлівна

Пов’язані теми

Алгебра, 11 клас, Розробки уроків

Додано

24 лютого 2023

Переглядів

3731

Оцінка розробки

5.0 (1 відгук)