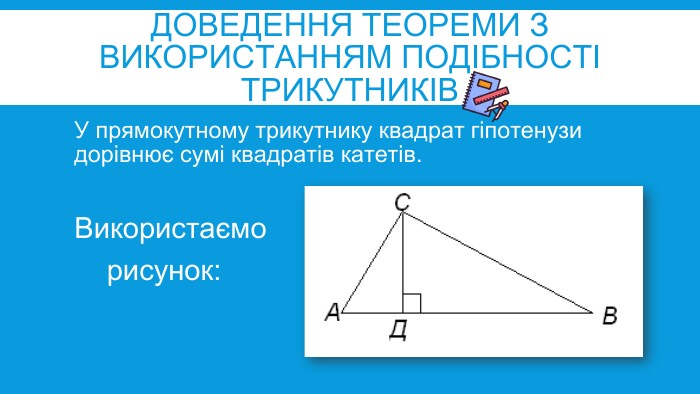
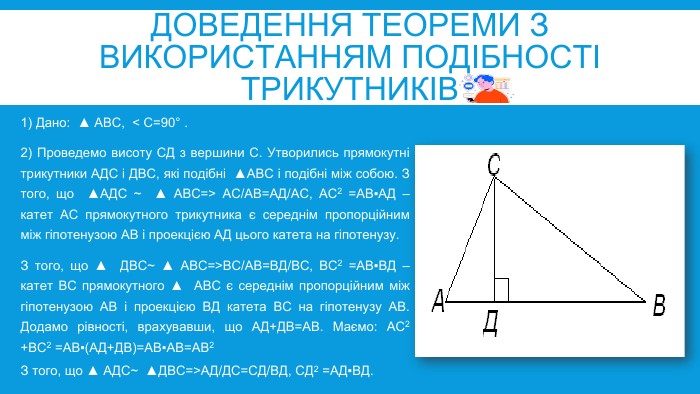
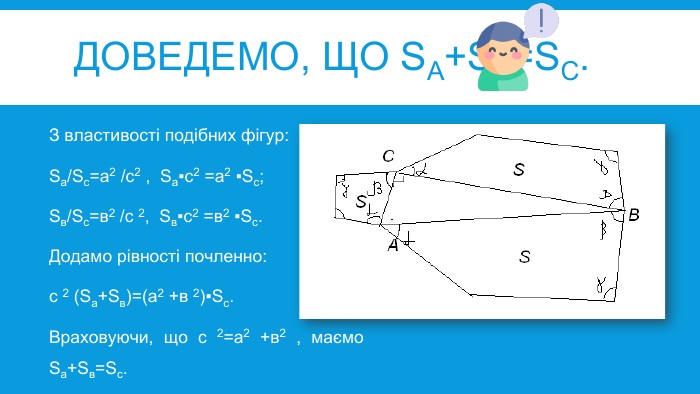
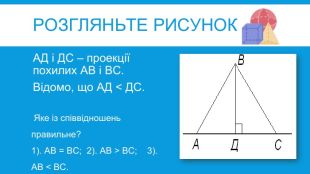
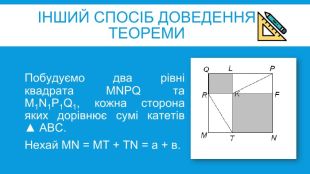
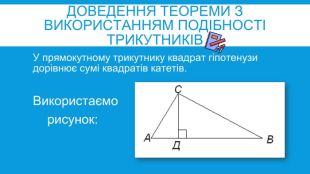
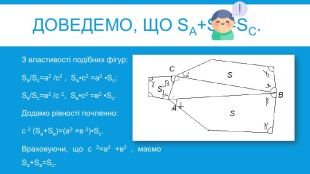
УРОК ДОСЛІДЖЕННЯТЕМА: ТЕОРЕМА ПІФАГОРА. РІЗНІ ДОВЕДЕННЯ ТЕОРЕМИ ПІФАГОРА
Про матеріал
УРОК ДОСЛІДЖЕННЯ ТЕМА: ТЕОРЕМА ПІФАГОРА. РІЗНІ ДОВЕДЕННЯ ТЕОРЕМИ ПІФАГОРА Автор: Плейзор Катерина Тимофіївна
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку