"Презентація на тему: Показникова функція, її графік та властивості"
Показникова функція, її графік та властивості.
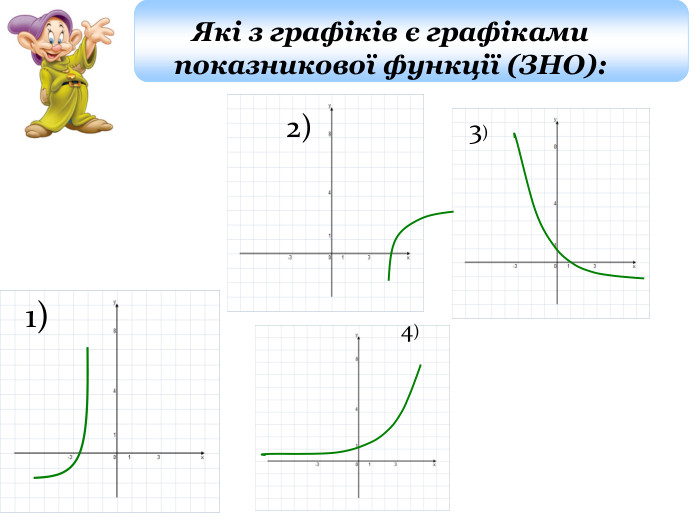
Навчальна: засвоїти означення показникової функції, властивості показникової функції, навчитися будувати графіки показникової функції; навчитись використовувати властивості показникової функції при розв’язуванні вправ та робити висновки; Розвиваюча: розвивати вміння аналізувати графіки показникової функції та, користуючись побудованими графіками, аналізувати властивості показникової функції; Виховна: виховувати інтерес до вивчення точних наук, показати, де саме застосовують у житті властивості показникової функції;виховувати культуру мови.
Дайте означення функції. Числова функція – залежність між двома числовими змінними, якщо кожному числу х відповідає єдине число у Математика – це сила!!!
Що називають областю визначення функції? Математика – це розум!!! Область визначення функції – це множина значень, яких може набувати аргумент х – позначається D(y), або область допустимих значень функції (ОДЗ)
Що називають областю значення функції? Будь – яка галузь виробництва без математики безсила!!! Область значень функції – це множина значень, яких може набувати залежна змінна у за всіх значень х – позначається Е(y)
Ви тільки подивіться на ефективність наших, українських дронів.
Математика – це сила!!! Математика – це розум!!! Будь- яка галузь виробництва без математики безсила!!! Ви тільки подивіться на ефективність наших, українських дронів. Процвітання та інтереси держави тісно пов’язані з математикою і добробутом. Наполеон
Показникова функція, її графік та властивості.
“ Деякі види трансцендентних функцій, які часто зустрічаються, перш за все показникові, відкривають доступ до багатьох досліджень.” Леонард Ейлер
Вивчення нового матеріалу Функцію, яку задано формулою у = ах (де а>0, а ≠ 1), називають показниковою функцією. ( з основою а) y = πx
Оберіть із заданих функцій показникові : Функція y=ax , де a>0 і a≠1
x -3 -2 -1 0 1 2 3 y=2x 1 2 4 8 Властивості: 1) D(y)=R ; 2) E(y)=(0;∞); 3) Функція зростає при xєR ; 4) Графік функції перетинає Oy в точці (0;1). Графік показникової функції:
x -3 -2 -1 0 1 2 3 8 4 2 1 Графік показникової функції 3) Функція спадає при xєR ; 4) Графік функції перетинає Oy в точці (0;1). Властивості: 1) D(y)=R ; 2) E(y)=(0;∞);
Загальні властивості y=ax,(a>0,a≠1) Графік показникової функції називається експонентою.
Які з графіків є графіками показникової функції (ЗНО): 1) 2) 3) 4)
Серед наведених функцій вибрати ті, що спадають.
Серед наведених функцій вибрати ті, що зростають.
Порівняти значення виразів: ( а= 5>1, то функція зростає); Застосування властивостей
(із збільшенням показника степінь збільшується, тому a > 1). Порівняти x і y, якщо: (0<0,3<1, то x
Порівняйте числа x і y, якщо: а = 1,5, а > 1, то x < y а = 0,3, а < 1, то x < y Застосування властивостей
“ Деякі види трансцендентних функцій, які часто зустрічаються, перш за все показникові, відкривають доступ до багатьох досліджень.” Леонард Ейлер Підсумки уроку
Радіоактивний розпад М = М0(1/2)t/T Коли радіоактивна речовина розпадається, її кількість зменшується. Через деякий час залишиться половина початкової кількості речовини. Цей проміжок часу Т називається періодом напіврозпаду речовини. Через t років маса М речовини буде дорівнювати де М 0 – початкова маса речовини. Чим більший період напіврозпаду, тим повільніше розпадається речовина. Явище радіоактивного розпаду використовується для визначення віку археологічних знахідок, наприклад, визначено приблизний вік Землі, біля 5,5 млрд років, для підтримки еталону часу.
Приріст капіталу в банку де А — шукана величина, А0, — початковий вклад, Р — річний відсоток, t — розрахунковий термін. Приріст капіталу в банку здійснюється за законом природного зростання. Всім відома формула складних відсотків: А = А0(1+р/100)t
Ріст населення де N0 – кількість людей при t = 0, N – кількість людей в момент часу t, а, e – постійні величини. Зміна кількості людей в країні за великий проміжок часу t описується формулою: N = N0eat
Приріст деревини Дерево росте так, що кількість деревини в початковий момент збільшується з часом за законом: m=m 0 a k t де m 0 – кількість деревини в початковий момент, k – деяка постійна, t – час у роках.
Барометрична формула При постійній температурі атмосферний тиск змінюється залежно від висоти над рівнем моря за законом: Р=Р0 а h де Р0 – атмосферний тиск над рівнем моря, Р – тиск на висоті h, а – деяка постійна (залежить від температури).
Коливання маятника Оскільки множник e-kt зменшується з плином часу, то розмах коливань стає все меншим і меншим Якщо при коливаннях маятника не нехтувати опором повітря, то амплітуда коливань стає все меншою, коливання затухають. Відхилення точки, що здійснює затухаючі коливання, виражається формулою: S = Ae-kt sin(ωt + φ0)
Розмноження бактерій де a >1 – постійна величина, що характеризує швидкість росту даної колонії і залежить від біологічного виду організмів та умов зовнішнього середовища. Колонія живих організмів (зокрема, бактерії) зростає в результаті розмноження. Якщо за рівні проміжки часу число живих організмів збільшується в одне й те саме число разів, то число N організмів по закінченні часу t після початку спостережень виражається формулою N=na t
Вивчити теорію; Виконати вправи: Не махай на все рукою, не лінуйся, а учись, Бо, чого навчишся в нас ти , знадобиться ще колись! Домашнє завдання:
про публікацію авторської розробки
Додати розробку