Презентація на тему:“Розв’язування задач за допомогою теореми Піфагора”.
Про матеріал
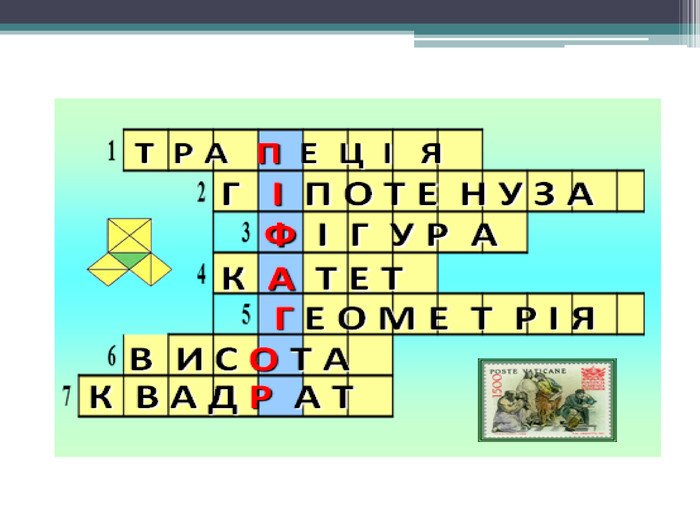
Геометрія володіє двома скарбами :один із них – це теорема Піфагора.
Йоганн Кеплер.
В презентації розглянуто кілька способів доведення теореми Піфагора.Написана десь між 500 до н. е. і 200 до н. е.китайська математична книга «Чу Пей» (周髀算经)дає візуальне доведення теореми Піфагора,яка в Китаї називається теорема Гугу (勾股定理),для трикутника із сторонами (3, 4, 5). Індійський математик Бхаскара у своїй праці «Вінок систем» наводить приклад доведення теореми Піфагора у вигляді креслення з підписом «Дивись!».
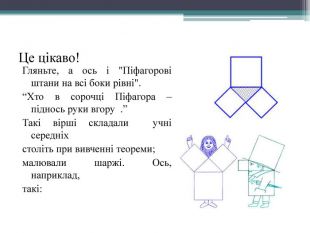
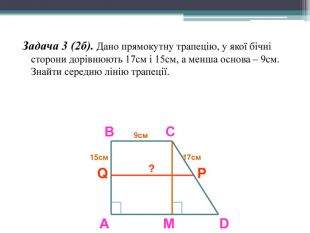
Презентація містить слайди з старовинними задачами,які розв'язуються за допомогою теореми Піфагора.
Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку