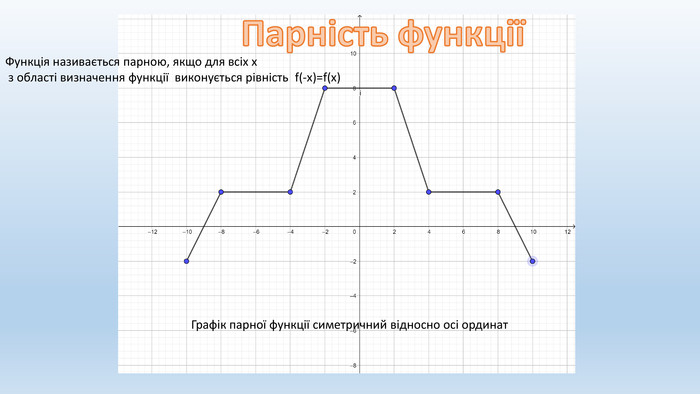
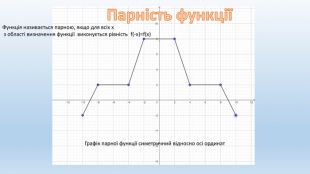
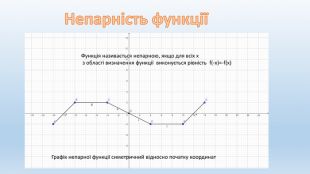
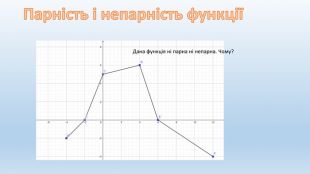
Презентація на тему "Властивості функцій"
Про матеріал
В даній презентації описуються властивості функції, в загальному вигляді. Може бути корисним при вивченні властивостей функцій в 9, 10, 11 класах Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


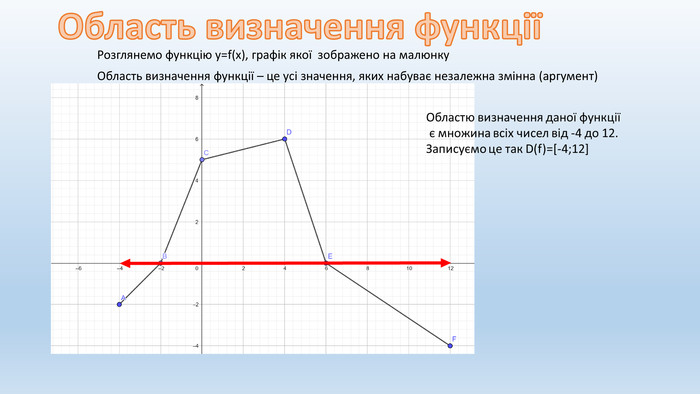
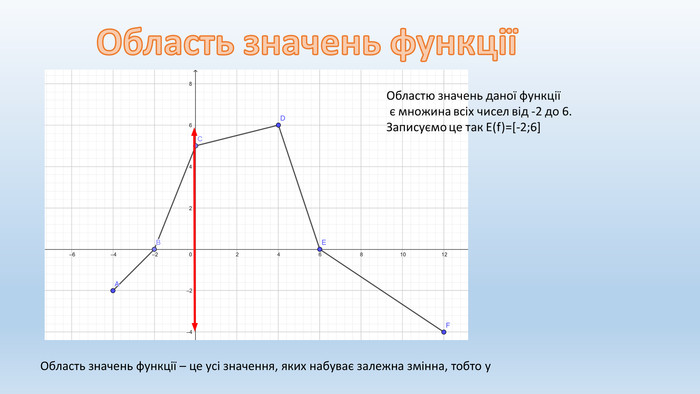
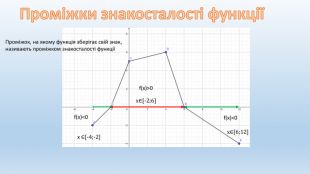
![Проміжок, на якому функція зберігає свій знак, називають проміжком знакосталості функціїf(x)<0f(x)>0x∈[-2;6]x ∈[-4;-2]x∈[6;12]Проміжки знакосталості функції Проміжок, на якому функція зберігає свій знак, називають проміжком знакосталості функціїf(x)<0f(x)>0x∈[-2;6]x ∈[-4;-2]x∈[6;12]Проміжки знакосталості функції](/uploads/files/181722/201058/217067_images/6.jpg)
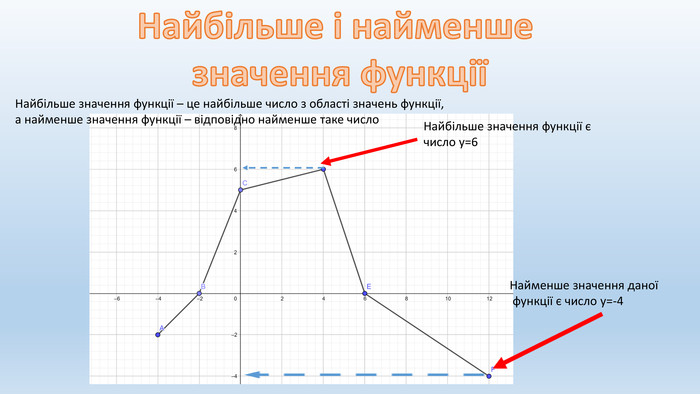
![Функцію називають зростаючою на деякому проміжку, якщо на цьому проміжкубільшому значенню аргументу, відповідає більше значення функції. Тобто, якщо із збільшенням х, у «прямує вгору»Дана функція зростає на проміжкух ∈ [-4;4]зростаєЗростання функції Функцію називають зростаючою на деякому проміжку, якщо на цьому проміжкубільшому значенню аргументу, відповідає більше значення функції. Тобто, якщо із збільшенням х, у «прямує вгору»Дана функція зростає на проміжкух ∈ [-4;4]зростаєЗростання функції](/uploads/files/181722/201058/217067_images/7.jpg)
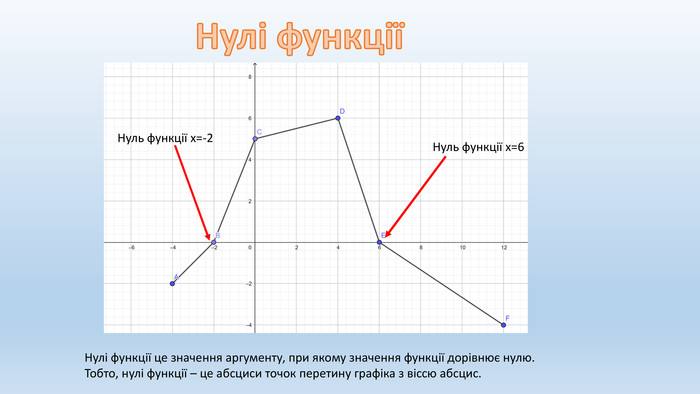
![Функцію називають спадною на деякому проміжку, якщо на цьому проміжкубільшому значенню аргументу, відповідає менше значення функції. Тобто, якщо із збільшенням х, у «прямує вниз»Дана функція спадає на проміжкух ∈ [4;12]спадаєСпадання функції Функцію називають спадною на деякому проміжку, якщо на цьому проміжкубільшому значенню аргументу, відповідає менше значення функції. Тобто, якщо із збільшенням х, у «прямує вниз»Дана функція спадає на проміжкух ∈ [4;12]спадаєСпадання функції](/uploads/files/181722/201058/217067_images/8.jpg)