Інтеграл

План

1. Вступ

-       Визначення нтеграла

-       Історичний контекст

-       Значення нтеграла в математиц

2. Інтеграл в алгебр

-       Поняття перв сної функц ї

-       Невизначений нтеграл

-       Властивост невизначеного нтеграла

-       Методи обчислення невизначеного нтеграла

3. Інтеграл в геометр ї

-       Визначений нтеграл як м ра площ

-       Властивост визначеного нтеграла

-       Геометричний зм ст теореми про середнє значення нтеграла

-       Застосування визначеного нтеграла в геометр ї

4. Застосування нтеграл в

-       Практичн приклади обчислення нтеграл в

5. Висновки

-       Значення вивчення нтеграл в для розвитку математичних навичок

Вступ

Визначення інтеграла

Інтеграл — узагальнення поняття суми неск нченного числа неск нченно малих доданк в.

Історичний контекст

Застосування інтеграла в математиці

Одне з найважливших понять математичного аналзу, центральне поняття нтегрального числення, застосовується для розв'язання задач:

                                                          2        3                    4

обчислення пройденогоза нер вном рногоруху шляху неоднор дногомасит ла в дновлення⁽невизначенийза її пох дною функц ї площ п д

кривою

нтеграл)

Інтеграл в алгебрі

Поняття первісної функції

Перв сна функц я – особлива функц я, пох дна якої дор внює дан й функц ї. Іншими словами, перв сна функц я є функц єю, яка в дновлюється при її диференц юванн .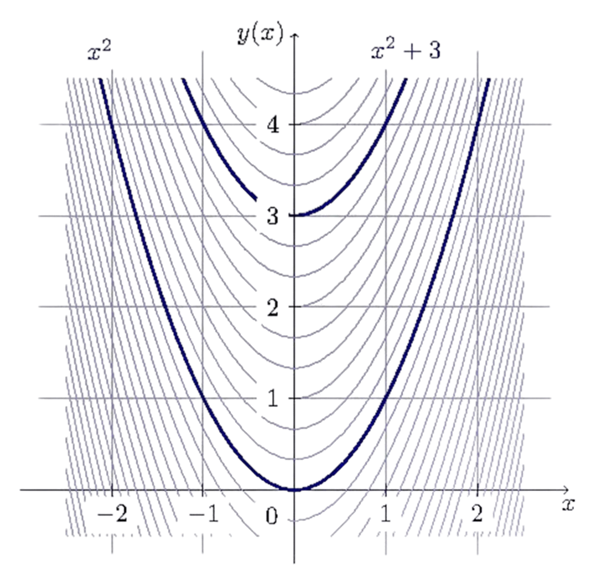

Невизначений інтеграл

Неви́значений нтегра́л для функц ї f — це сукупн сть ус х перв сних ц єї функц ї. Завдання диференц ального числення — обчислення пох дної в д заданої функц ї y = f(x).

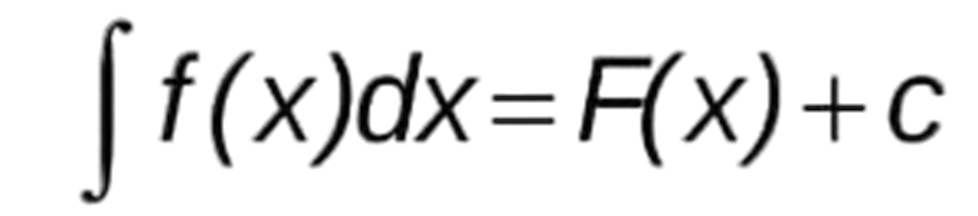
Властивості невизначеного

інтеграла

1.            (∫f(x)dx)'=f(x)

2.            ∫F'(x)dx=F(x)+C

3.            ∫kf(x)dx=k∫f(x)dx, якщо k≠0.

4.            ∫(f(x)±g(x))dx=∫f(x)dx±∫g(x)dx

Методи обчислення невизначеного інтеграла

Для обчислення невизначених нтеграл в використовуються

 Таблиця основних формул нтегрування;  Метод п дстановки (або формула зам ни зм нної);  Метод нтегрування частинами.

За допомогою згаданих метод в можна обчислювати невизначен нтеграли у вигляд ск нченних комб нац й елементарних функц й. Проте, не вс нтеграли можна виразити через елементарн функц ї. В домо небагато клас в функц й, нтегрування яких, у п дсумку дає елементарн функц ї. До цих клас в в дносяться рац ональн , тригонометричн , показников функц ї та функц ї з радикалами.

Інтеграл в геометрії

Визначений інтеграл як міра площі

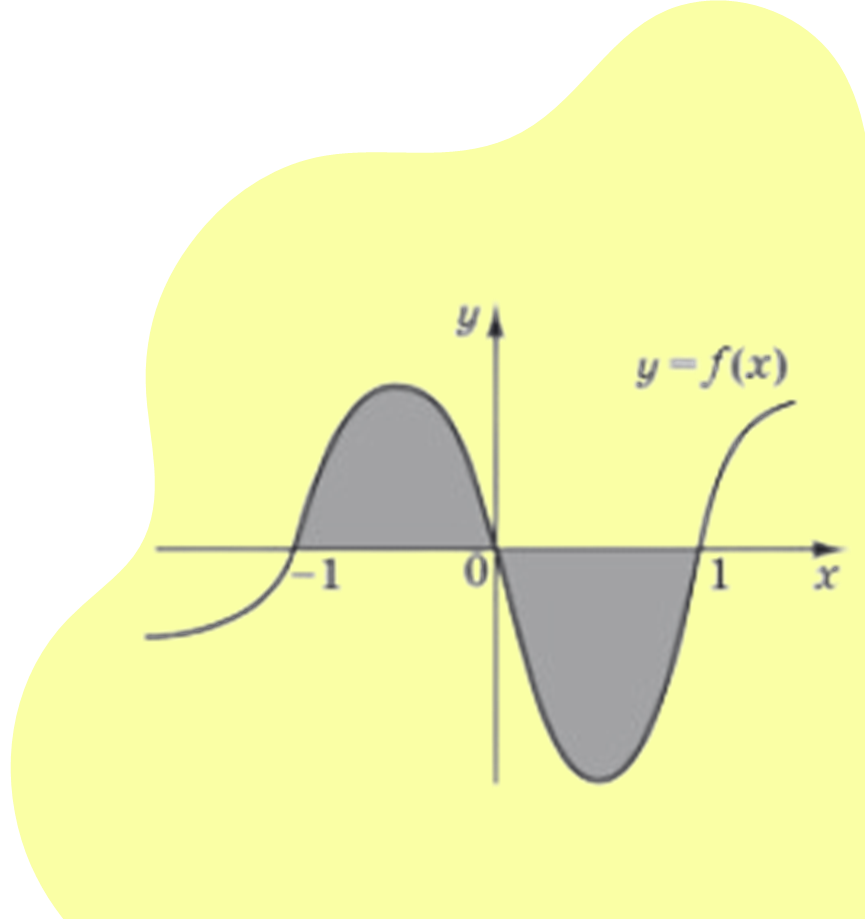Визначений нтеграл використовується в математиц для обчислення площ ф гур, обмежених граф ками функц й. Це широко застосовується в геометр ї, зокрема для знаходження площ ф гур, обмежених граф ками функц й, та об’єм в т л.

Основні

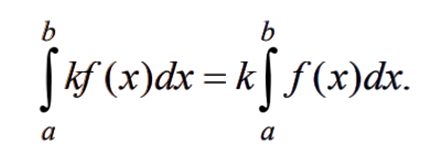властивості  Сталий множник можна визначеного  виносити за знак _{інтеграла}  визначеного нтеграла, тобто

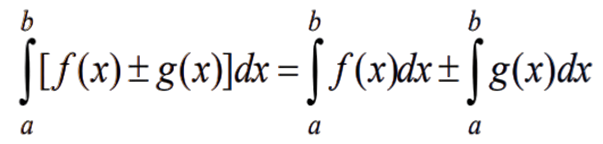Визначений нтеграл в д алгебраїчної  суми функц й дор внює алгебраїчн й сум їх нтеграл в, тобто

Як б не були числа має м сце р вн сть

Якщо всюди на в др зку [a,b], де a<b функц я f(x)>0, то Якщо всюди на в др зку [a,b], f(x)<g(x), (a>b), то

Для функц ї f(x), визначеної на

 в др зку [a,b], (a,b) має м сце нер вн сть

Якщо M  m – в дпов дно найменше  найб льше значення функц ї f(x) на в др зку [a,b], то

Теорема 3 (теорема про середнє): Якщо функц я f(x) неперервна на в др зку [a,b] , то на цьому в др зку снує точка така C, що

Геометричний зміст теореми про середнє значення інтеграла

Геометричний зм ст теореми про середнє значення визначеного нтеграла полягає в тому, що снує прямокутник з сторонами (b - a), який р вновеликий кривол н йн й трапец ї (aАВв) за умови, що функц я (f(x)) неперервна на пром жку ([a; b]). Це можна уявити так: якщо ми побудуємо прямокутник з висотою (f(c)), де (c) - це деяке число з пром жку ([a; b]), то площа цього прямокутника буде р вна площ п д граф ком функц ї (f(x)) на цьому пром жку.

Таким чином, теорема про середнє значення визначеного нтеграла вказує на снування такої точки (c), де f(с) дор внює середньому значенню функц ї (f(x)) на пром жку ([a; b]). Ця теорема має важлив застосування в математичному анал з та ф зиц

Застосування визначеного інтеграла в геометрії

Застосування визначеного нтеграла в геометр ї має дек лька ц кавих аспект в.

Давайте розглянемо деяк з них:

Обчислення площ Обчислення об’єму плоских ф гур т л обертання

Використовуючи поняття визначеного нтеграла, можна обчислювати площ       Визначений нтеграл також плоских ф гур.Наприклад, площа     допомагає обчислювати об’єми

кривол н йної трапец ї, обмеженої    т л обертання навколо осей

граф ком нев д’ємної, неперервної        координат. Наприклад, якщо

функц ї, в др зком ос Ох та в др зками     ми маємо криву, яка

прямих, обчислюється за в дпов дною обертається навколо ос Ох, ми формулою. Це дозволяє нам можемо визначити об’єм цього

Обчислення довжини дуги плоскої кривої

Визначений нтеграл також дозволяє визначити довжину дуги плоскої кривої. Це

корисно, наприклад, при вивченн траєктор й руху об’єкт в.

визначити площу р зних       т ла за допомогою в дпов дної геометричних ф гур.    формули.

Застосування інтегралів

Практичні приклади обчислення інтегралів

Обчислення нтеграл в за допомогою лишк в: В део на YouTube розглядає приклади, в яких з

використанням вичет в обчислюються нтеграли в д

функц й комплексної зм нної по замкнутому контуру,

деяк нтеграли Р мана та несобственн нтеграли в д функц й д йсної зм нної1. Заняття ведеться українською мовою.

Застосування визначеного нтеграла: Інтеграл може бути використаний для обчислення площ плоских

ф гур у систем декартових та полярних координат, а також для знаходження роботи зм нної сили.

Висновки

Значення вивчення інтегралів для розвитку математичних навичок

Розум ння поняття площ та об’єму: Інтеграл допомагає нам обчислювати площу п д кривими л н ями, об’єм т л та нш геометричн характеристики. Наприклад, визначений нтеграл може вказати площу п д граф ком функц ї. Застосування в ф зиц та нженер ї: Інтеграл використовується для обчислення роботи, маси, центру мас, моменту нерц ї та багатьох нших параметр в. Наприклад, визначений нтеграл може допомогти обчислити роботу, яку виконує сила при перем щенн об’єкту.

Математична анал з та диференц альн р вняння: Інтеграл є важливою частиною математичного анал зу. В н допомагає розв’язувати диференц альн р вняння, знаходити функц ї розпод лу ймов рност та багато ншого.

 П дготовка до вищих математичних курс в: Вивчення нтеграл в є передумовою для б льш глибокого розум ння математики. Вони

використовуються в курсах анал зу, векторного анал зу, теор ї поля та нших спец ал зованих дисципл нах.

Джерела

ВИЗНАЧЕНИЙ ІНТЕГРАЛ. ОБЧИСЛЕННЯ ПЛОЩ І ОБ’ЄМІВ.

Первісна функція: Поняття, властивості та застосування

Основні властивості невизначеного інтеграла

III. Функції. Частина 8. Первісна та визначений інтеграл. Застосування визначеного інтеграла до обчислення площ плоских фігур

Обчислення визначених інтегралів. Застосування визначеного інтегралу

Лекція 14. Визначений інтеграл та його властивості.

Застосування визначеного інтеграла в геометрії Визначений інтеграл, його властивості, обчислення і застосування

Розділ ііі Застосування визначеного інтеграла до задач геометрії та розв’язку задач з фізики та механіки