Визначений інтеграл, його властивості, обчислення і застосування

Дистанційне навчання

 

Дисципліна «ВИЩА МАТЕМАТИКА»

 

ЛЕКЦІЯ

 

Тема: Визначений інтеграл, його властивості, обчислення і застосування.

Мета: ознайомитись з поняттям визначеного інтеграла, його властивостями, геометричним, фізичним та економічним змістом; дізнатись як обчислюються визначені інтеграли за формулою Ньютона-Лейбніца, методом заміни змінної, інтегруванням частинами; з’ясувати яким чином за допомогою визначеного інтеграла знаходять площі плоских фігур, довжину дуги кривої, об’єм тіла обертання.

 

План

1. Поняття визначеного інтеграла.
2. Геометричний, фізичний та економічний зміст визначеного інтеграла.
3. Властивості визначеного інтеграла.
4. Визначений інтеграл як функція верхньої межі. Формула Ньютона-Лейбніца.
5. Методи обчислення визначеного інтеграла: метод заміни змінної, інтегрування частинами.
6. Застосування визначеного інтеграла до обчислення площ плоских фігур.
7. Застосування визначеного інтеграла до знаходження довжини дуги кривої.
8. Застосування визначеного інтеграла до обчислення об’єму тіла обертання.

 

Рекомендована література

1. Берегова Г. І. Математика для економістів: вища математика (друга частина): навч. посібник / Г. І. Берегова, В. Н. Гладунський. – К. : УБС НБУ, 2014. – 279 с.     

URL: http://dspace.ubs.edu.ua/jspui/bitstream/123456789/598/1/Beregova_Mathematical_econom%282%29_9.pdf

2. Мацкул В.М. Вища математика для економістів.: Підручник.- Одеса: ОНЕУ, 2018.- 472с.

URL:

http://dspace.oneu.edu.ua/jspui/bitstream/123456789/7943/1/%D0%92%D0%B8%D1%89%D0%B0%20%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0%20%D0%B4%D0%BB%D1%8F%20%D0%B5%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D1%96%D1%81%D1%82%D1%96%D0%B2.pdf

ХІД ЗАНЯТТЯ

І.ОПАНУЙТЕ ТЕОРЕТИЧНИЙ МАТЕРІАЛ, ЗВЕРТАЮЧИ ОСОБЛИВУ УВАГУ НА РОЗВ’ЯЗАННЯ ПРИКЛАДІВ.

1. Поняття визначеного інтеграла

Нехай — деяка функція, що задана на проміжку [a; b]. Розіб’ємо [a; b] на n частин точками так що

Обчислимо де

Складемо інтегральну суму .

Позначимо .

Означення. Якщо існує скінченна границя інтегральних сум S_n при і не залежить ні від способу розбиття [a; b] на частини , ні від вибору точок , то ця границя називається визначеним інтегралом від функції на проміжку [a; b] і позначається:

, 

де        — знак визначеного інтеграла;

а, b  — нижня та верхня межі інтегрування;

f(x)  — підінтегральна функція;

f(x) dx      — підінтегральний вираз;

dx  — диференціал змінної інтегрування.

За означенням, визначений інтеграл — число, яке залежить від типу функції та проміжку [a; b]; він не залежить від того, якою буквою позначена змінна інтегрування:

Означення. Функція, для якої на [a; b] існує визначений інтеграл називається інтегровною на цьому проміжку.

Зауваження: неперервні функції — інтегровні.

2. Геометричний, фізичний та економічний зміст визначеного інтеграла

 

2.1.Геометричний зміст визначеного інтеграла

 

Задача про криволінійну трапецію

 

 

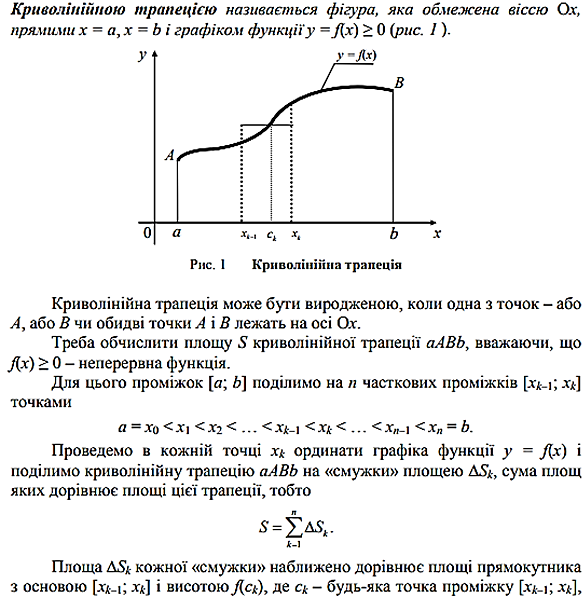
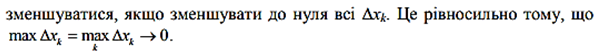
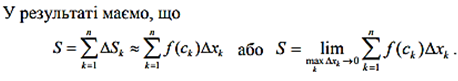
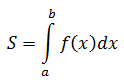
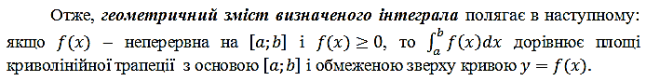
2.2.Фізичний зміст визначеного інтеграла

 

2.3.Економічний зміст визначеного інтеграла

 

 

 

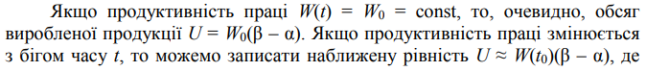
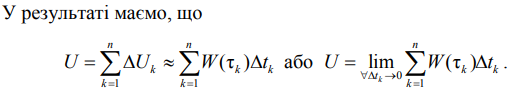
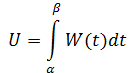
3. Властивості визначеного інтеграла

І. Якщо , то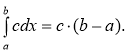

ІІ. Сталий множник можна виносити за знак визначеного інтеграла, тобто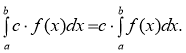

ІІІ. Визначений інтеграл від алгебраїчної суми двох функцій дорівнює такій же алгебраїчній сумі визначених інтегралів від цих функцій, тобто:

Ця властивість поширюється на будь-яке скінченне число доданків.

IV. Якщо у визначеному інтегралі поміняти місцями межі інтегрування, то інтеграл змінить лише свій знак на протилежний, тобто

V. Визначений інтеграл з однаковими межами інтегрування дорівнює нулю

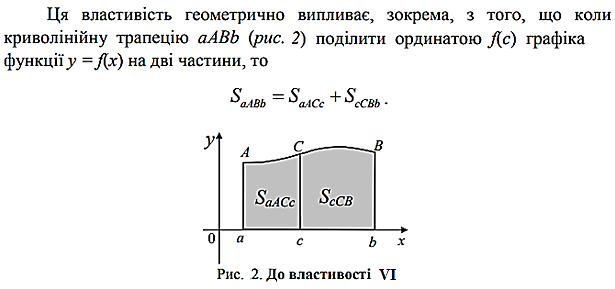
VI. Якщо точка с ділить проміжок [a; b] на частини [a;с] і [с;b], то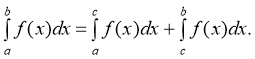

VII. Якщо і інтегровна для то

VIII. Якщо , — інтегровні та для то

IX. Якщо f(x) — інтегровна та для то

Х. Теорема  (про середнє).

Якщо функція — неперервна для то знайдеться така точка що:

 

Геометричний зміст теореми про середнє полягає в тому, що існує прямокутник із сторонами та b – a, який рівновеликий криволінійній трапеції аАВв за умови, що функція та неперервна на проміжку [a; b] (рис. 3).

              Рис. 3

 

 

4. Визначений інтеграл як функція верхньої межі. Формула Ньютона-Лейбніца

Розглянемо інтеграл , який буде функцією від верхньої межі інтегрування. Змінній х надамо приросту , що зумовить приріст функції.

   (рис. 4)

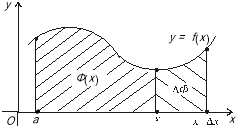
               Рис. 4

 

Теорема. Якщо функція f(x) неперервна для будь-якого то похідна від інтеграла зі змінною верхньою межею інтегрування по цій межі дорівнює підінтегральній функції від верхньої межі інтегрування, тобто

     

Наслідки:

1. Визначений інтеграл зі змінною верхньою межею від функції є одна із первісних для .

2. Будь-яка неперервна функція на проміжку має на цьому проміжку первісну, яку, наприклад, завжди можна побудувати у вигляді визначеного інтеграла зі змінною верхньою межею, тобто

Приклад. Знайти .

 Функція — неперервна на проміжку тому

Теорема. (Ньютона—Лейбніца). Якщо функція — неперервна для то визначений інтеграл від функції на проміжку дорівнює приросту первісної функції на цьому проміжку, тобто

  де  

Позначимо дію подвійної підстановки так: 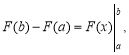тоді зв’язок між визначеним та невизначеним інтегралами можна подати такою рівністю:

  

Наслідок. Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральних функцій і виконати над нею подвійну підстановку.

Приклад.

 

 

5. Методи обчислення визначених інтегралів: заміна змінної, інтегрування частинами

 

5.1.Заміна змінних у визначеному інтегралі

 

НАВЧАЛЬНЕ  ВІДЕО: https://www.youtube.com/watch?v=zHk4jmOd58A

 

КОНСПЕКТ:

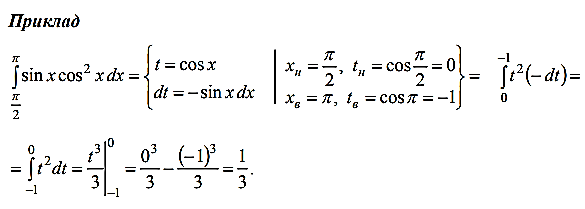
5.2.Інтегрування частинами визначеного інтеграла

 

НАВЧАЛЬНЕ  ВІДЕО: https://www.youtube.com/watch?v=wosbPOXZIQw

 

КОНСПЕКТ:

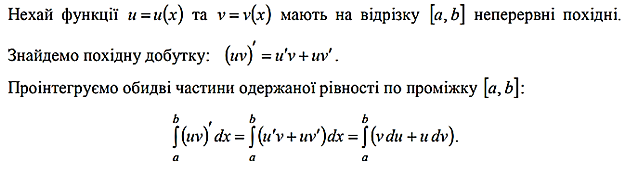
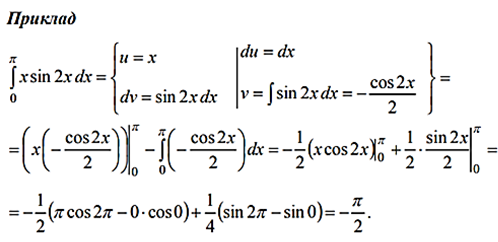
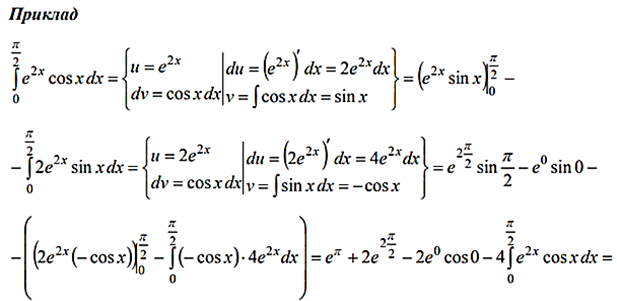
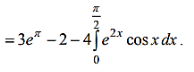
6.Застосування визначеного інтеграла до обчислення площ плоских фігур

НАВЧАЛЬНЕ  ВІДЕО: Обчислення площі інтегралом  https://www.youtube.com/watch?v=M81tYy7GqVQ&list=RDCMUCVZa4xxoM20mRqZKiy2cUiA&index=2

 

7. Застосування визначеного інтеграла до знаходження довжини дуги кривої.

НАВЧАЛЬНЕ  ВІДЕО: Довжина дуги кривої

https://www.youtube.com/watch?v=AMpxWhPSdv4

 

8. Застосування визначеного інтеграла до обчислення об’єму тіла обертання.

НАВЧАЛЬНЕ  ВІДЕО: Об'єм тіла обертання

https://www.youtube.com/watch?v=cHDxUENXeMc

 

 

 

 

ІІ. ДЛЯ ПОВТОРЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ ПЕРЕГЛЯНЬТЕ ПРЕЗЕНТАЦІЮ: «ВИЗНАЧЕНИЙ ІНТЕГРАЛ, ЙОГО ВЛАСТИВОСТІ, ОБЧИСЛЕННЯ І ЗАСТОСУВАННЯ» (див. https://naurok.com.ua/biblioteka матеріали Костюкович В.В.)