Презентація :Паралельне перенесення,симетрія.
Про матеріал
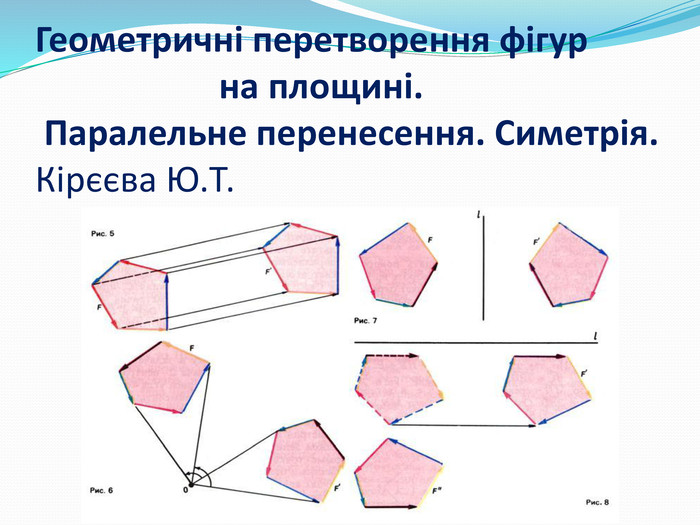
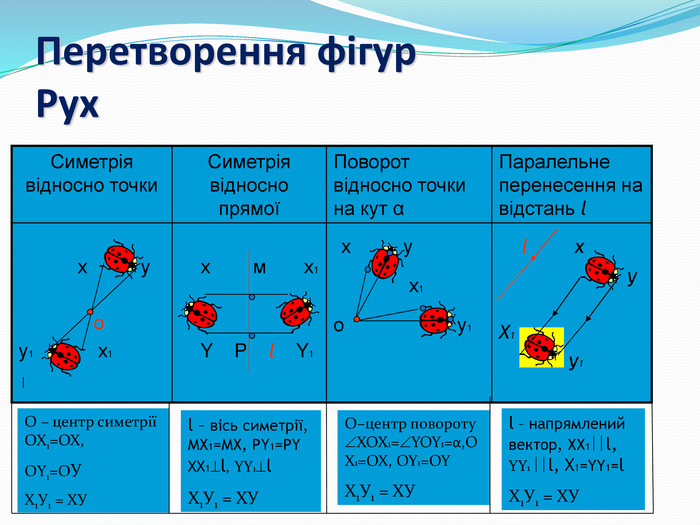
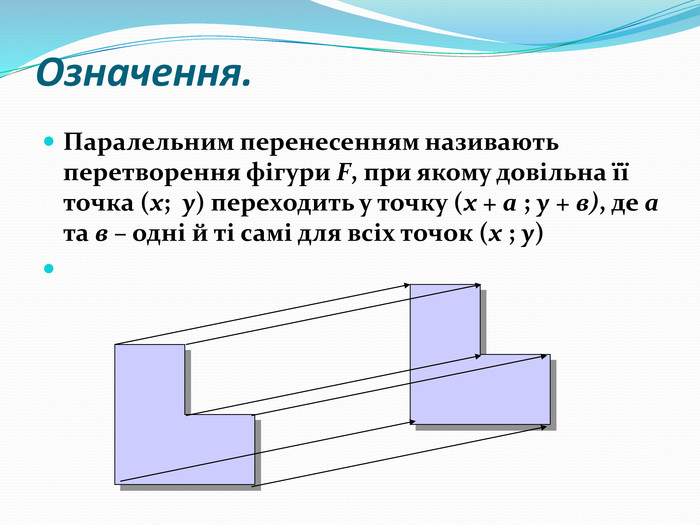
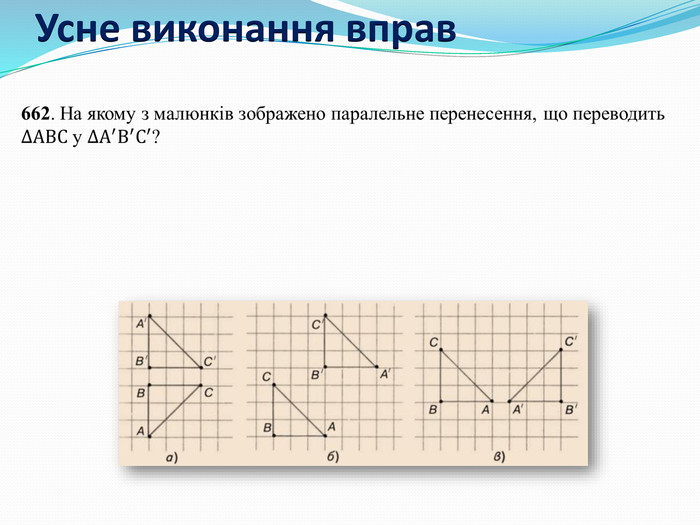
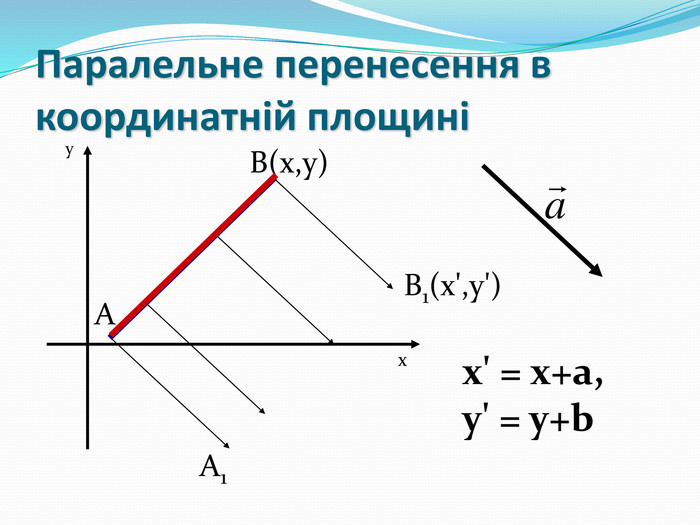
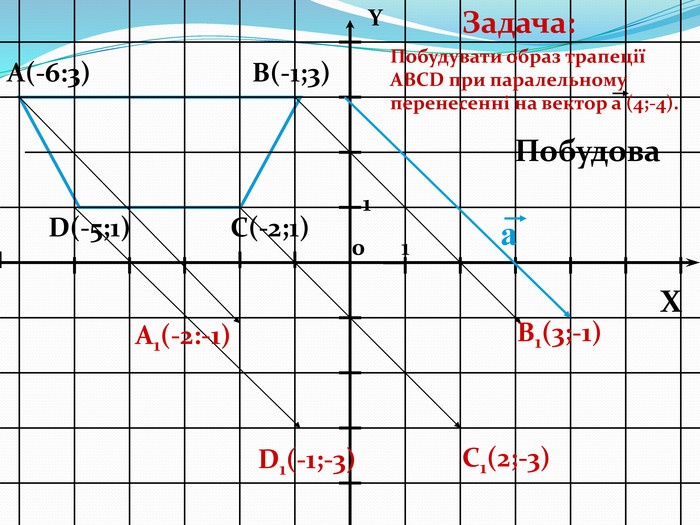
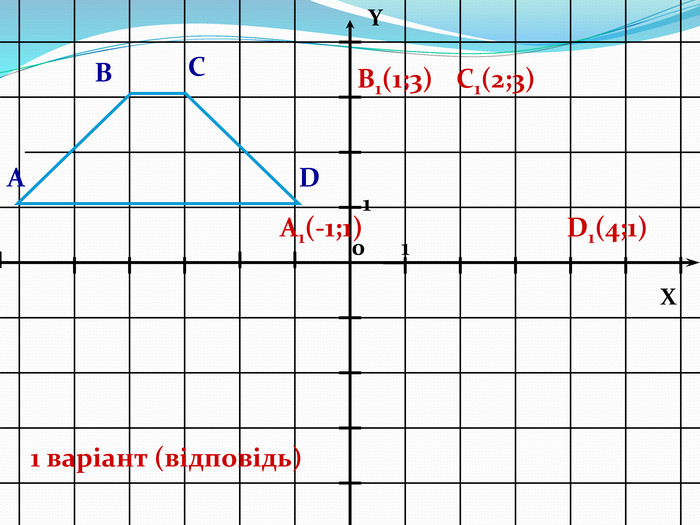
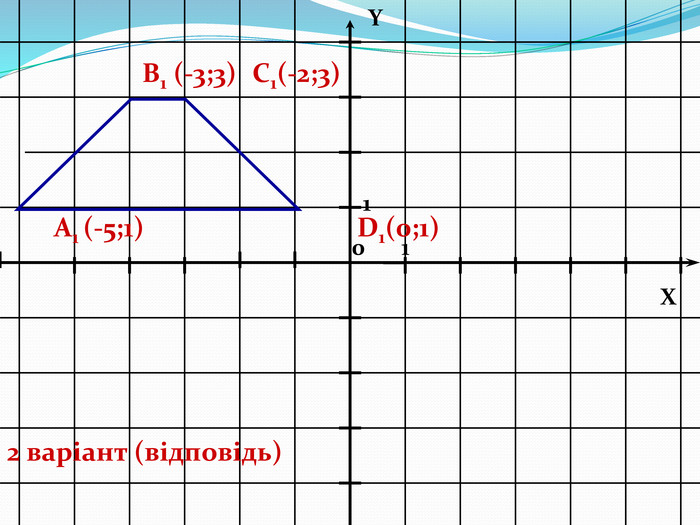
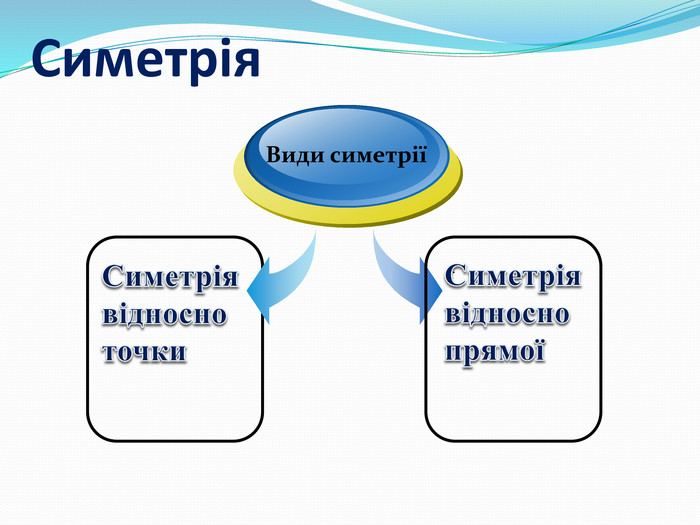
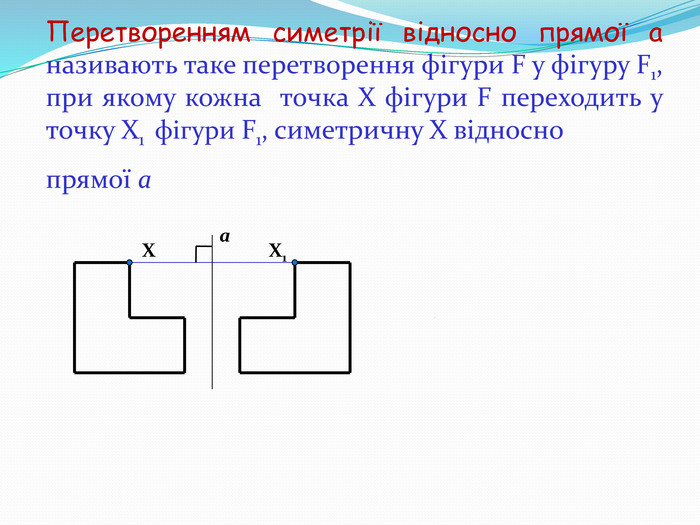
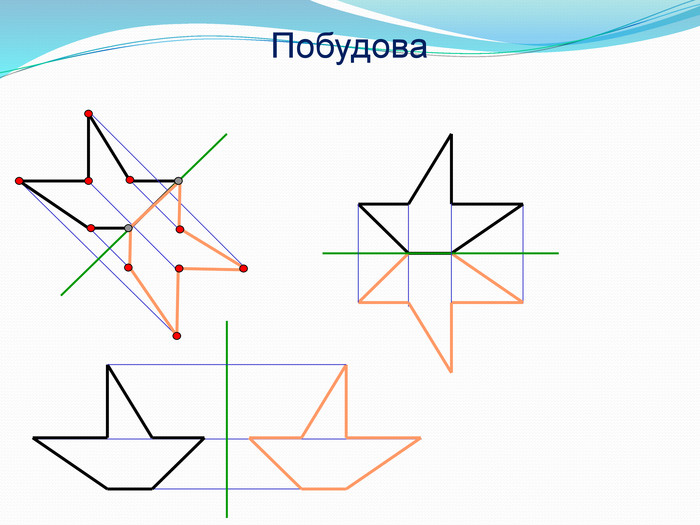
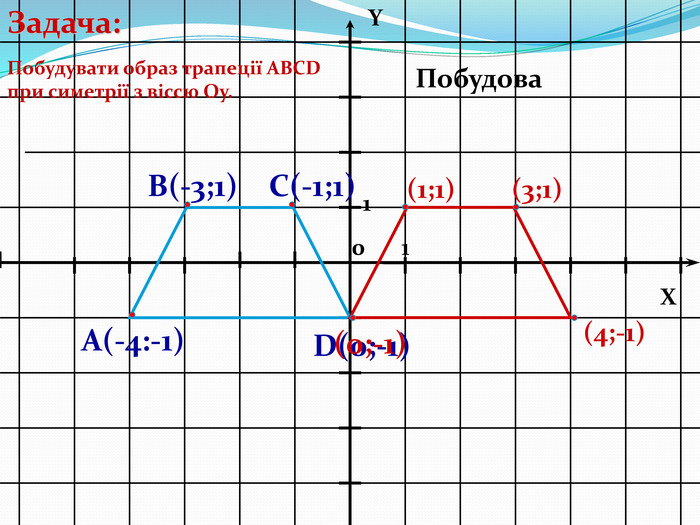
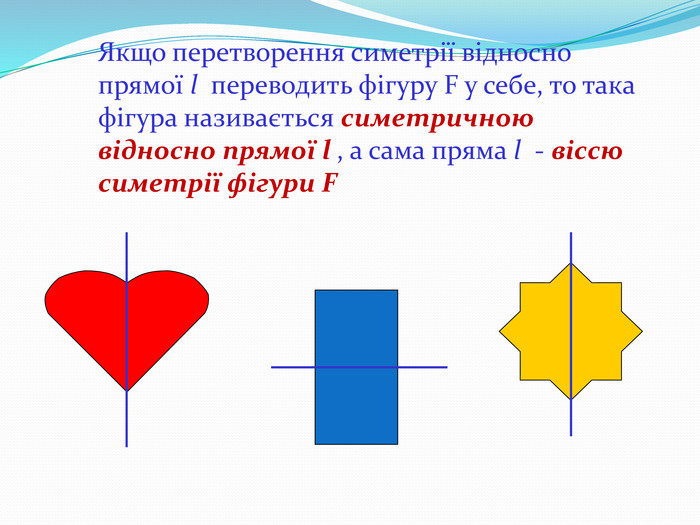
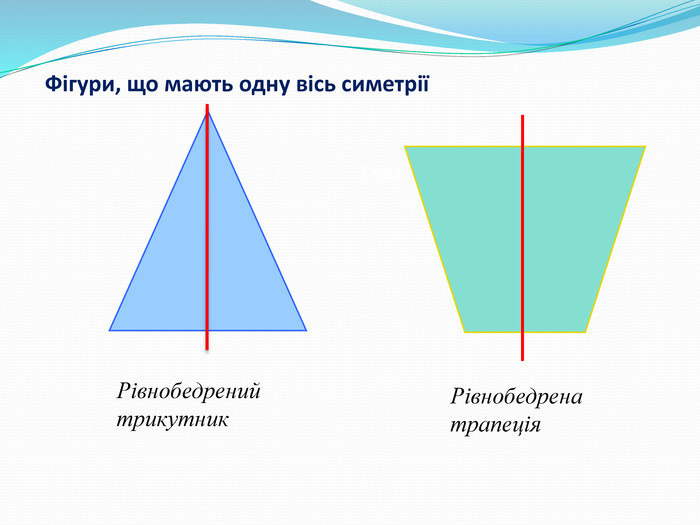
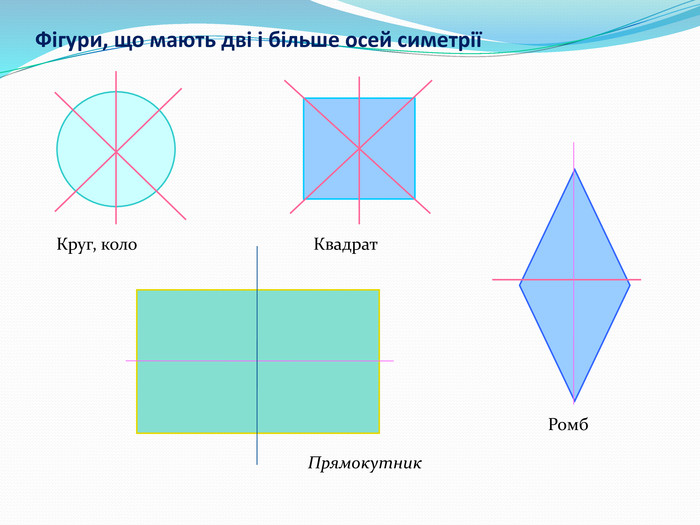
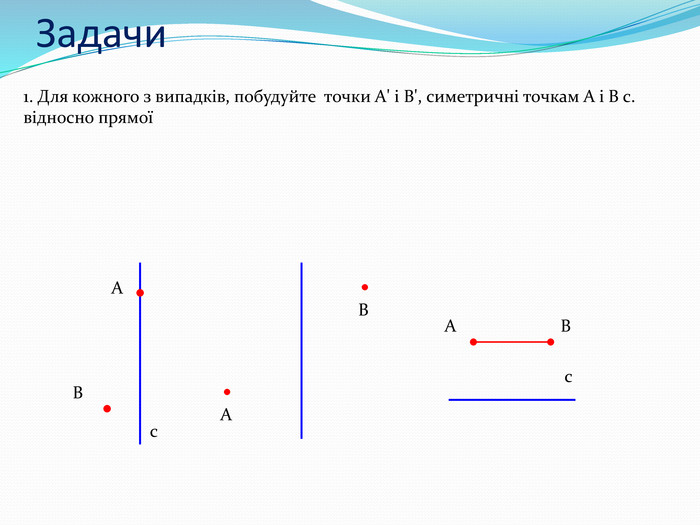
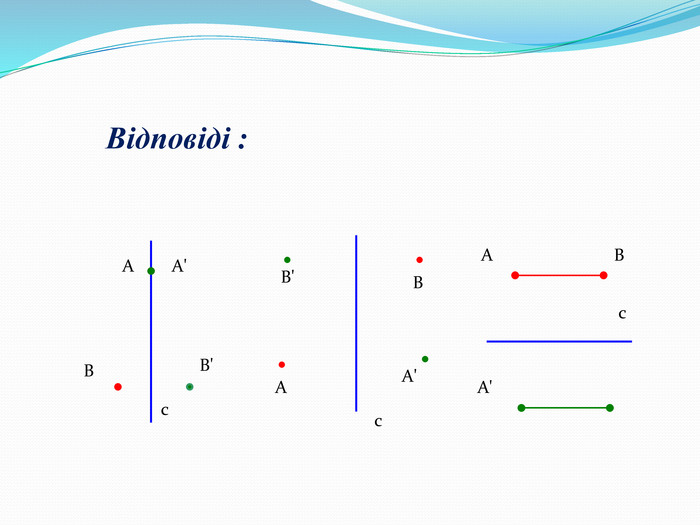
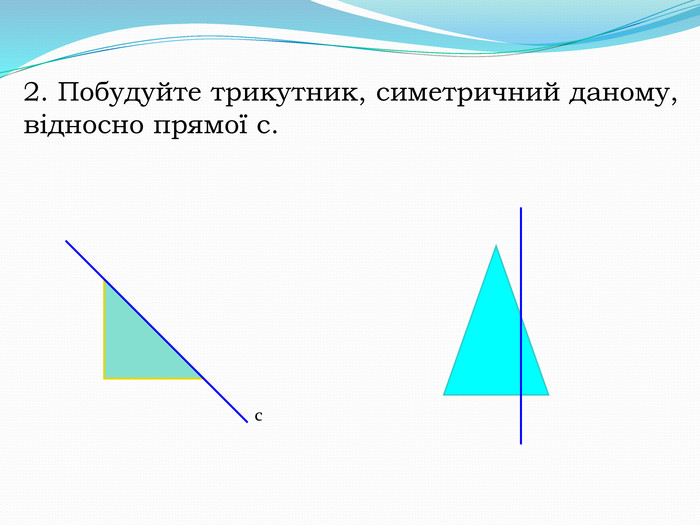
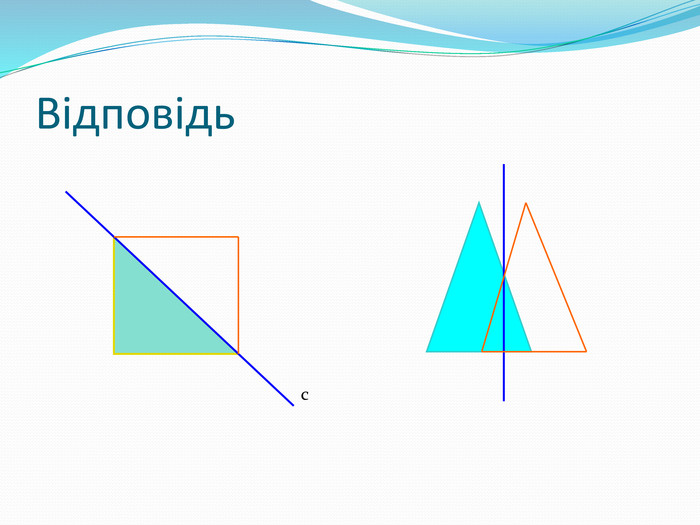
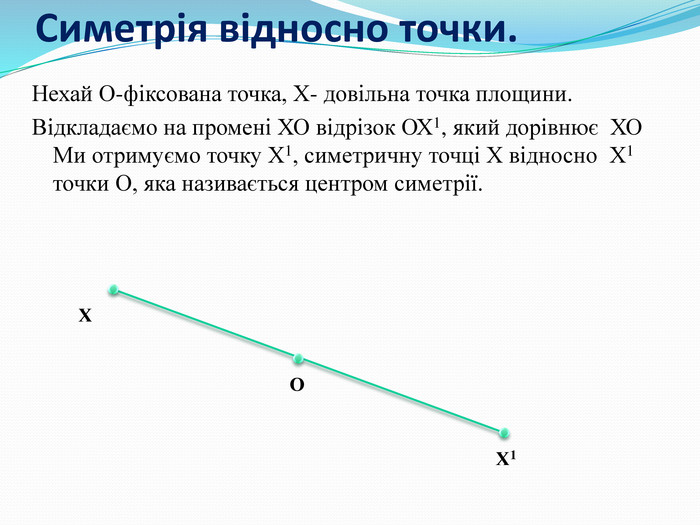
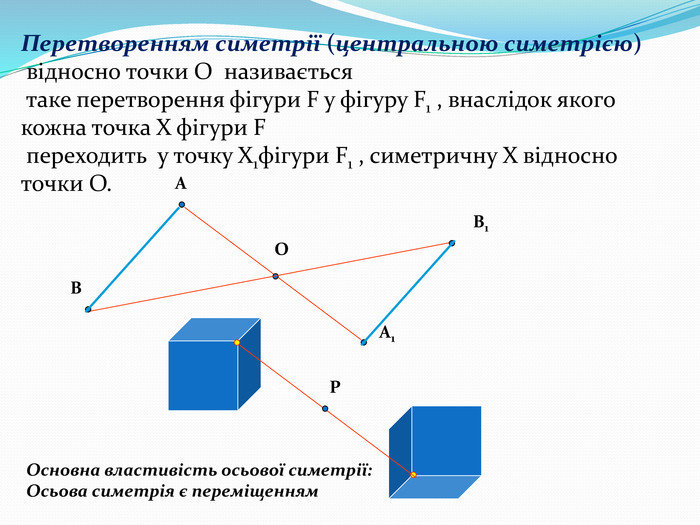
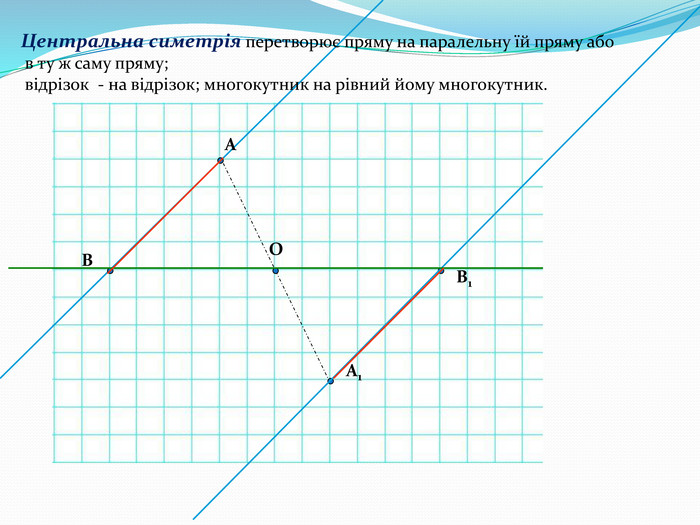
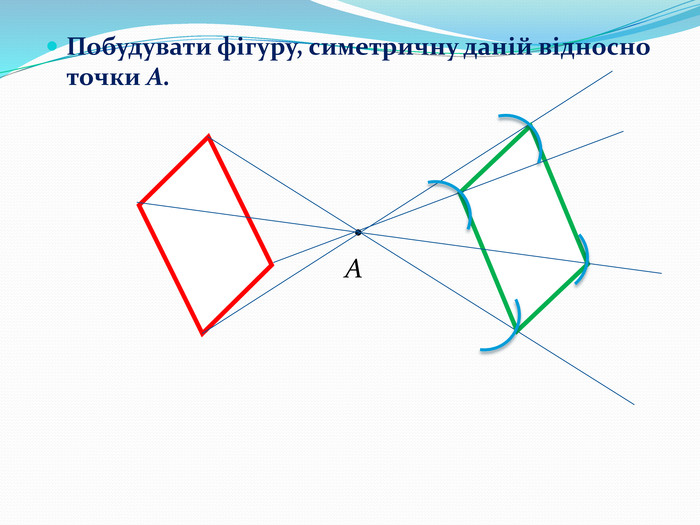
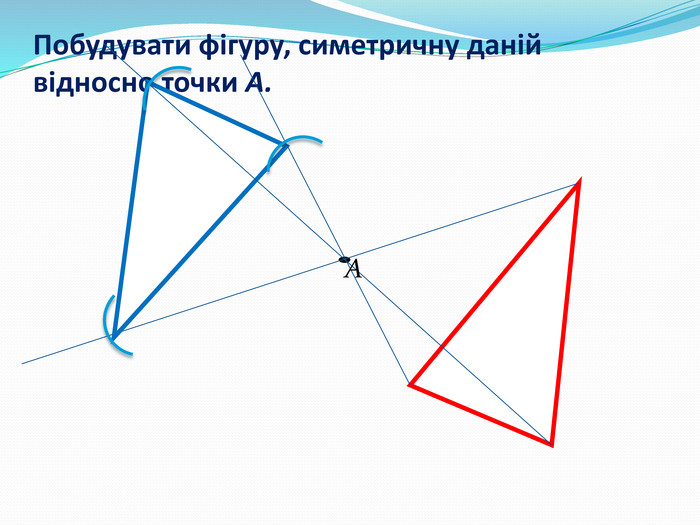
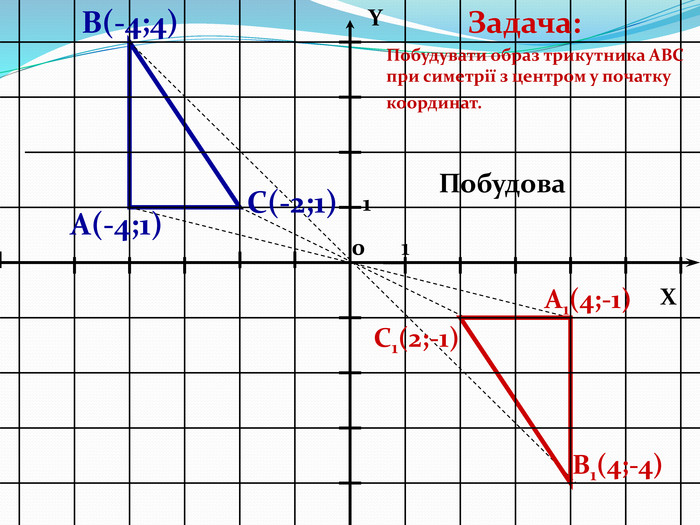
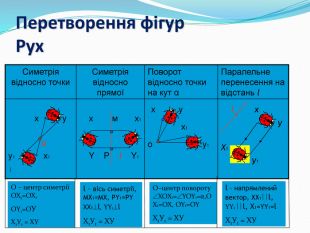
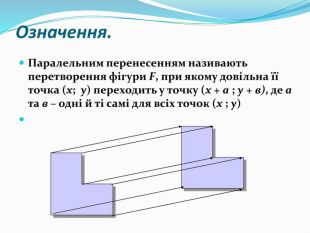
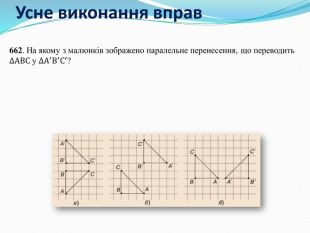
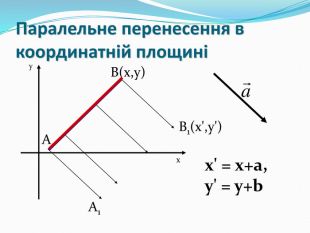
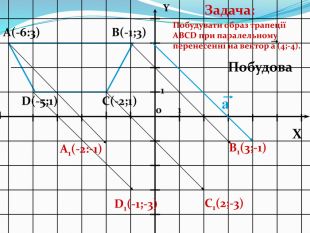
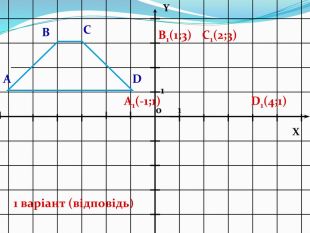
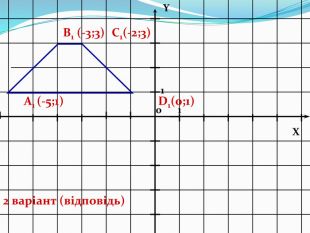
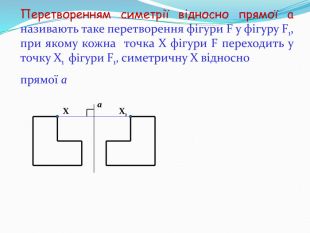
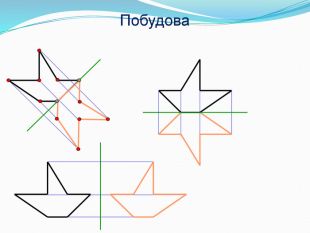
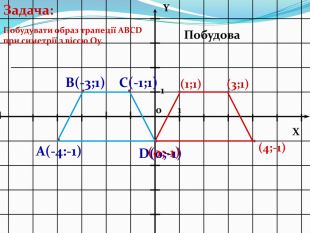
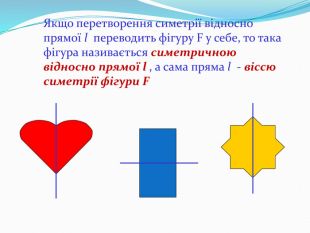
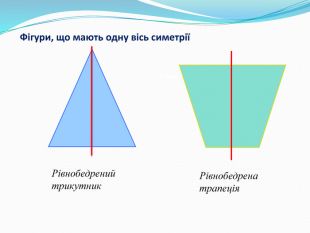
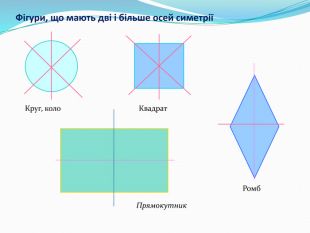
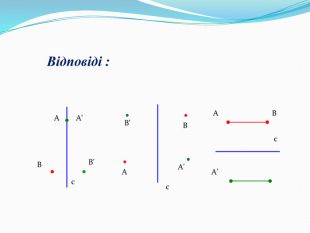
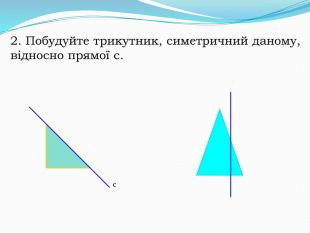
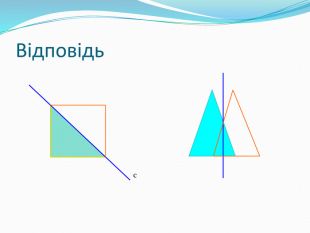
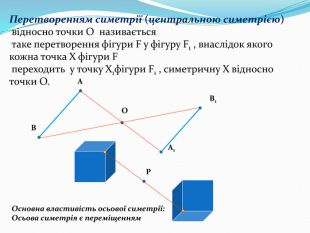
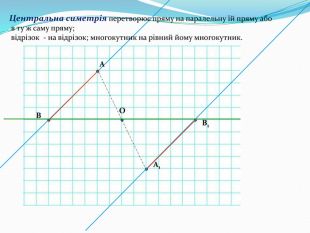
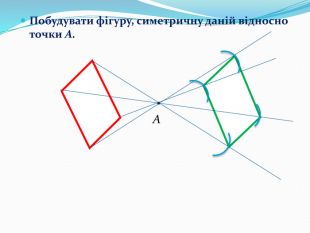
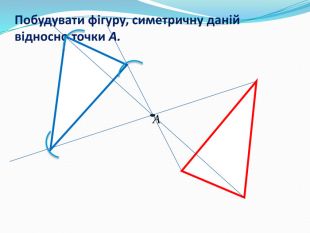
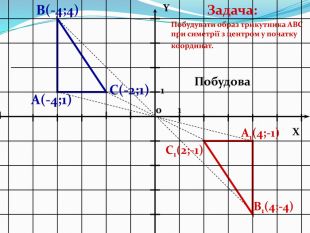
Дати поняття паралельного перенесеня, поняття осьової та центральної симетрії як властивості деяких геометричних фігур;навчити будувати симетричні точки і розпізнавати фігури , що володіють осьовою та центральною симетрією; формувати вміння і навички застосування теоретичних знань під час розв’язування задач; розширити поняття симетрії , розглянути приклади симетрії в навколишньому світі . Властивості руху в просторі.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку