Презентація "Перетворення графіків функцій"

Перетворення графіків функцій. Алгебра, 9 клас

у =kх+b, k>0хуу = х2хуху. Пряма. Парабола. Гіпербола. Графіки елементарних функційу =kх+b, k<0 Вітка параболихуу = k<0 У = ,У =,k >0

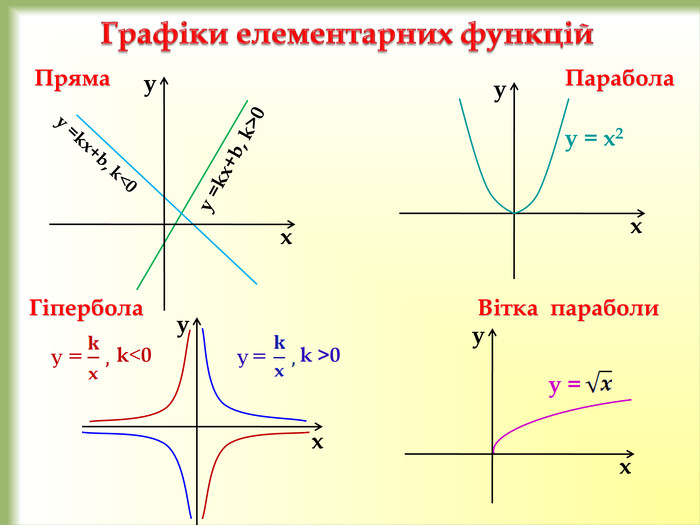
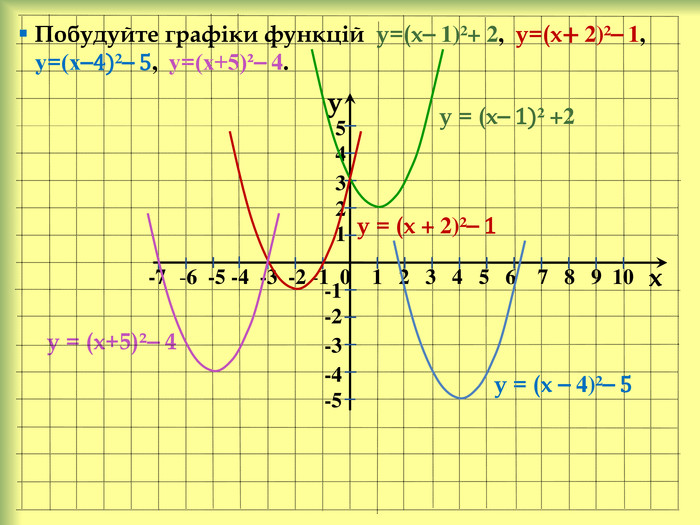
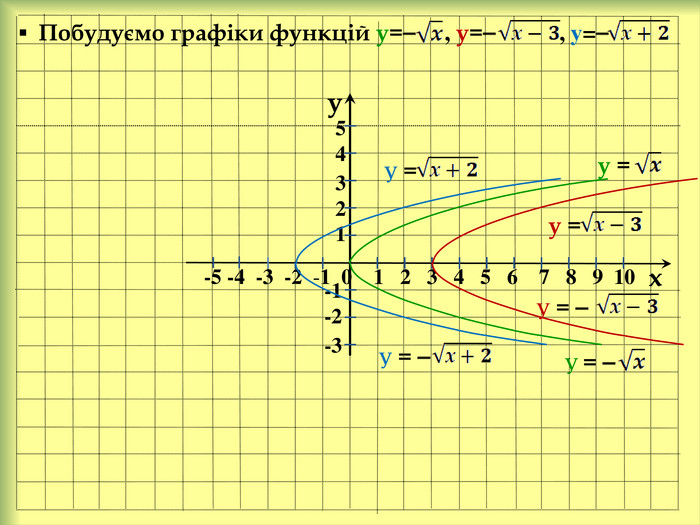
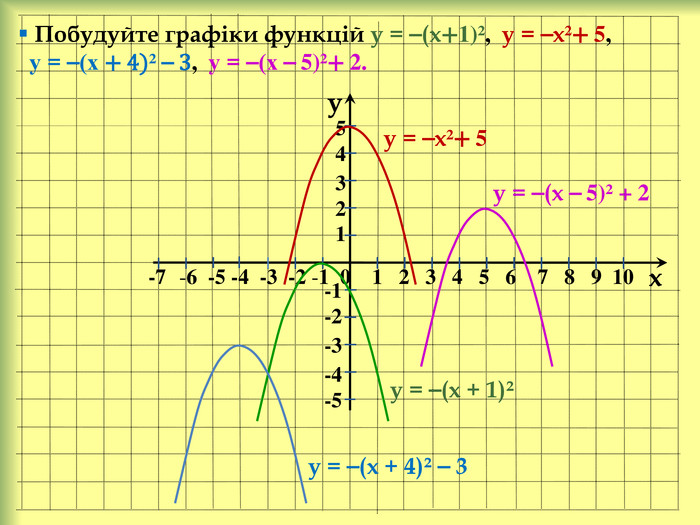
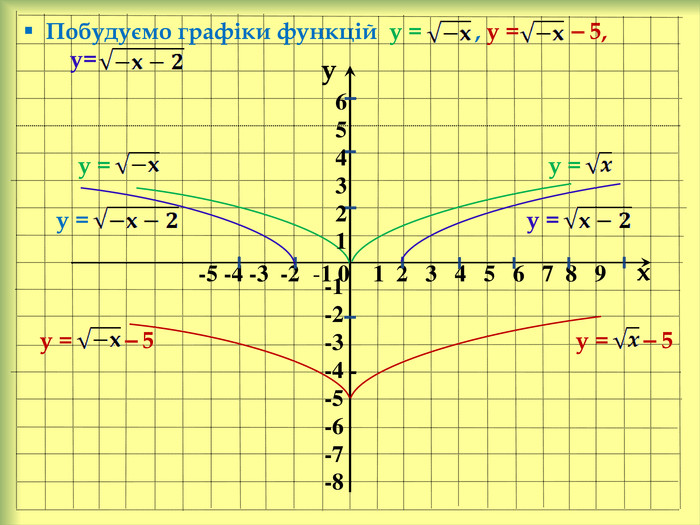
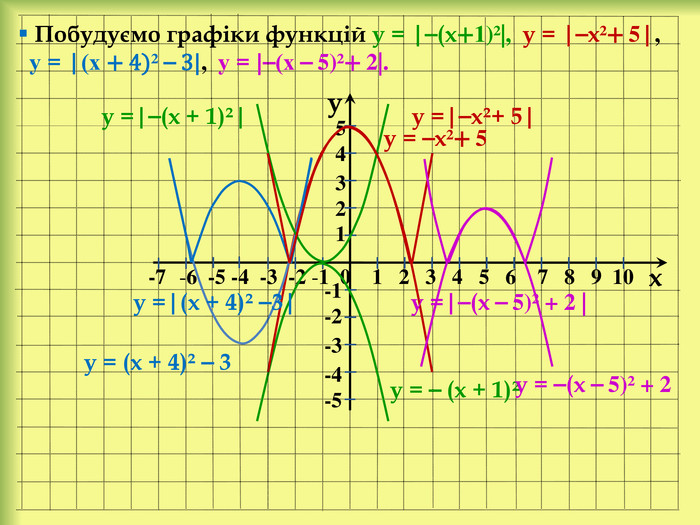
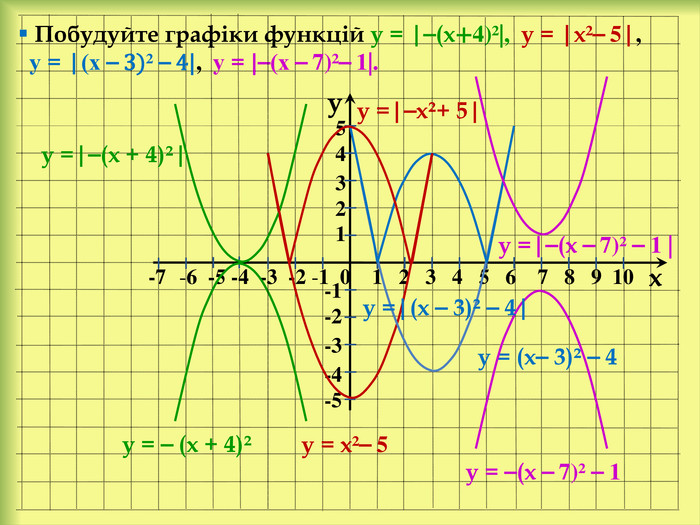
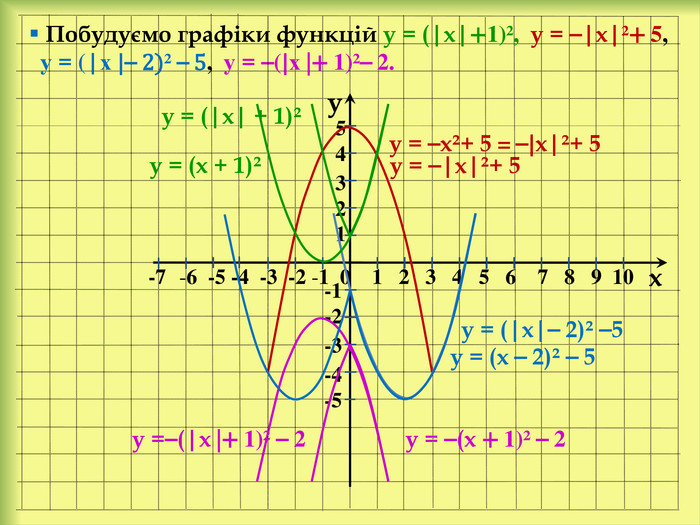
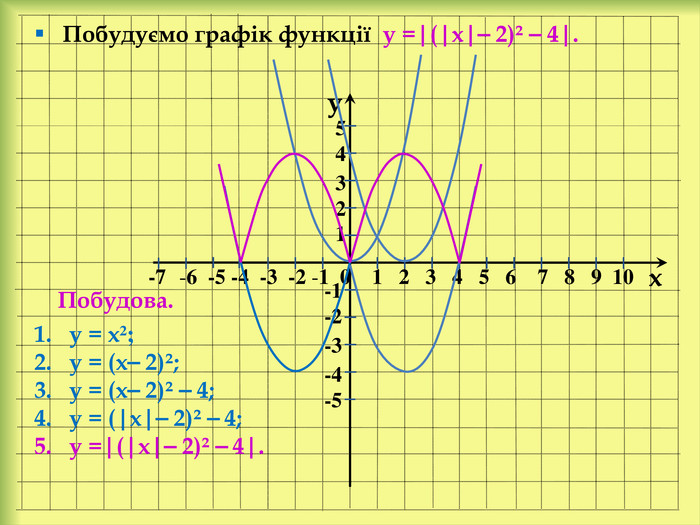
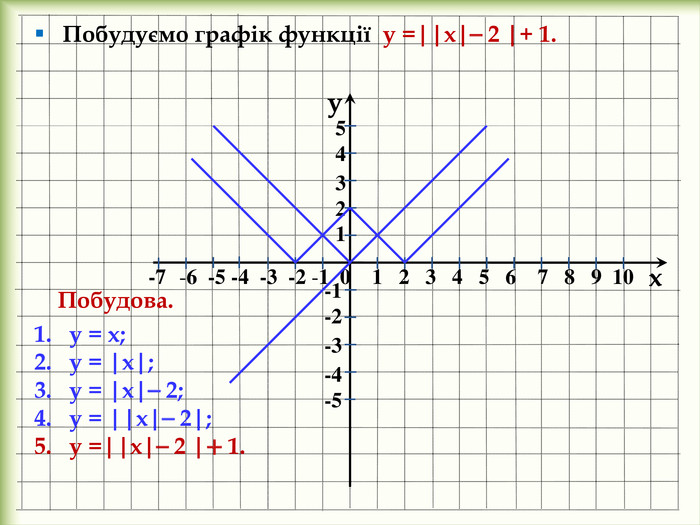
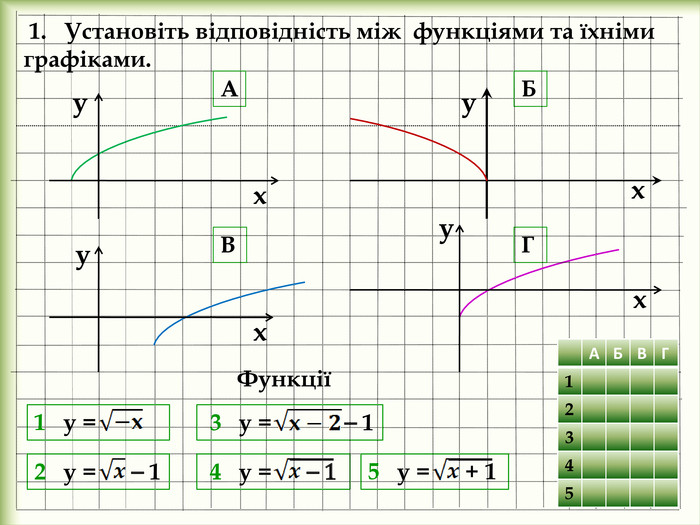
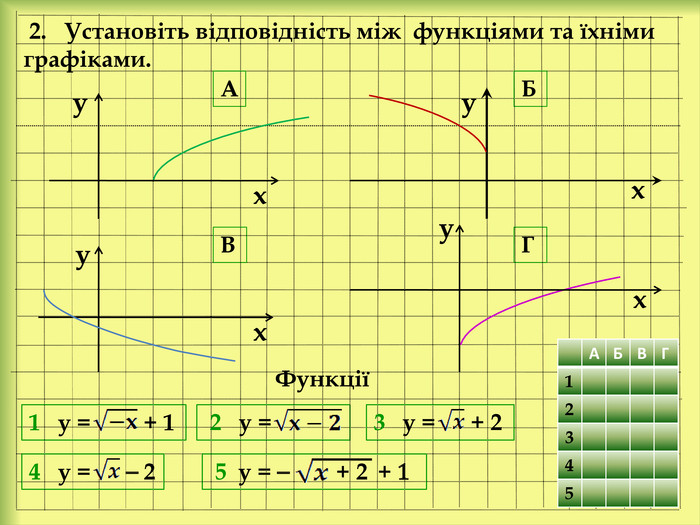
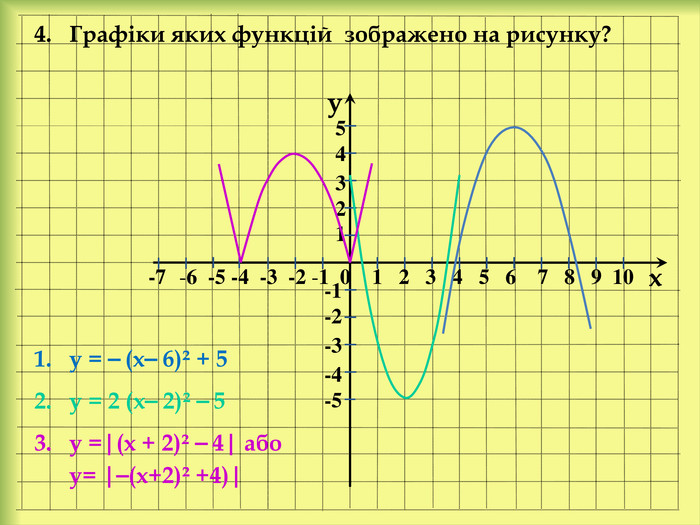
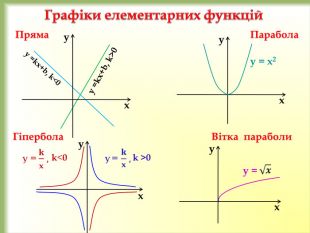
У презентації розглянемо: Графік функції у = f(x) + n, де n ˃ 0. Графік функції у = f(x + m), де m ˃ 0. Графік функції у = f(x + m) + n, де m ˃ 0, n ˃ 0. Графік функції у = ⎯f(x). Графік функції у = аf(x), де а ˃ 0. Графік функції у = f(-x). Графік функції у = |f(x)|. Графік функції у = f(|x|).

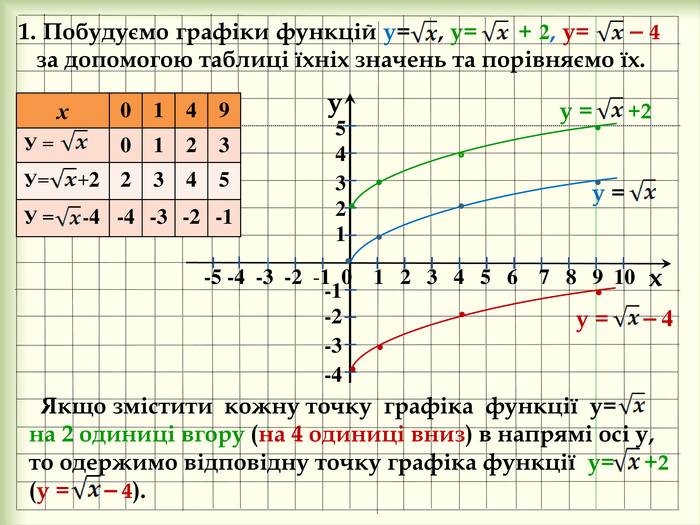
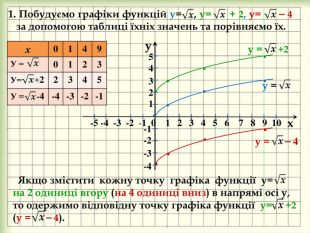
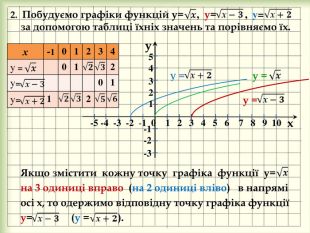
yx -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 у = -1-2-3-4у = ⎯ 4{93296810-A885-4 BE3-A3 E7-6 D5 BEEA58 F35}х0149 У = 0123 У= +22345 У = -4-4-3-2-154 321 1. Побудуємо графіки функцій у= , у= + 2, у= ⎯ 4 за допомогою таблиці їхніх значень та порівняємо їх. Якщо змістити кожну точку графіка функції у= на 2 одиниці вгору (на 4 одиниці вниз) в напрямі осі у, то одержимо відповідну точку графіка функції у= +2 (у = ⎯ 4). у = +2

1. Побудова графіка функції у = f(x) + n, де n ˃ 0. Графік функції y=f(x)+n, де n>0, можна одержати із графіка функції y=f(x) за допомогою паралельного перенесення вздовж осі у на n одиниць угору. Графік функції y=f(x)⎯n, де n>0, можна одержати із графіка функції y=f(x) за допомогою паралельного перенесення вздовж осі у на n одиниць униз.

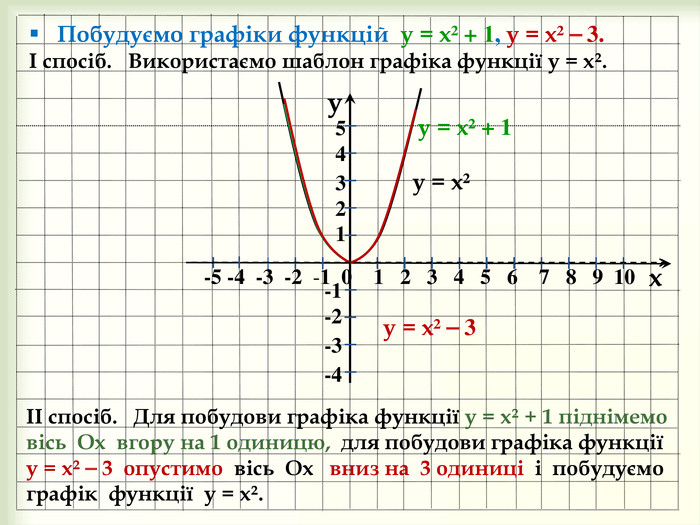
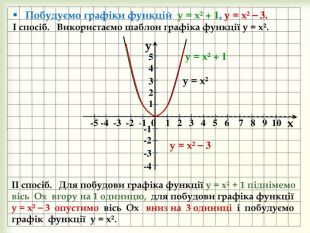
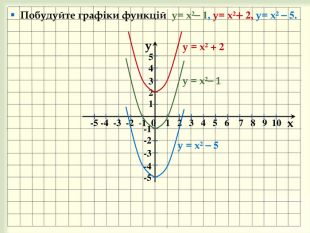
yx -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-454 321 у = х² ⎯ 3 Побудуємо графіки функцій у = х² + 1, у = х² ⎯ 3.І спосіб. Використаємо шаблон графіка функції у = х². у = х² у = х² + 1 ІІ спосіб. Для побудови графіка функції у = х² + 1 піднімемовісь Ох вгору на 1 одиницю, для побудови графіка функції у = х² ⎯ 3 опустимо вісь Ох вниз на 3 одиниці і побудуємо графік функції у = х². style.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.type

yx -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-554 321 у = х² ⎯ 5 Побудуйте графіки функцій у= х²⎯ 1, у= х²+ 2, у= х² ⎯ 5. у = х²⎯ 1 у = х² + 2

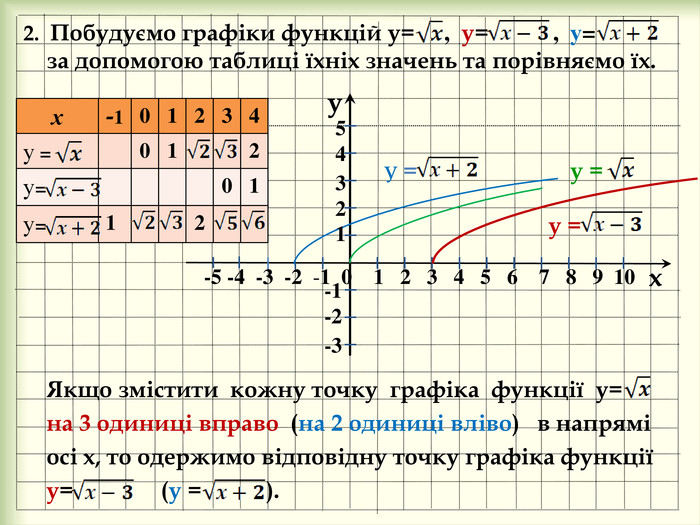
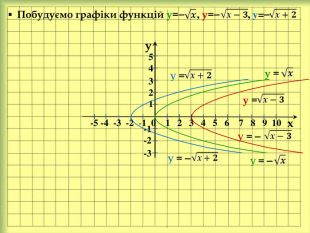
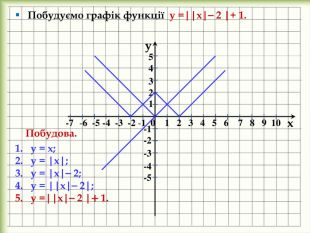
yx -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 у = -1-2-3у = {93296810-A885-4 BE3-A3 E7-6 D5 BEEA58 F35}х-101234у =012у=01у=1254 3212. Побудуємо графіки функцій у= , у= , у= за допомогою таблиці їхніх значень та порівняємо їх. Якщо змістити кожну точку графіка функції у= на 3 одиниці вправо (на 2 одиниці вліво) в напрямі осі х, то одержимо відповідну точку графіка функції у= (у = ). У =

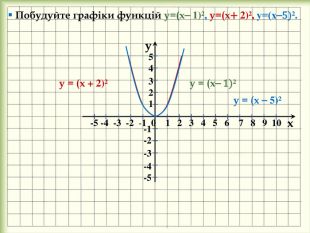
2. Побудова графіка функції у= f(x + m), де m ˃ 0. Графік функції y = f(x⎯m), де m > 0, можна одержати із графіка функції y= f(x) за допомогою паралельного перенесення вздовж осі x на m одиниць праворуч. Графік функції y = f(x+m), де m > 0, можна одержати із графіка функції y= f(x) за допомогою паралельного перенесення вздовж осі x на m одиниць ліворуч.

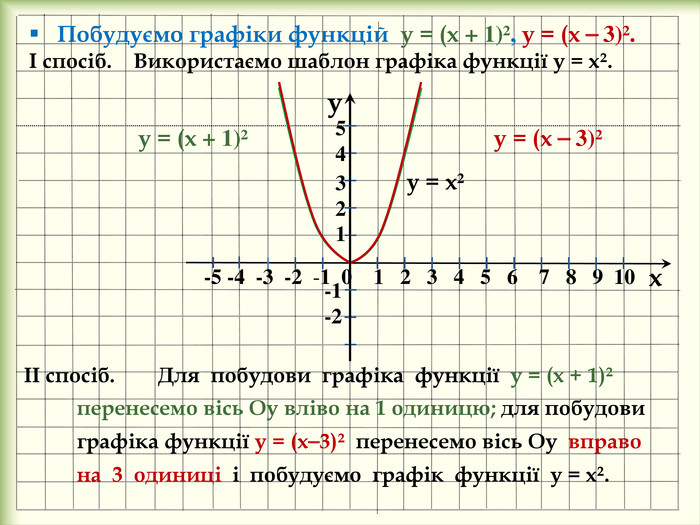
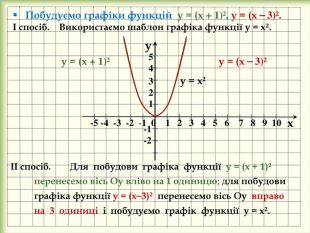
yx -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-254 321 Побудуємо графіки функцій у = (х + 1)², у = (х ⎯ 3)².І спосіб. Використаємо шаблон графіка функції у = х². у = х² у = (х + 1)² ІІ спосіб. Для побудови графіка функції у = (х + 1)² перенесемо вісь Оу вліво на 1 одиницю; для побудови графіка функції у = (х⎯3)² перенесемо вісь Оу вправо на 3 одиниці і побудуємо графік функції у = х². у = (х ⎯ 3)² style.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.type

yx -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-554 321 Побудуйте графіки функцій у=(х⎯ 1)², у=(х+ 2)², у=(х⎯5)². у = (х⎯ 1)² у = (х + 2)² у = (х ⎯ 5)²

3. Побудова графіка функції y= f(x ± m) ± n, де m > 0 і n > 0. Графік функції y= f(x ± m) ± n, де m > 0 і n > 0, можна одержати із графіка функції y= f(x) за допомогою паралельного перенесення вздовж осі x на m одиниць ліворуч (праворуч), а потім уздовж осі у на n одиниць вгору (вниз).

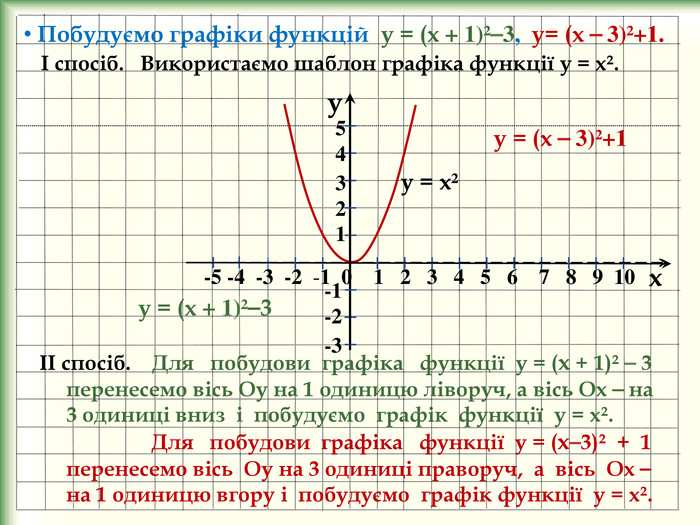
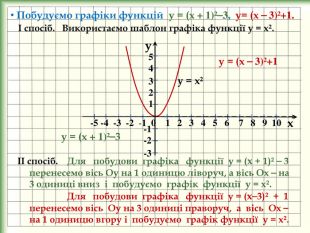
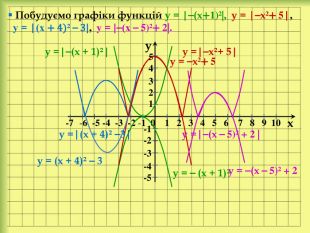
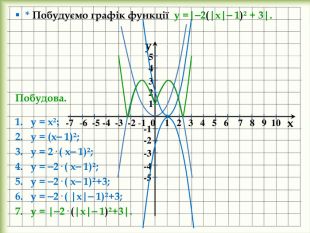
yx -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-354 321 Побудуємо графіки функцій у = (х + 1)²⎯3, у= (х ⎯ 3)²+1. І спосіб. Використаємо шаблон графіка функції у = х². у = х² у = (х + 1)²⎯3 ІІ спосіб. Для побудови графіка функції у = (х + 1)² ⎯ 3 перенесемо вісь Оу на 1 одиницю ліворуч, а вісь Ох ⎯ на 3 одиниці вниз і побудуємо графік функції у = х². Для побудови графіка функції у = (х⎯3)² + 1 перенесемо вісь Оу на 3 одиниці праворуч, а вісь Ох ⎯ на 1 одиницю вгору і побудуємо графік функції у = х². у = (х ⎯ 3)²+1 stroke.colorstroke.onstyle.colorfillcolorstroke.colorfill.type

yx у = (х+5)²⎯ 4 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-554 321 Побудуйте графіки функцій у=(х⎯ 1)²+ 2, у=(х+ 2)²⎯ 1, у=(х⎯4)²⎯ 5, у=(х+5)²⎯ 4. у = (х⎯ 1)² +2 у = (х + 2)²⎯ 1 у = (х ⎯ 4)²⎯ 5

4. Побудова графіка функції y = ⎯f(x) Графік функції y= ⎯f(x) можна одержати із графіка функції y=f(x) за допомогою симетрії відносно осі х.

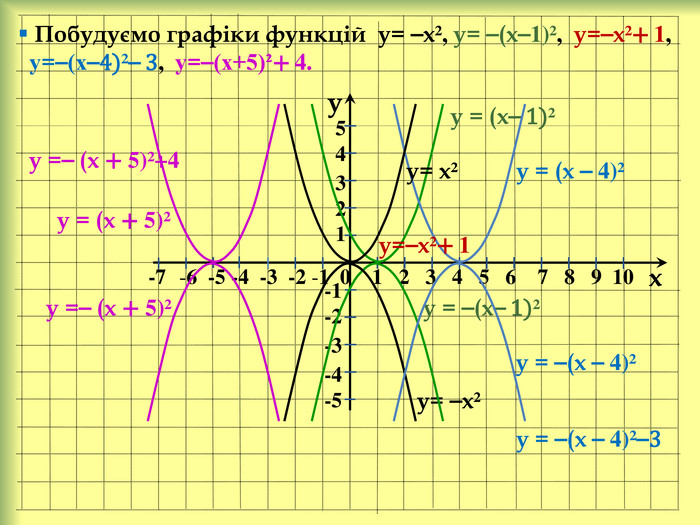
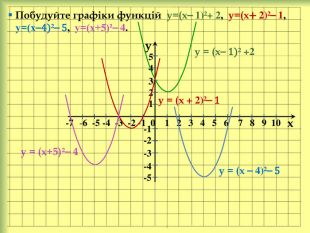
yx -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-554 321 Побудуємо графіки функцій у= ⎯х², у= ⎯(х⎯1)², у=⎯х²+ 1, у=⎯(х⎯4)²⎯ 3, у=⎯(х+5)²+ 4. у = (х⎯ 1)² у = (х ⎯ 4)² у= х² у= ⎯х² у = ⎯(х⎯ 1)² у=⎯х²+ 1у = ⎯(х ⎯ 4)² у = ⎯(х ⎯ 4)²⎯3 у = (х + 5)² у =⎯ (х + 5)² у =⎯ (х + 5)²+4 stroke.colorstroke.on

yx -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 у = -1-2-3у = 54 321 Побудуємо графіки функцій у=⎯ , у=⎯ , у=⎯ У =У = ⎯ У = ⎯У = ⎯

yx -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-554 321 Побудуйте графіки функцій у = ⎯(х+1)², у = ⎯х²+ 5, у = ⎯(х + 4)² ⎯ 3, у = ⎯(х ⎯ 5)²+ 2. у = ⎯(х + 1)² у = ⎯х²+ 5 у = ⎯(х + 4)² ⎯ 3 у = ⎯(х ⎯ 5)² + 2

5. Побудова графіка функції y=а·f(x), де а > 0. Графік функції y=а·f(x), де а > 0, можна одержати із графіка функції y=f(x), розтягнувши від осі х в а разів, якщо а > 1, і стиснувши його до осі х в 1/а разів, якщо 0 < а < 1.

yx -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-5-654 321 Побудуємо графіки функцій у= ⎯2х², у= ⎯3х², у= ⎯½х², у= ⎯¼х². Побудуємо графіки функцій у=2х², у=3х², у=½х², у=¼х². у = х² у = 3х ²у = ½· х ²у = 2х² у=¼· х² у = ⎯2х² у = ⎯3х ²у = ⎯½· х ²у=⎯¼· х²

6. Побудова графіка функції y = f(⎯x). Графік функції y = f(⎯x) можна одержати із графіка функції y = f(x), відобразивши його симетрично відносно осі у.

yx -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 у = у = 654 321-1-2-3-4 - -5-6-7-8у = ⎯ 5 Побудуємо графіки функцій у = , у = ⎯ 5, у=у = ⎯ 5у = у =

7. Побудова графіка функції у = |f(x)|. Графік функції y =|f(x)| можна одержати із графіка функції y = f(x), відобразивши симетрично відносно осі х ту його частину, що розташована нижче від цієї осі х.

yx -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-554 321 Побудуємо графіки функцій у = |⎯(х+1)²|, у = |⎯х²+ 5|, у = |(х + 4)² ⎯ 3|, у = |⎯(х ⎯ 5)²+ 2|. у = ⎯ (х + 1)² у = ⎯х²+ 5 у = (х + 4)² ⎯ 3 у = ⎯(х ⎯ 5)² + 2 у =|⎯х²+ 5| у =|⎯(х + 1)²| у =|(х + 4)² ⎯3| у =|⎯(х ⎯ 5)² + 2 |

yx -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-554 321 Побудуйте графіки функцій у = |⎯(х+4)²|, у = |х²⎯ 5|, у = |(х ⎯ 3)² ⎯ 4|, у = |⎯(х ⎯ 7)²⎯ 1|. у = ⎯ (х + 4)² у = х²⎯ 5 у = (х⎯ 3)² ⎯ 4 у = ⎯(х ⎯ 7)² ⎯ 1 у =|⎯х²+ 5| у =|⎯(х + 4)²| у =|(х ⎯ 3)² ⎯ 4| у =|⎯(х ⎯ 7)² ⎯ 1 |

8. Побудова графіка функції у = f (|x|). Графік функції y = f(|x|) можна одержати із частини графіка функції y = f(x), побудованого для х > 0 та симетричної цій частині графіка відносно осі у.

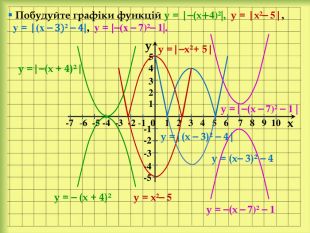
yx -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-554 321 Побудуємо графіки функцій у = (|х|+1)², у = ⎯|х|²+ 5, у = (|х |⎯ 2)² ⎯ 5, у = ⎯(|х |+ 1)²⎯ 2. у = (х + 1)² у = ⎯х²+ 5 = ⎯|х|²+ 5 у = (х ⎯ 2)² ⎯ 5 у = ⎯(х + 1)² ⎯ 2 у = ⎯|х|²+ 5 у = (|х| + 1)² у = (|х|⎯ 2)² ⎯5 у =⎯(|х |+ 1)² ⎯ 2

yx -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-554 321 Побудуємо графік функції у =|(|х|⎯ 2)² ⎯ 4|. Побудова.у = х²;у = (х⎯ 2)²;у = (х⎯ 2)² ⎯ 4;у = (|х|⎯ 2)² ⎯ 4;у =|(|х|⎯ 2)² ⎯ 4|.

yx -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-554 321 Побудуємо графік функції у =||х|⎯ 2 |+ 1. Побудова.у = х;у = |х|;у = |х|⎯ 2;у = ||х|⎯ 2|;у =||х|⎯ 2 |+ 1. stroke.colorstroke.onstroke.colorstroke.onstroke.colorstroke.onstroke.colorstroke.on

yx -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-554 321 * Побудуємо графік функції у =|⎯2(|х|⎯ 1)² + 3|. Побудова.у = х²;у = (х⎯ 1)²;у = 2· ( х⎯ 1)²;у = ⎯2· ( х⎯ 1)²;у = ⎯2· ( х⎯ 1)²+3;у = ⎯2· ( |х|⎯ 1)²+3;у = |⎯2· (|х|⎯ 1)²+3|.

Самостійна робота

yx 5 у = + 1 2 у = ⎯ 1 1. Установіть відповідність між функціями та їхніми графіками. 4 у = ⎯ 1 3 у = ⎯ 11 у = xyxxyy. АБВГ{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГ1 Х2 Х3 Х45 ХФункції{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГ12345

yx 3 у = + 2 4 у = ⎯ 2 2. Установіть відповідність між функціями та їхніми графіками. 5 у = ⎯ + 2 + 1 2 у = 1 у = + 1xyxxyy. АБВГ{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГ1 Х2 Х34 Х5 ХФункції{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГ12345

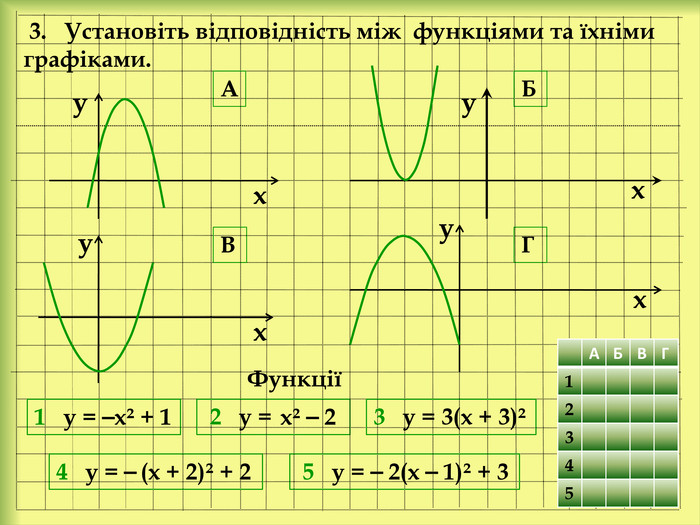
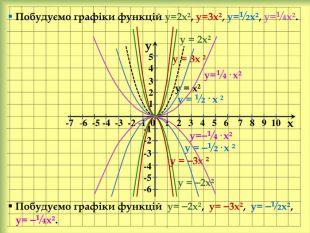
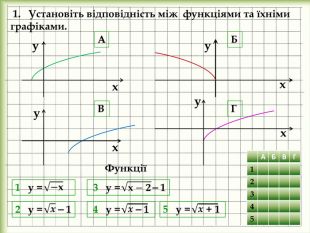
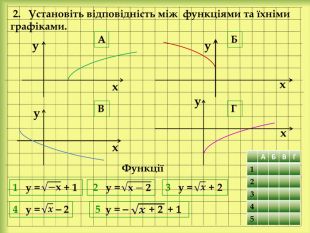
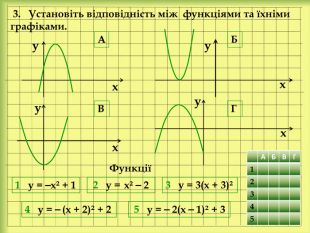
yx 3 у = 3(х + 3)² 4 у = ⎯ (х + 2)² + 2 3. Установіть відповідність між функціями та їхніми графіками. 5 у = ⎯ 2(х ⎯ 1)² + 3 2 у = 1 у = ⎯х² + 1xyxxyy. АБВГ{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГ12 Х3 Х4 Х5 ХФункції{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГ12345х² ⎯ 2

yx -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 -1-2-3-4-554 321 4. Графіки яких функцій зображено на рисунку? у = ⎯ (х⎯ 6)² + 5у = 2 (х⎯ 2)² ⎯ 5у =|(х + 2)² ⎯ 4| або у= |⎯(х+2)² +4)|