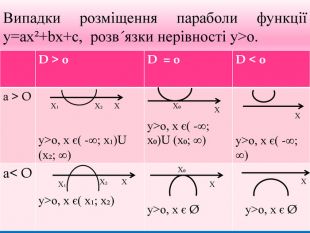
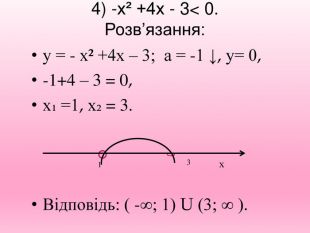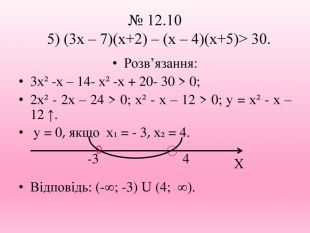Презентація. "Розв'язування квадратних нерівностей з параметрами"
Про матеріал
Матеріал відповідає класичній схемі вивчення розв'язування квадратних нерівностей з параметрами. Наведено ряд завдань, які вимагають досить глибокого володіння теоретичним матеріалом розв'язування квадратних нерівностей. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


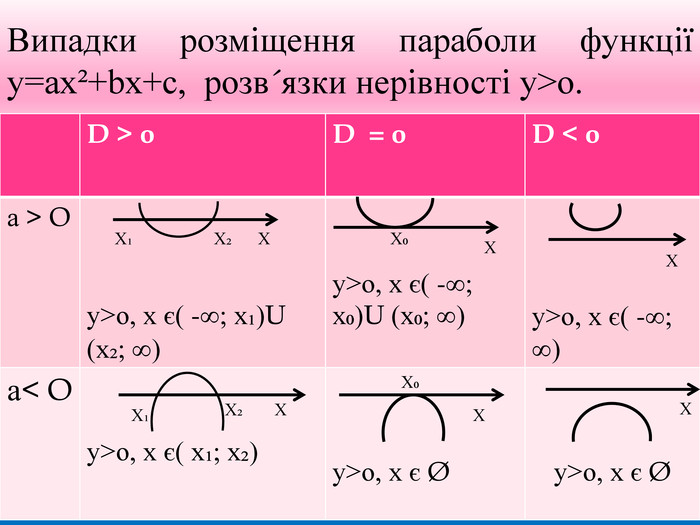

![5) 3х² - 7х +4≤ 0. Розв’язання.у = 3х² - 7х +4, а = 3 >0↑, у= 0 , х₁= 1;х₂ = 1⅓. Відповідь: [ 1; 1 ⅓].1⅓Х1 5) 3х² - 7х +4≤ 0. Розв’язання.у = 3х² - 7х +4, а = 3 >0↑, у= 0 , х₁= 1;х₂ = 1⅓. Відповідь: [ 1; 1 ⅓].1⅓Х1](/uploads/files/834524/183678/196283_images/6.jpg)
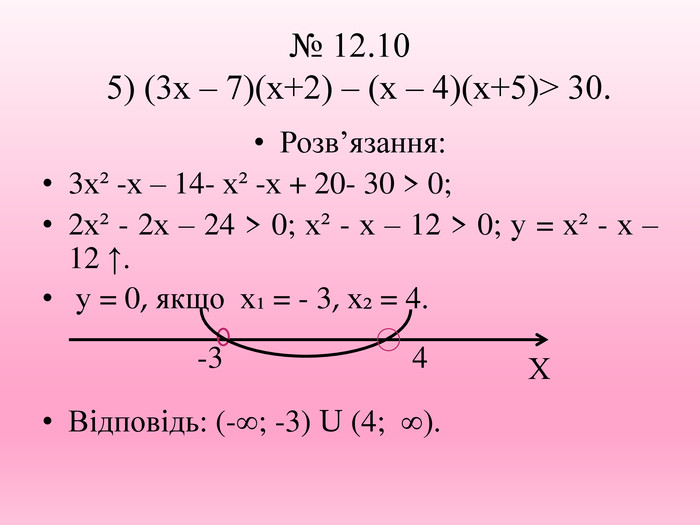




![Розв´язуванняа> 0, а >0, а >0,D ≤ 0, (а-1)² -4а (а-1)≤ 0, (а -1) (а-1-4а)≤ 0,а > 0,(а-1)(3а+1)≥ 0. q(а)=0, а=1, а=-⅓, ↑.а >0,а є (-∞; -⅓]U[1;∞). а є [1;∞). Відповідь: а є [1;∞).1а-⅓0 Розв´язуванняа> 0, а >0, а >0,D ≤ 0, (а-1)² -4а (а-1)≤ 0, (а -1) (а-1-4а)≤ 0,а > 0,(а-1)(3а+1)≥ 0. q(а)=0, а=1, а=-⅓, ↑.а >0,а є (-∞; -⅓]U[1;∞). а є [1;∞). Відповідь: а є [1;∞).1а-⅓0](/uploads/files/834524/183678/196283_images/12.jpg)