Презентація ,,Підготовка до ЗНО.Прогресії''
Про матеріал
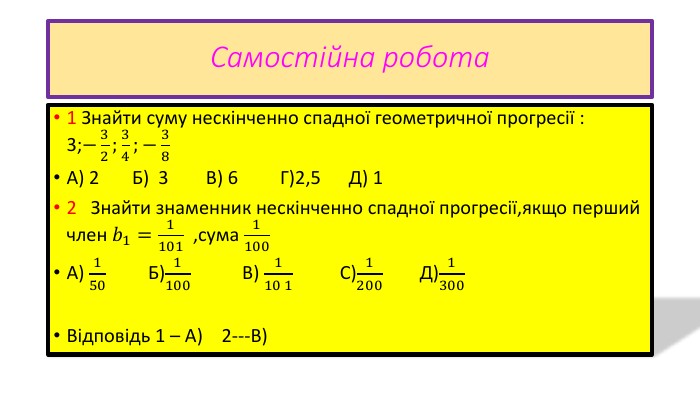
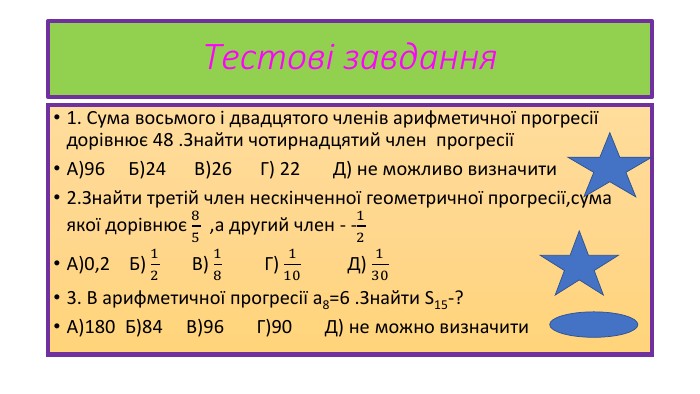
Презентація доможе при повторенні матеріалу о прогресіях при підготовці до ЗНО.Презентація розрахована на 11 клас рівень стандарту. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку