Презентація "Піфагор і його теорема" 8 кл.
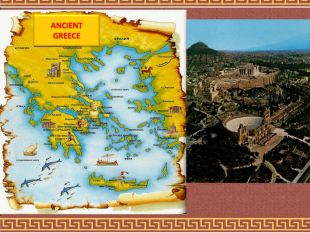
Історія людини, в якій переплелися легенди та реалії - це опис життя славетного грецького математика, відомого нам як Піфагор. Геометрія володіє двома скарбами: один з них - теорема Піфагора.
























Давньогрецькі математики Завдяки визначним досягненням давньогрецьких математиків і було створено науково-теоретичний грунт, на якому наступні покоління вчених розвивали математику. Найдавнішими з грецьких учених був Фалес Мілетський, Піфагор, Евклід, Архімед, Рене Декарт та ін. Фалес Мілетський. Евклід. Архімед
Древньогрецький філософ і математик, основоположник релігійно-філософської школи піфагорійців.Історію життя Піфагора важко відділити від легенд, що показують його в якості неперевершеного мудреця. Ще древній історик Геродот називав його «найвеличнішим елінським мудрецем». Піфагор Самоський (570—490 рр. до н. е.)
Легенда про народження Піфагора. В VI столітті до нашої ери осередком грецької науки та мистецтва стала Іонія. Там у сім’ї золотих справ майстра Мнесарха народився син. За легендою, в Дельтах, куди приїхали Мнесарх з дружиною Парфенісою, оракул пророчив їм народження сина, який буде славитися віками своєю мудрістю, справами та красою. Бог Аполлон, вустами оракула, радить їм плисти в Сірію. Пророцво збувається - в Сидоні Парфеніса народила хлопчика. І тоді за давньою традицією Парфеніса приймає ім’я Піфіада, на честь Аполлона Піфійського, а сина називає Піфагором, на честь пророцтва.
Дитинство Піфагора. Як і будь-який батько, Мнесарх мріяв, що син буде продовжувати його справу-ремесло золотих справ майстра. Життя вирішило інакше. Майбутній математик та філософ вже в дитинстві виявив велику здатність до наук. У свого першого вчителя Гермодамаса Піфагор отримує знання основ музики та живопису. Для покращення пам’яті Гермодамас примушував його вивчати пісні з “Одіссеї” та “Іліади”. Перший вчитель навчив Піфагора любити природу та вивчати її таємниці.
Вперед до Єгипту!Пройшло кілька років, і за порадою свого вчителя Піфагор вирішує продовжити навчання в Єгипті. По дорозі відбувається знайомство Піфагора з філософом Ферекідом- другом Фалеса. У Ферекіда Піфагор навчається астрології, таємницям чисел, медицині та іншим обов’язковим на той час наукам. Згодом шлях Піфагора лежить у Мілет до відомого Фалеса, засновника першої в історії філософської школи.
Піфагор у полоніНавчання Піфагора в Єгипті сприяє тому, що він стає одним із найбільш освічених людей свого часу. До цього періоду відноситься подія, яка змінила все його майбутнє життя. Помер фараон, а його наступник по трону не сплатив щорічну данину персидському царю. Перси не помилували навіть священні храми. Піддалися гонінням і жреці: їх вбивали або брали в полон. Так потрапив у персидський полон і Піфагор.
Повернення на Батьківщину. Дванадцять років знаходився у вавилонському полоні Піфагор, доки його не звільнив персидський цар Дарій Гістасп, прочувший про відомого грека. Піфагору вже 60, він вирішує повернутися батьківщину, щоб прилучити до набутих знань свій народ. Досить швидко він здобуває велику популярність серед населення. Ентузіазм населення настільки великий, що навіть дівчата та жінки порушували закон, що забороняв їм знаходитися на зборах. Досконало володіючи методами єгипетських жреців, Піфагор “очищував душі своїх слухачів, вигоняв вади з серця та наповнював уми світлою правдою”.
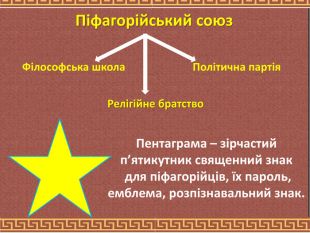
12 Це був одночасно і релігійний союз, і політичний клуб, і наукове товариство. Учні цієї школи зобов’язувались вести так званий піфагорійський спосіб життя. Статут піфагорійського союзу був дуже суворим. Кожний, хто вступав до нього, відмовлявся від особистої власності на користь союзу, зобов’язувався не проливати крові, не вживати м’ясної їжі, берегти таємницю вчення свого вчителя.
Відкриття піфагорійців Піфагорійцями було зроблено багато важливих відкриттів в арифметиці і геометрії, в тому числі:теорема про суму внутрішніх кутів трикутника;побудова правильних багатокутників і ділення площині на деякі з них;геометричні способи розв'язання квадратних рівнянь;розподіл чисел на парні і непарні, прості і складові; створена математична теорія музики
В Золотих віршах Піфагор показав ті моральні правила, суворе виконання яких призводить душі до ідеалу . Ось кілька з них: Не роби ніколи того, що не знаєш. Але вчись усьому, що потрібно знати, і тоді будеш вести спокійне життя. Не зневажай здоров’ям свого тіла. Давай йому вчасно їжу і пиття, і вправи в яких воно потребує. Привчайся жити просто. Не зачиняй очей, коли хочеш спати, не розглянувши усіх своїх вчинків у минулий день.
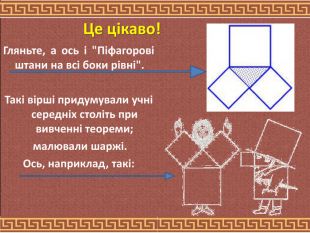
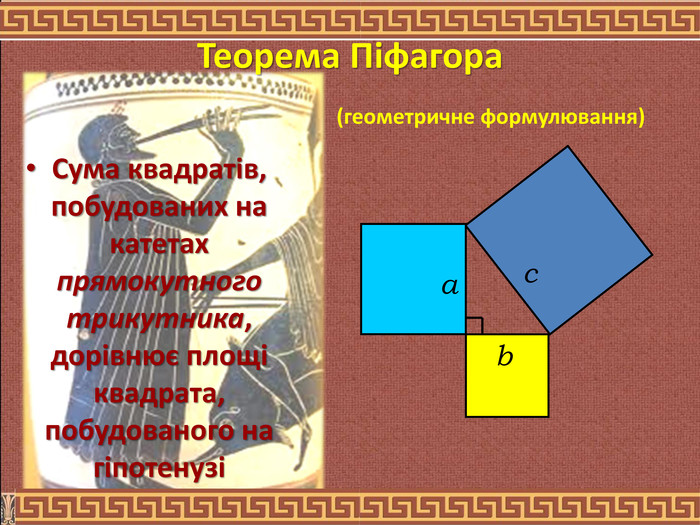
Доведення теореми Піфагора. З давнини математики знаходять все нові і нові доведення теореми Піфагора. Таких доведень - більш менш чітких та наочних – відомо 370, але бажання знайти нові збереглось до наших часів. Самостійні “відкриття” доведень теореми Піфагора будуть корисними і сучасним школярам. Теорема Піфагора
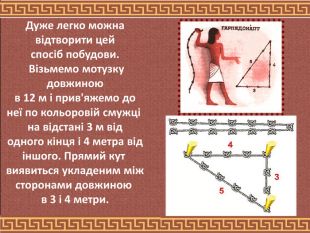
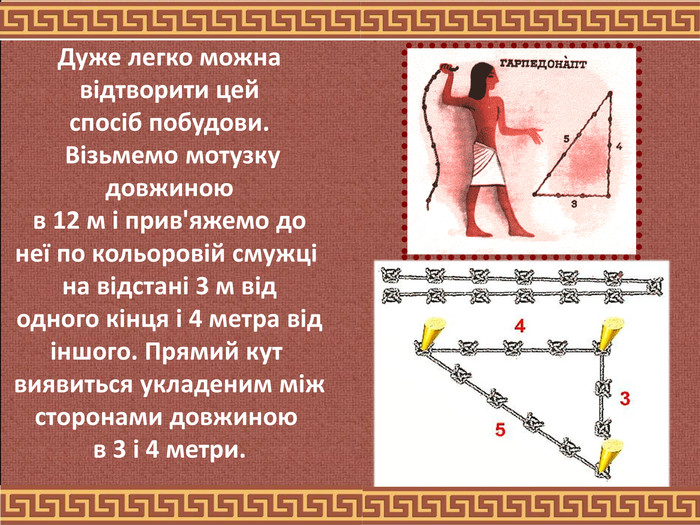
Єгипетський трикутник32+42=52 Моріц Кантор (найбільший німецький історик математики) вважає, що рівність3 ² + 4 ² = 5 ² було відомо вже єгиптянам ще близько 2300 р. до н. е.., за часів царя Аменемхета I (згідно папірусу 6619 Берлінського музею). На думку Кантора, гарпедонапти, або «натягувачі мотузок», будували прямі кути за допомогою прямокутних трикутників зі сторонами 3, 4 і 5.


про публікацію авторської розробки
Додати розробку