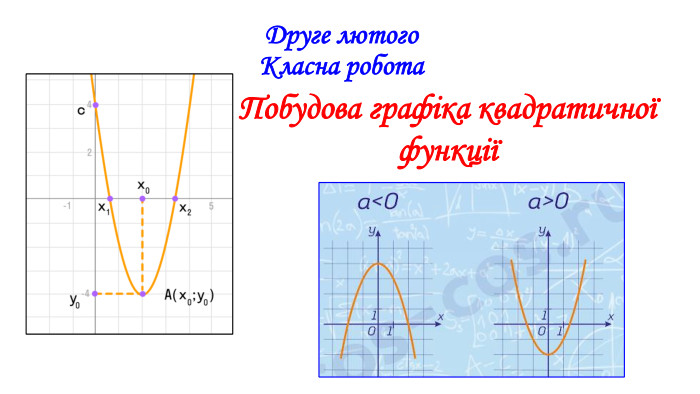
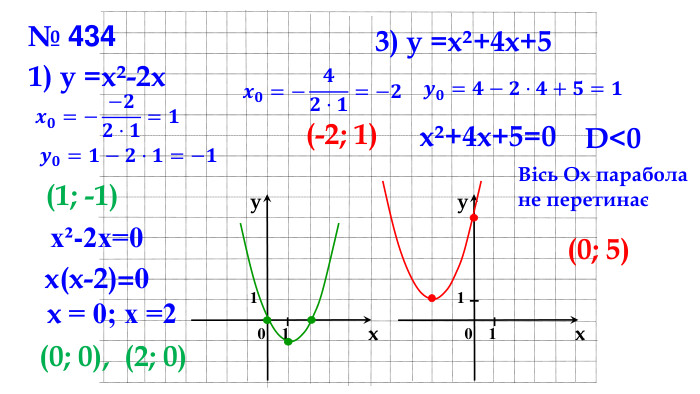
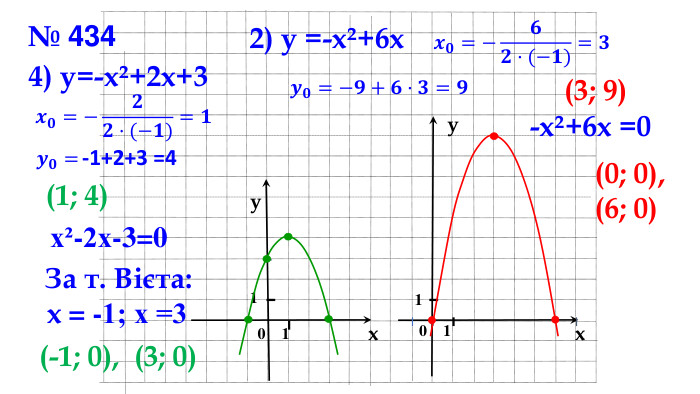
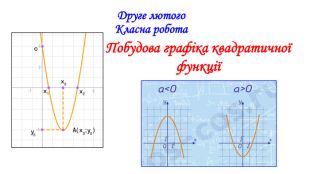
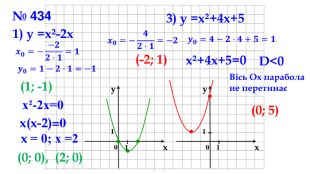
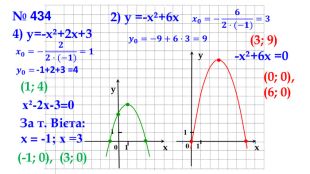
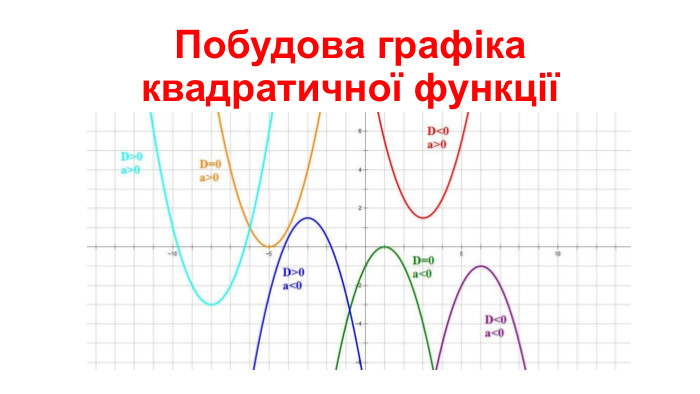
Презентація "Побудова графіка квадратичної функції"
Про матеріал
Презентація призначена для проведення уроку алгебри в дистанційному форматі у 9 класі за підручником О. С. Істер (2017). Містить елементи анімації, що дуже зручно при проведені уроку вчителем і спілкуванні з дітьми. Матеріал підібраний у логічній послідовності. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 9 клас (Істер О. С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку




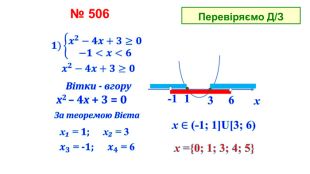
![№ 506 Перевіряємо Д/З𝟏)𝒙𝟐−𝟒𝒙+𝟑≥𝟎−𝟏<𝒙<𝟔 Вітки - вгоруx₁ = 1; x₂ = 3х. За теоремою Вієтаx2 – 4х + 3 = 0 𝒙𝟑 = -1; 𝒙𝟒 = 6 -1136х ={0; 1; 3; 4; 5}𝒙𝟐−𝟒𝒙+𝟑≥𝟎 х ∈ (-1; 1]U[3; 6) № 506 Перевіряємо Д/З𝟏)𝒙𝟐−𝟒𝒙+𝟑≥𝟎−𝟏<𝒙<𝟔 Вітки - вгоруx₁ = 1; x₂ = 3х. За теоремою Вієтаx2 – 4х + 3 = 0 𝒙𝟑 = -1; 𝒙𝟒 = 6 -1136х ={0; 1; 3; 4; 5}𝒙𝟐−𝟒𝒙+𝟑≥𝟎 х ∈ (-1; 1]U[3; 6)](/uploads/files/1973876/393252/450082_images/5.jpg)
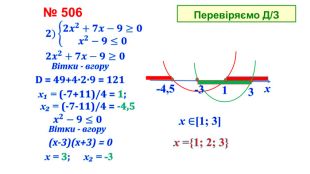
![№ 506 Перевіряємо Д/Зx₁ = (-7+11)/4 = 1; x₂ = (-7-11)/4 = -4,5хx = 3; x₂ = -3-4,5-31х ={1; 2; 3}Вітки - вгору(х-3)(х+3) = 0𝟐)𝟐𝒙𝟐+𝟕𝒙−𝟗≥𝟎𝒙𝟐−𝟗≤𝟎 𝟐𝒙𝟐+𝟕𝒙−𝟗≥𝟎 D = 49+4·2·9 = 121𝒙𝟐−𝟗≤𝟎 Вітки - вгору3х ∈[1; 3] № 506 Перевіряємо Д/Зx₁ = (-7+11)/4 = 1; x₂ = (-7-11)/4 = -4,5хx = 3; x₂ = -3-4,5-31х ={1; 2; 3}Вітки - вгору(х-3)(х+3) = 0𝟐)𝟐𝒙𝟐+𝟕𝒙−𝟗≥𝟎𝒙𝟐−𝟗≤𝟎 𝟐𝒙𝟐+𝟕𝒙−𝟗≥𝟎 D = 49+4·2·9 = 121𝒙𝟐−𝟗≤𝟎 Вітки - вгору3х ∈[1; 3]](/uploads/files/1973876/393252/450082_images/6.jpg)