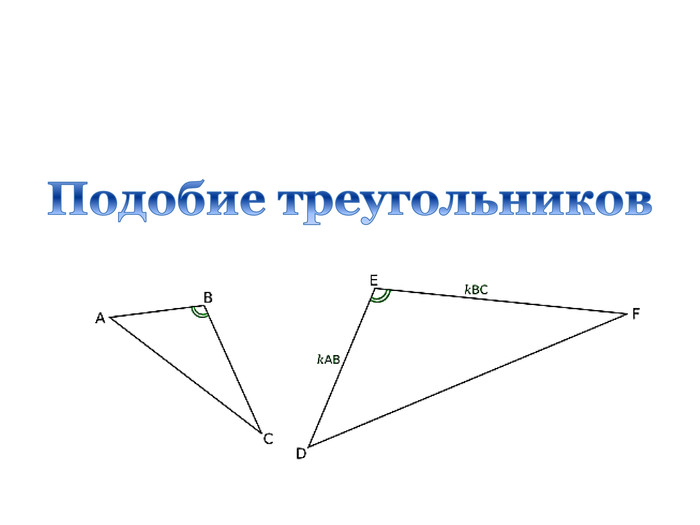
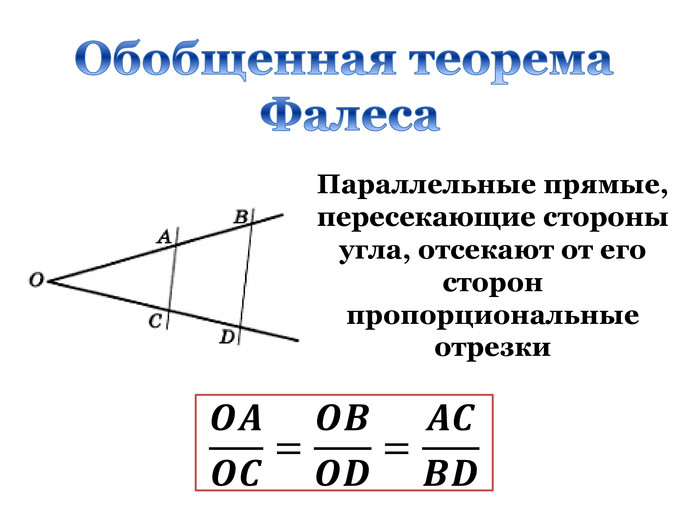
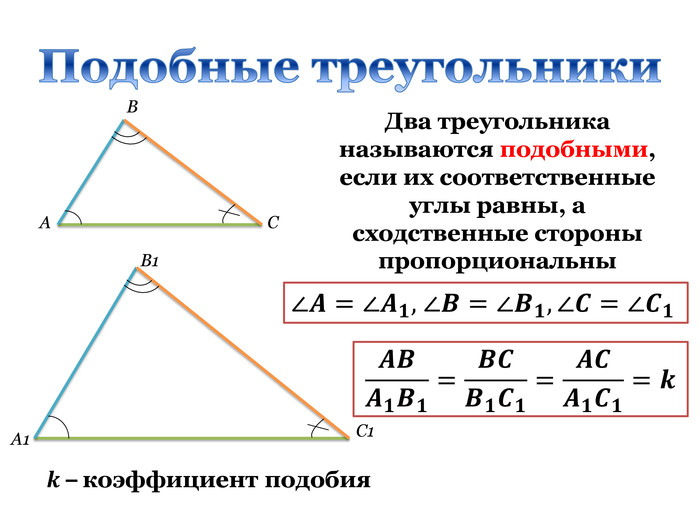
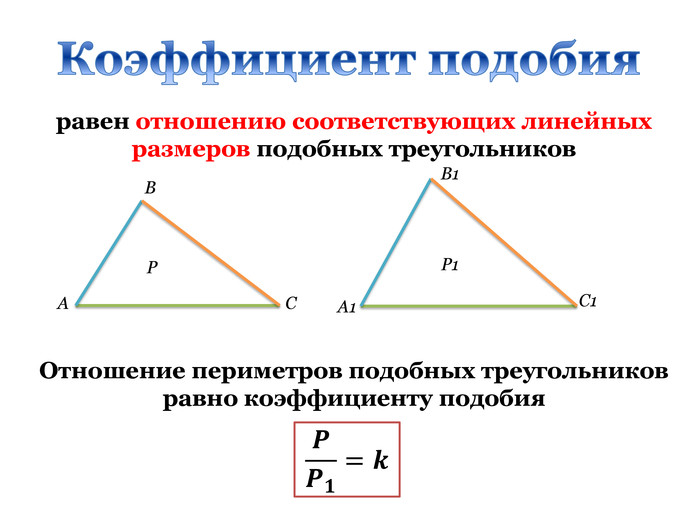
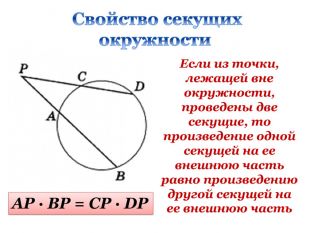
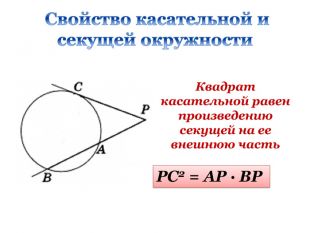
Презентація "Подібність трикутників. Узагальнення та систематизація"
Про матеріал
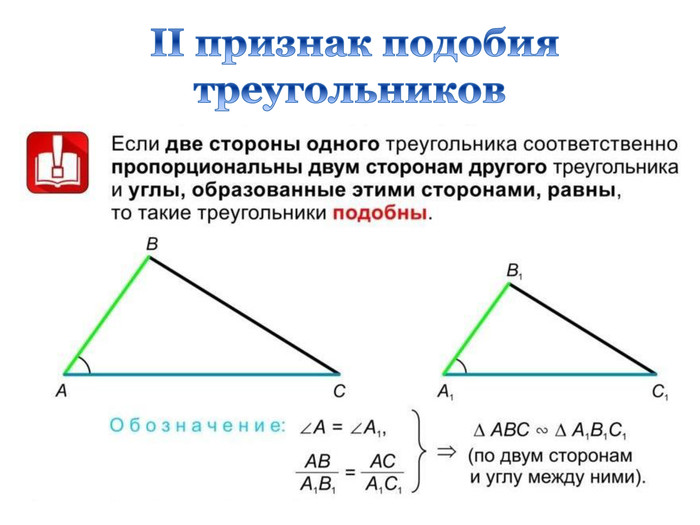
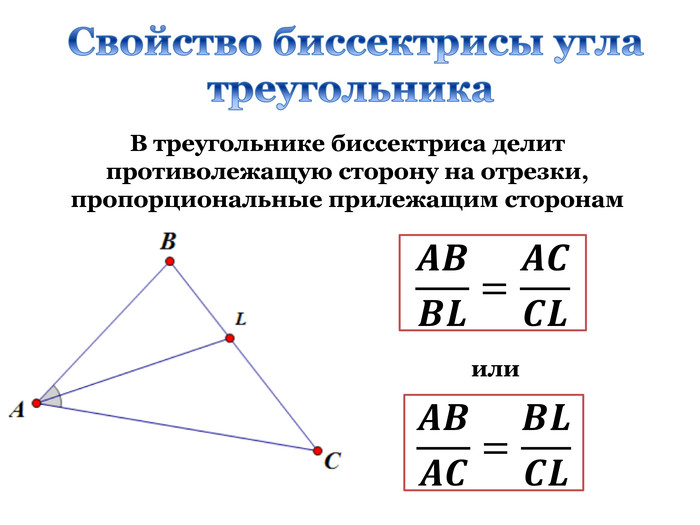
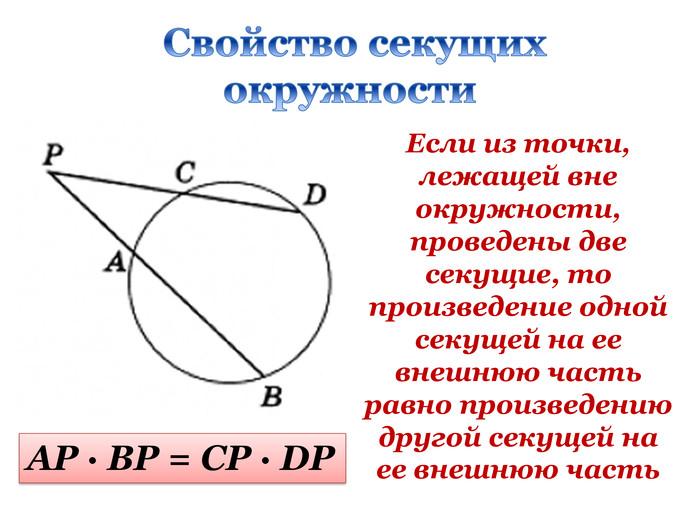
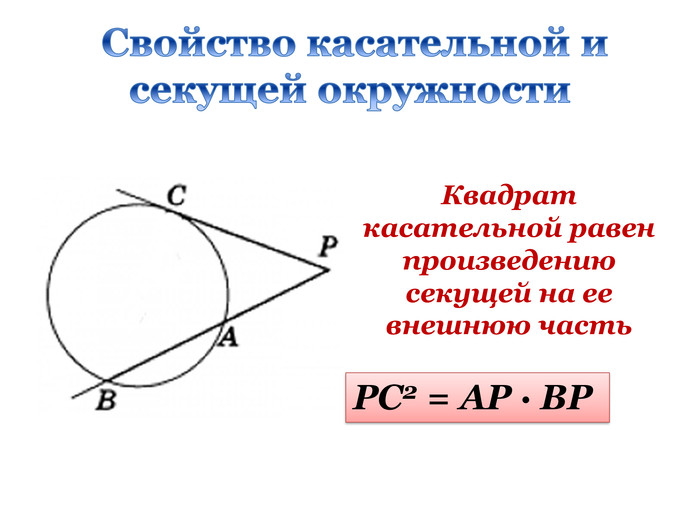
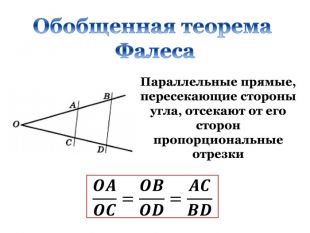
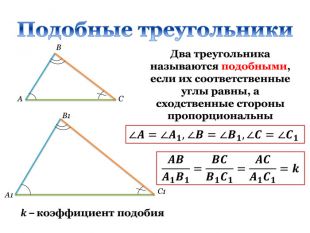
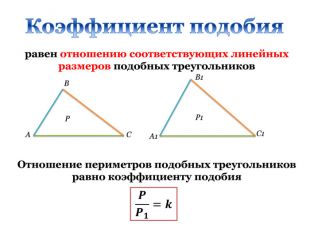
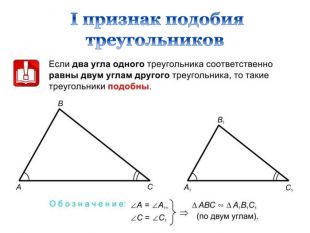
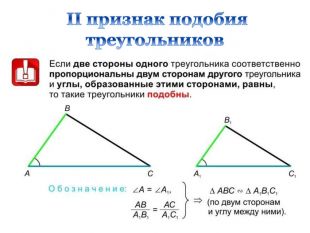
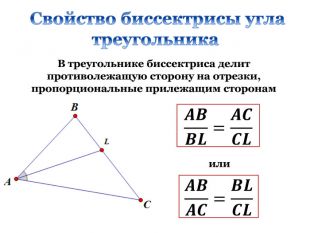
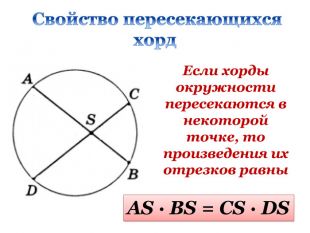
Дана презентація є допоміжним матеріалом до уроку узагальнення та систематизації знань учнів 8 класу за темою "Подібність трикутників". Вона містить усі необхідні теоретичні матеріали по даній теми та добірку різнорівневих задач, які допоможуть підготувати учнів до тематичного оцінювання за цією темою. Даний урок опробований на 8 класі з поглибленим вивченням математики комунального закладу освіти "Спеціалізована школа № 129 фізико-математичного профілю" Дніпровської ради.
Даний матеріал може бути використаний й вчителями, які викладають математику за рівнем "Стандарт" Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку