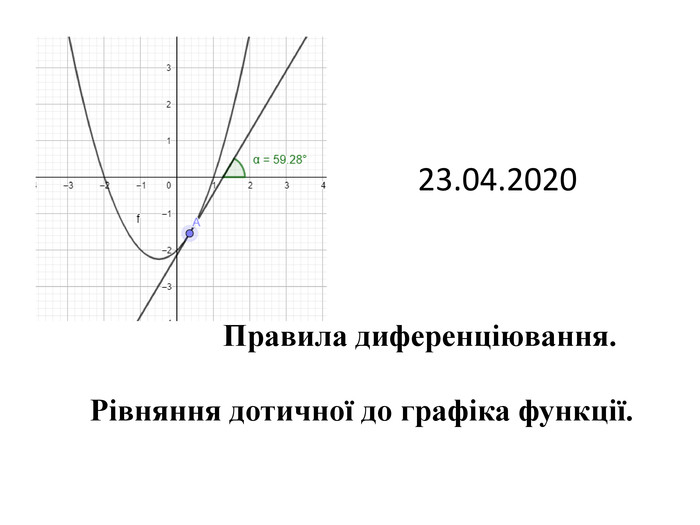
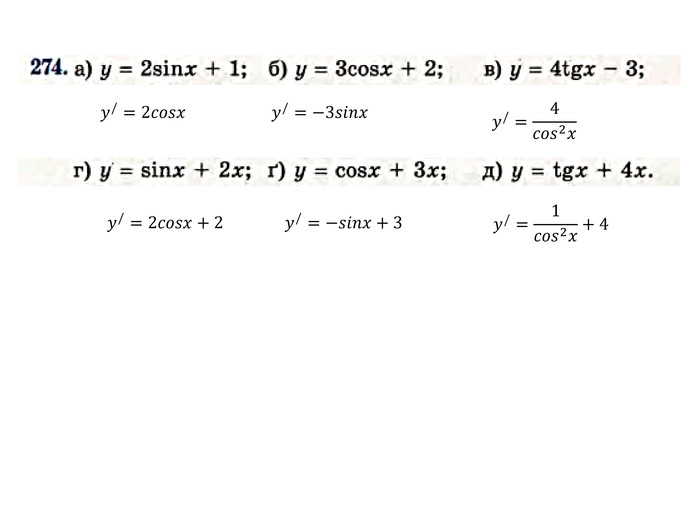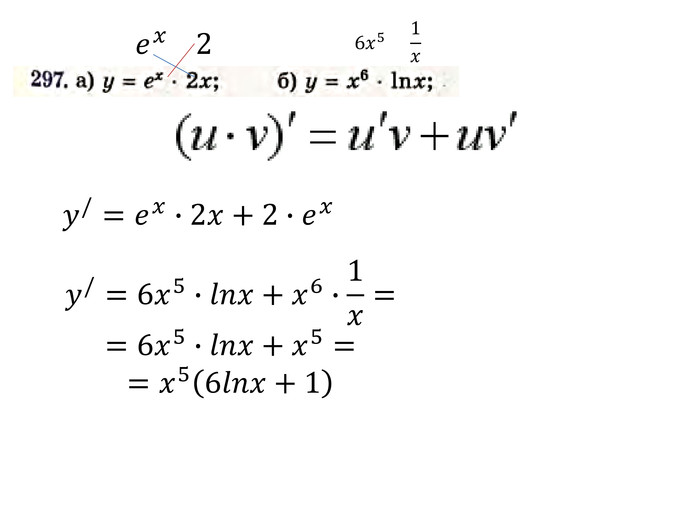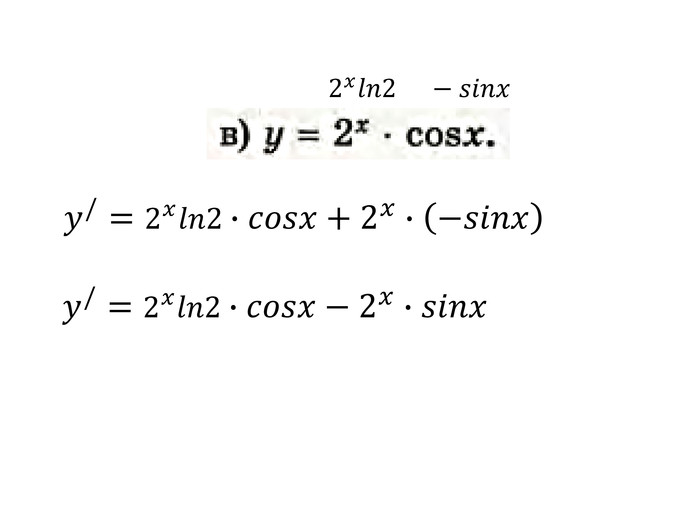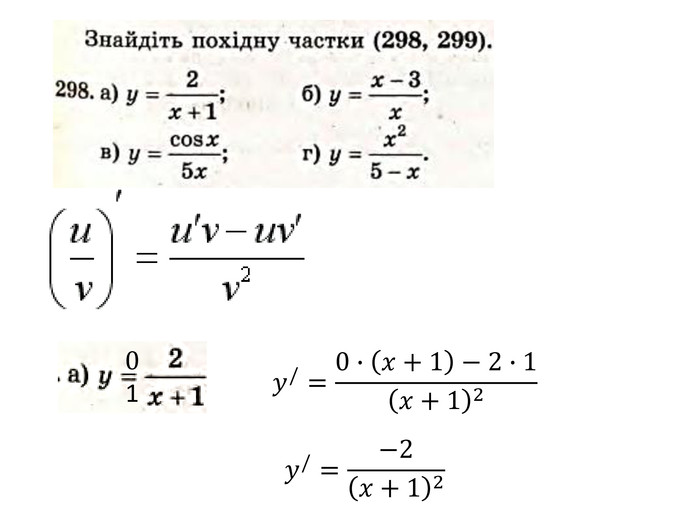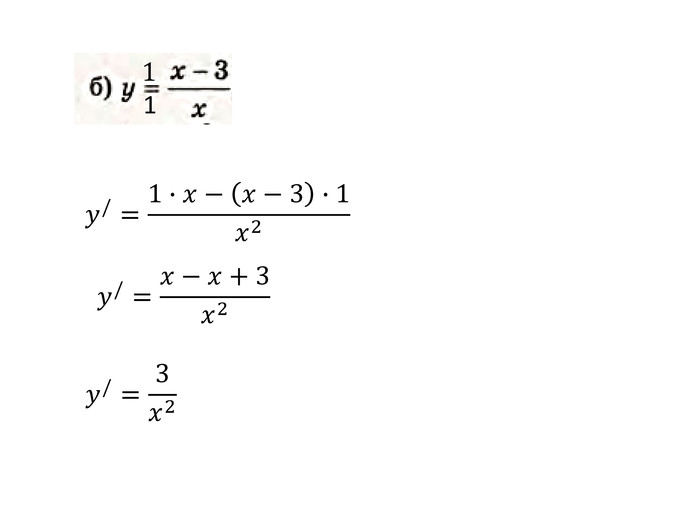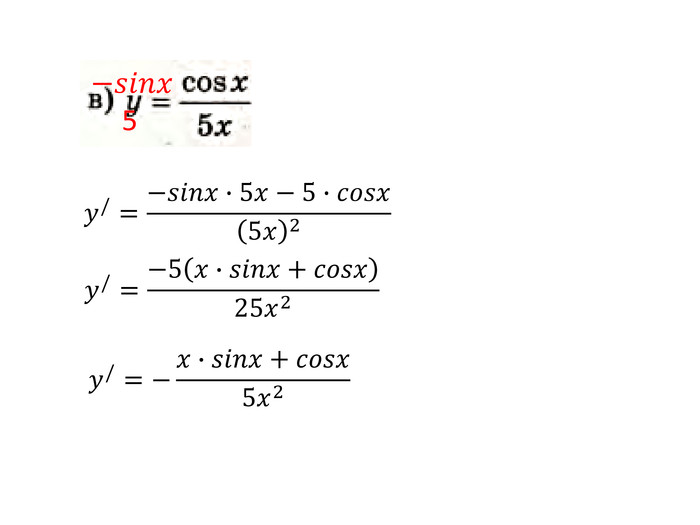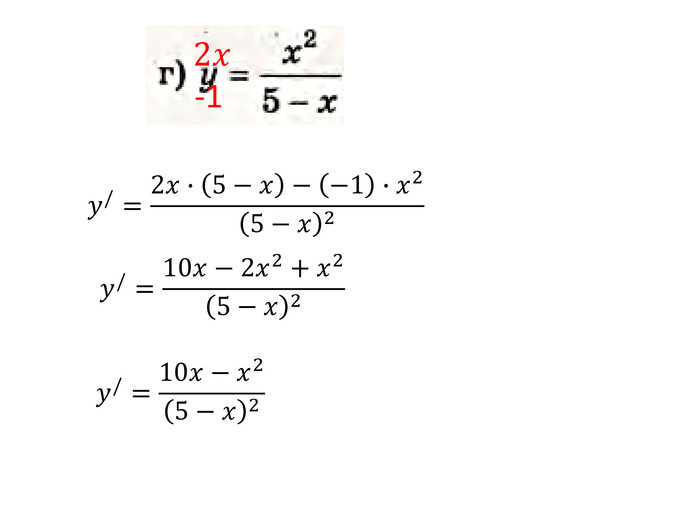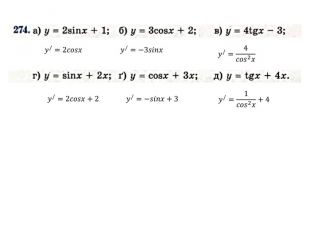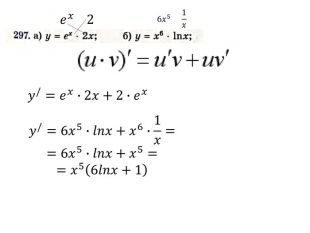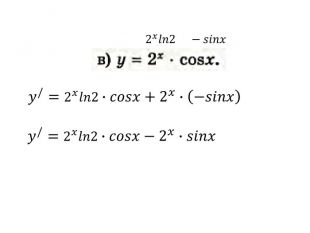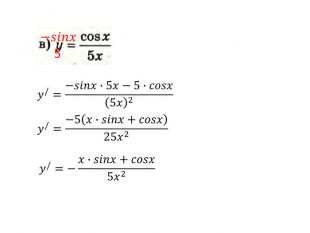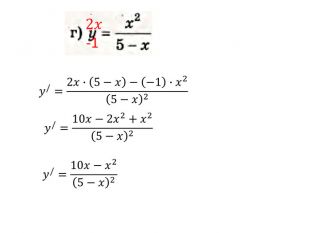Презентація "Похідна від частки та добутку. Рівняння дотичної до графіка функції"
Про матеріал
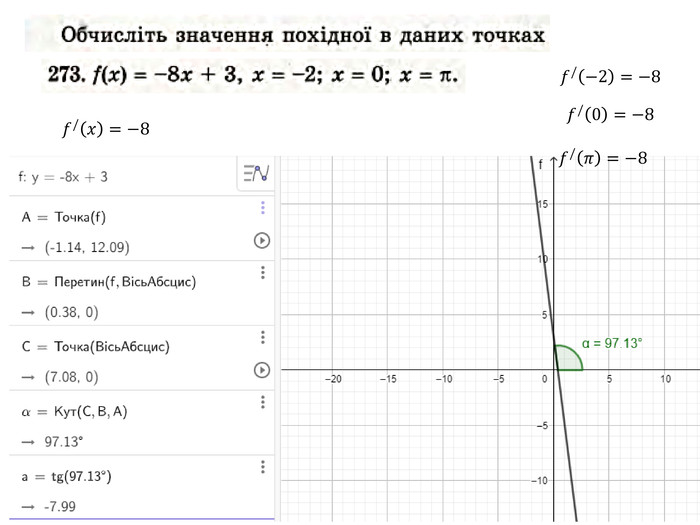
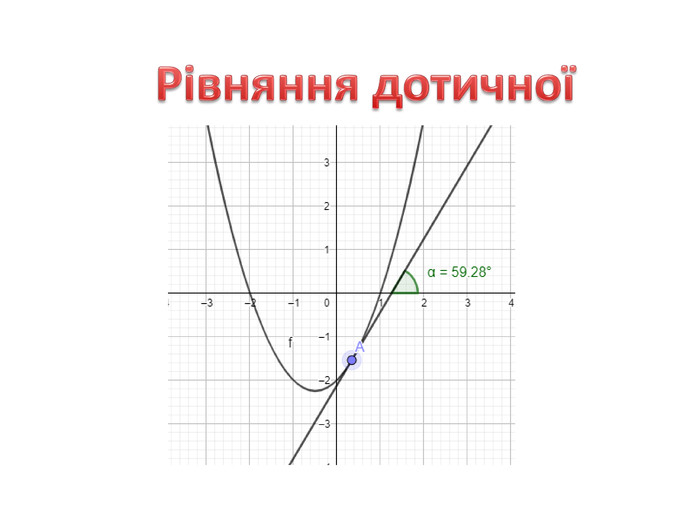
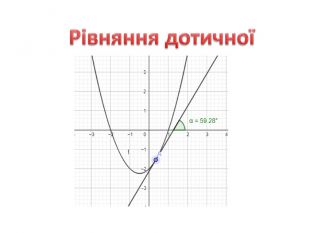
Презентація "Похідна від частки та добутку. Рівняння дотичної до графіка функції" містить завдання підручника Бевз Г.П. Математика 11 клас, 2011 рік. Презентація містить детальний розгляд прикладів на знаходження похідної від добутку та частки, а також знаходження рівняння дотичної до графіка функції в заданій точці. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку