Презентація "Показникова функція, показникові рівняння і нерівності"
Про матеріал
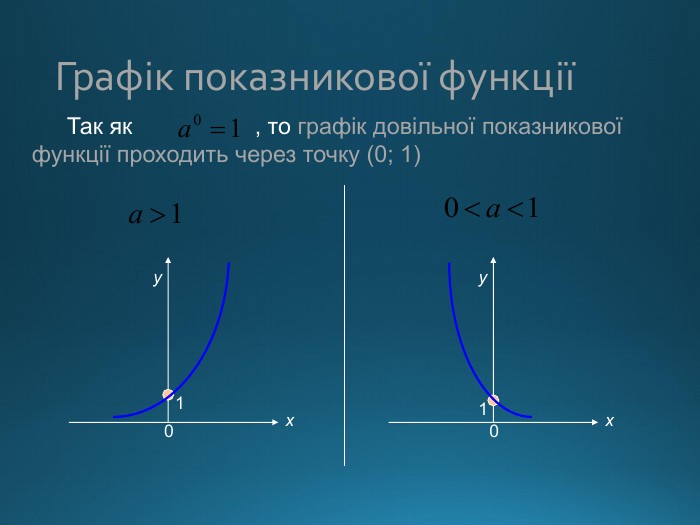
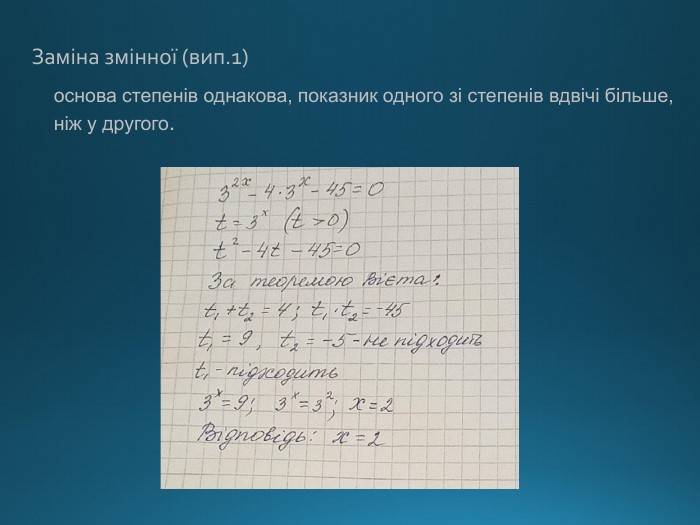
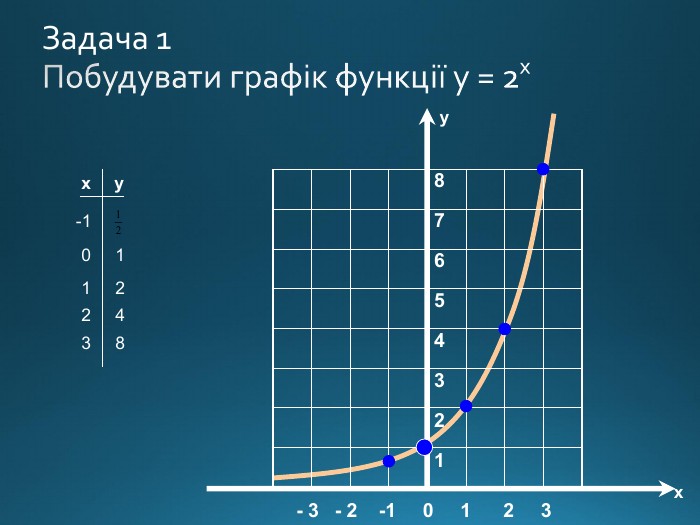
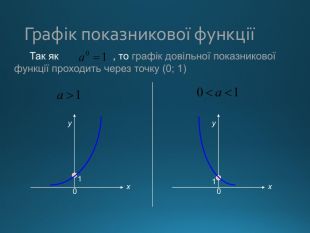
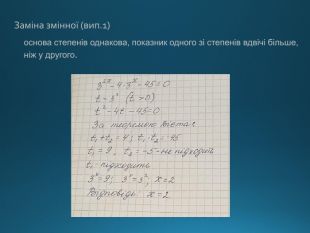
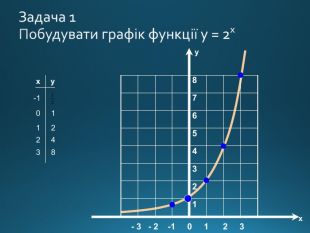
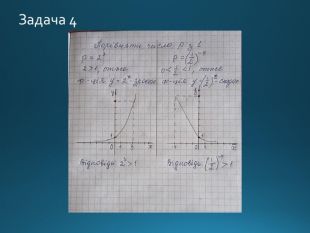
Презентація містить правила використання показникової функції для вирішення рівнянь і непівностей Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку