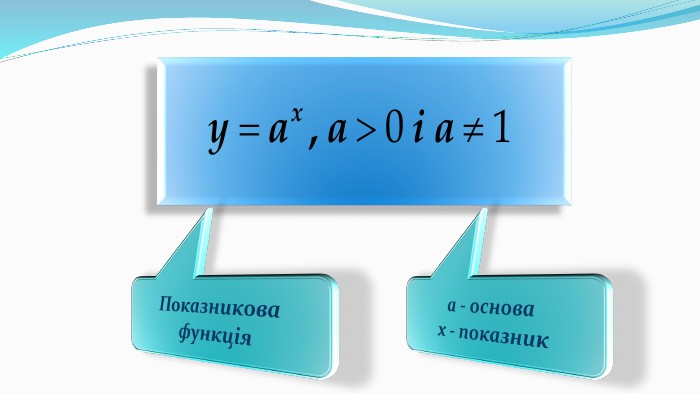
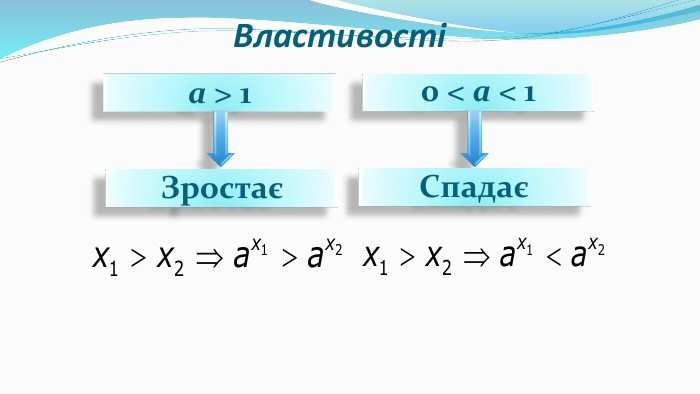
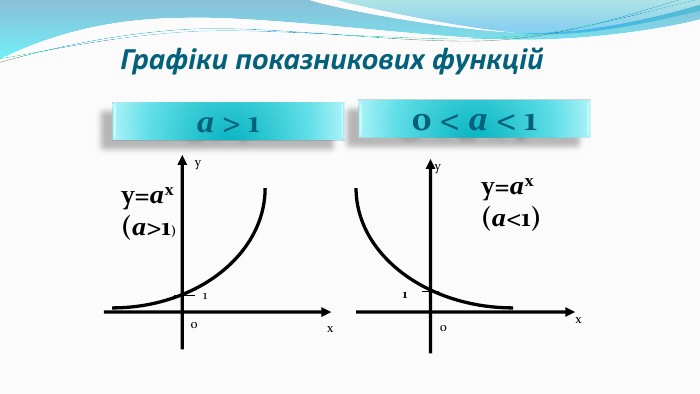
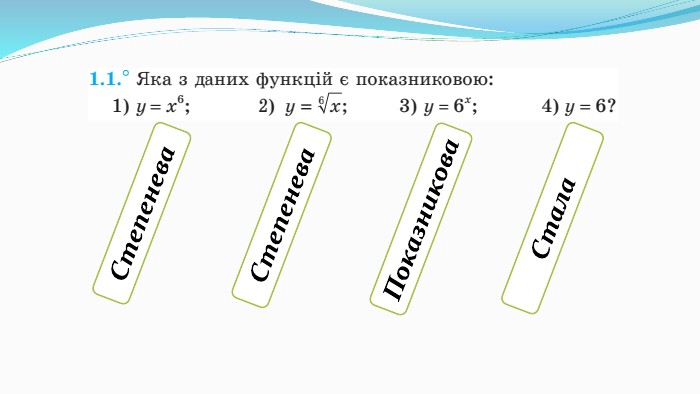
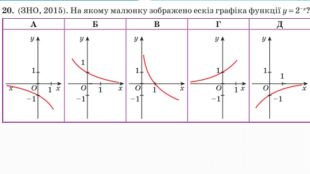
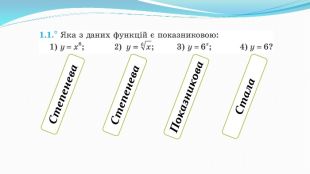
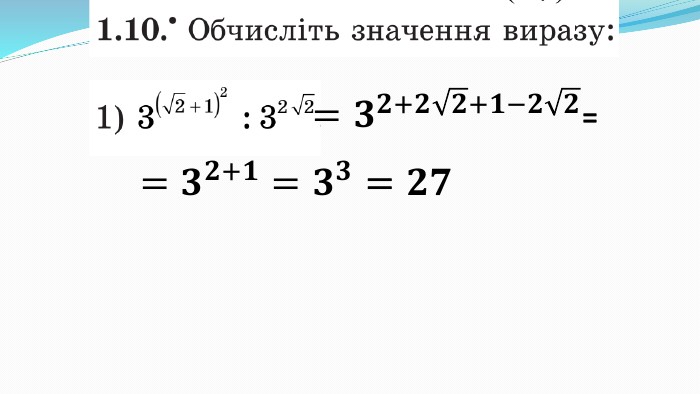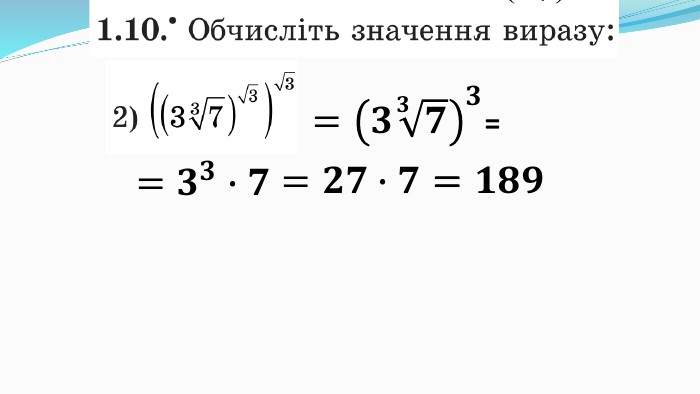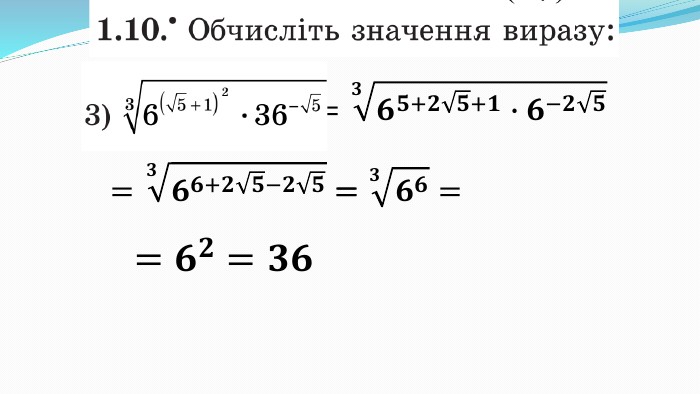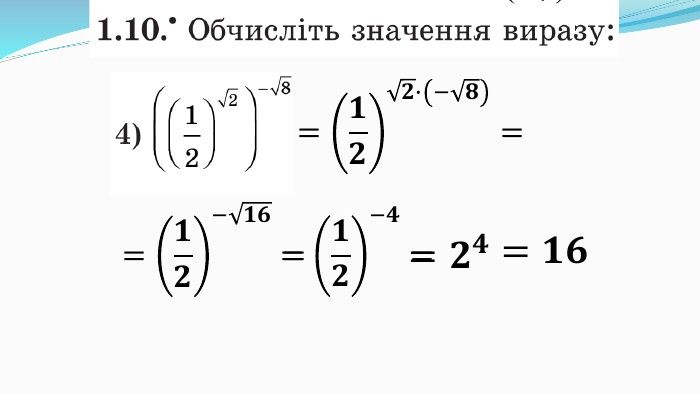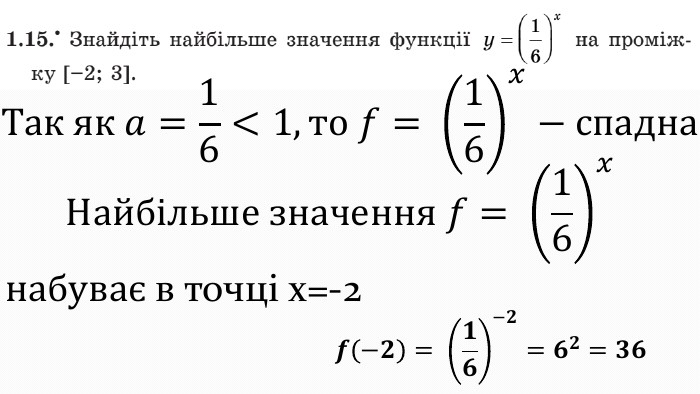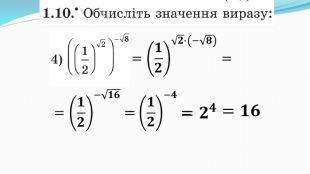Презентація "Показникова функція та її властивості"
Про матеріал
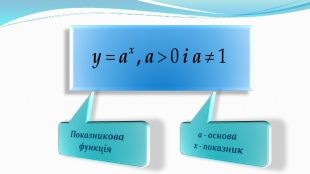
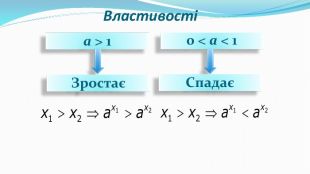
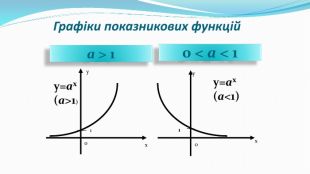
Презентація до уроку "Показникова функція та її властивості" використовується при пояснені матеріалу на уроці, демонструє застосування показникової функцій, її означення і властивості; містить вправи, що допомагають усвідомити ці властивості, а також розв'язування вправ з підручника, які націлені на формування умінь і навичок. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку