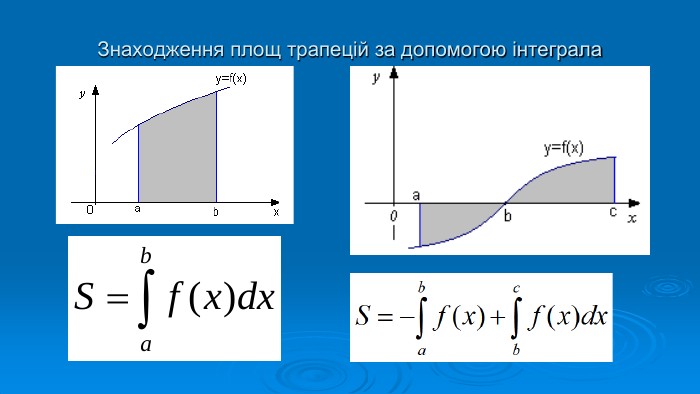
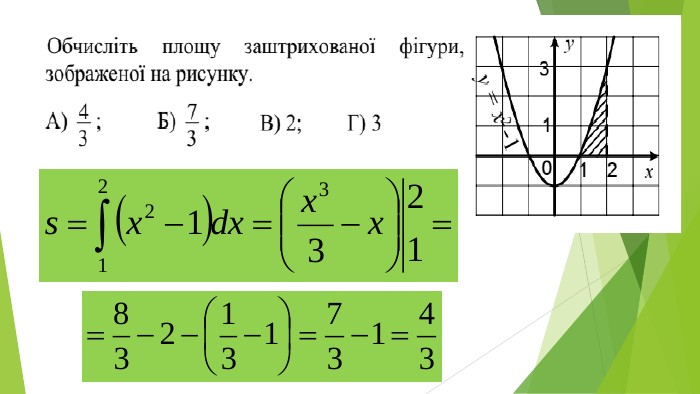
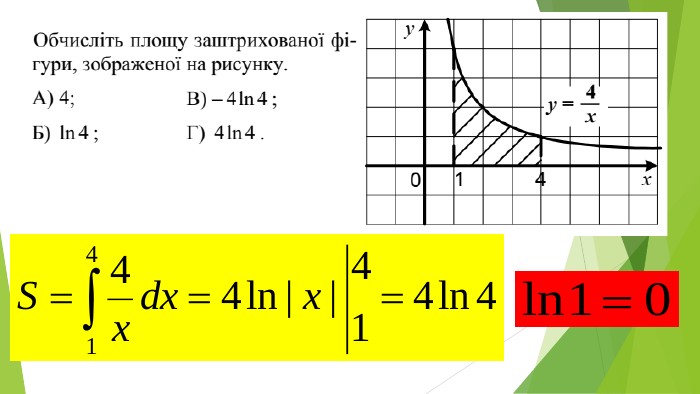
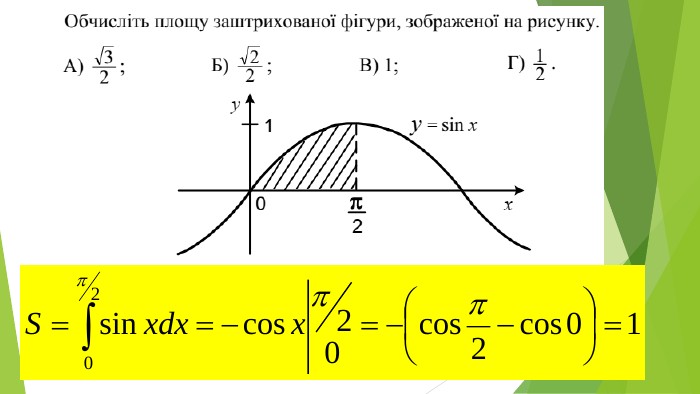
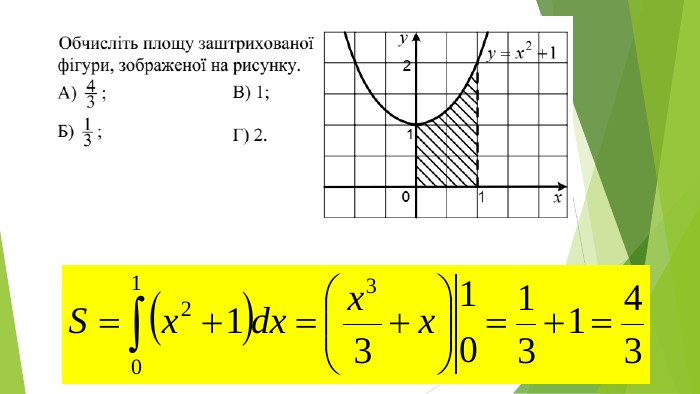
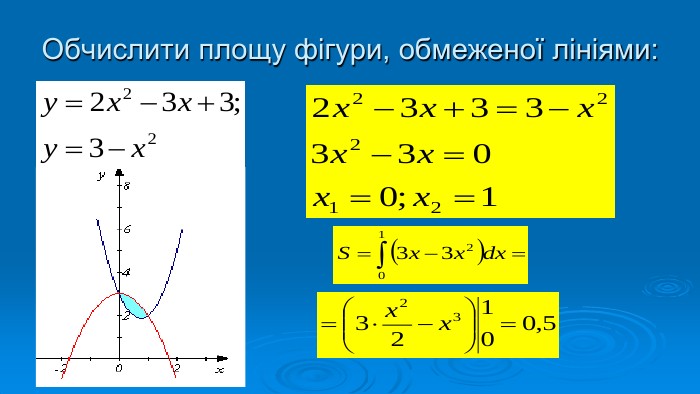
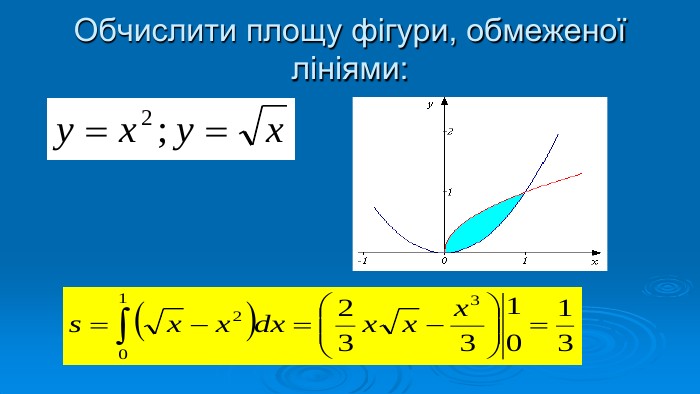
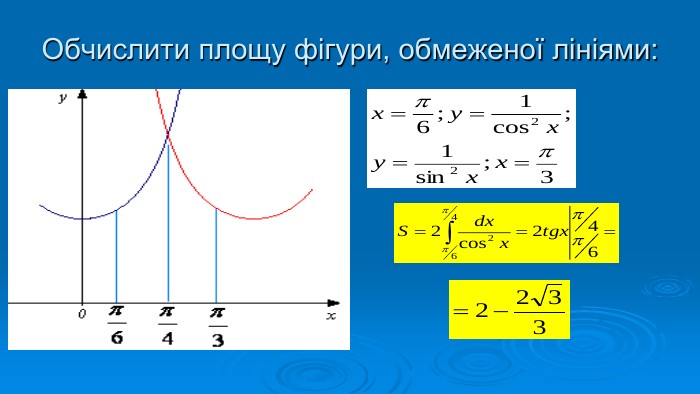
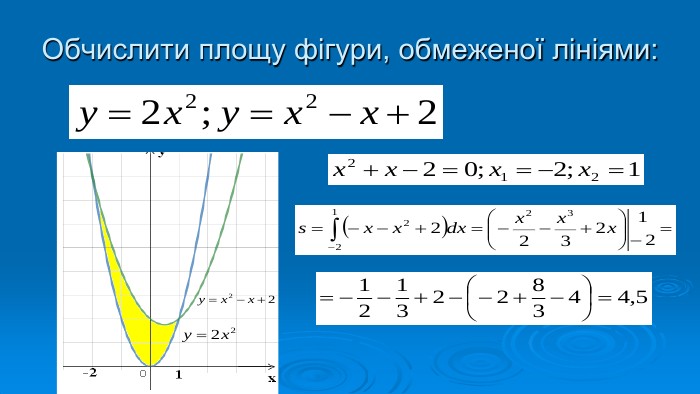
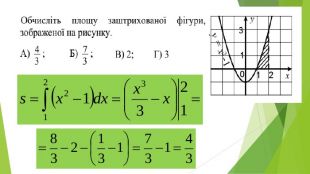
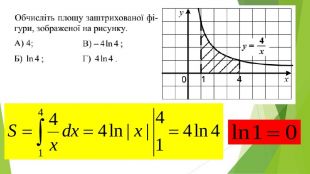
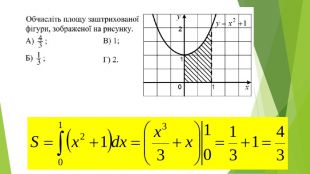
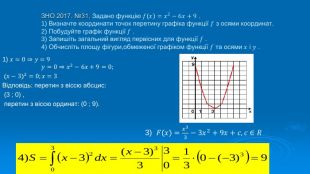
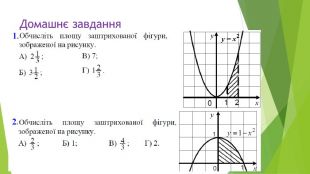
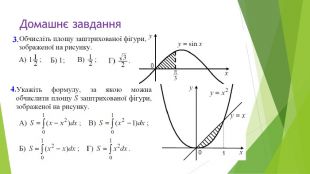
Презентація "Знаходження площ плоских фігур"
Про матеріал
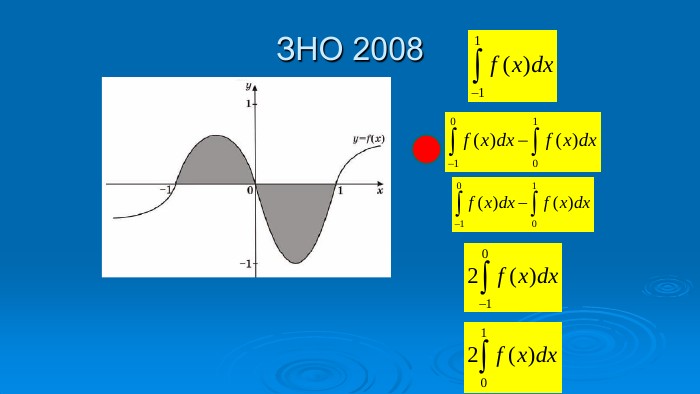
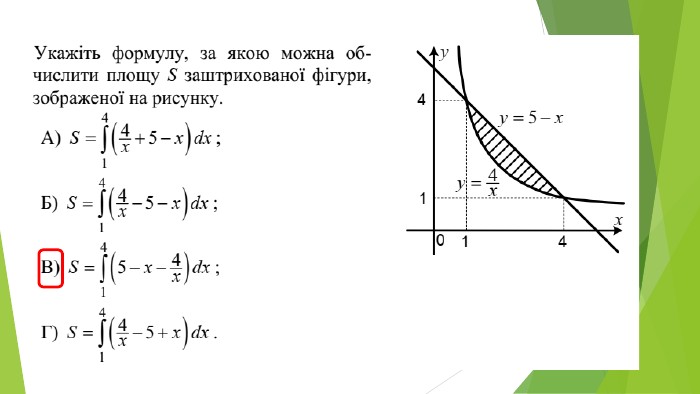
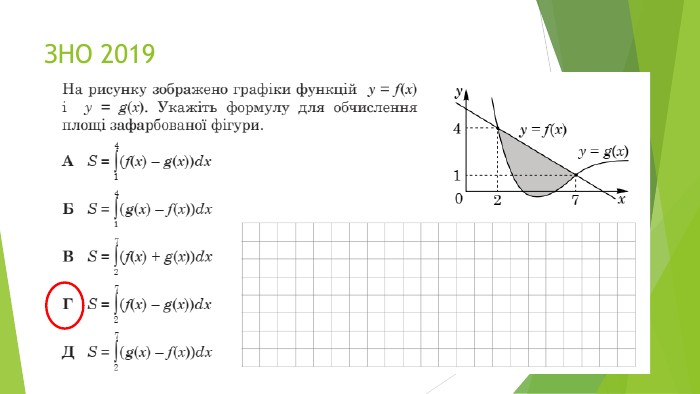
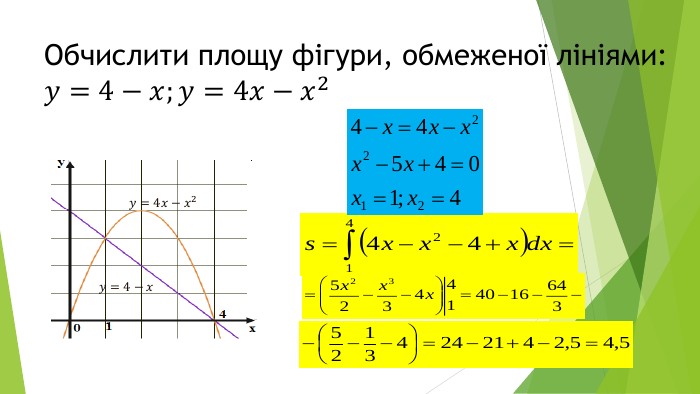
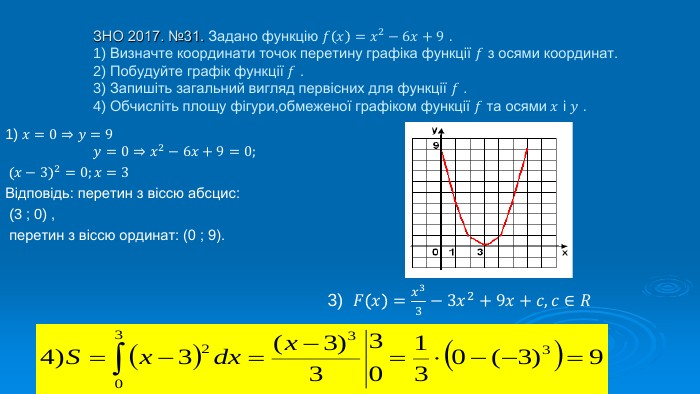
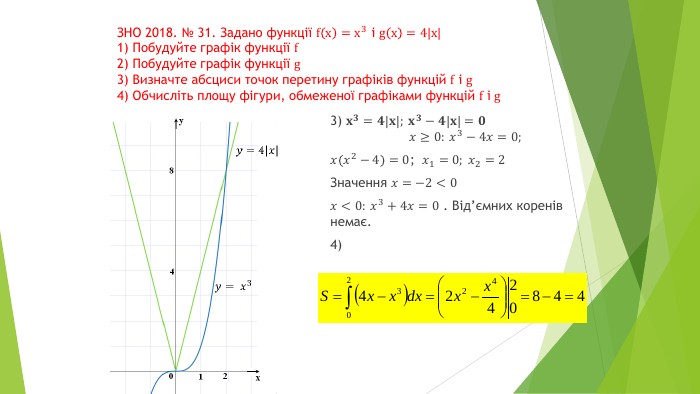
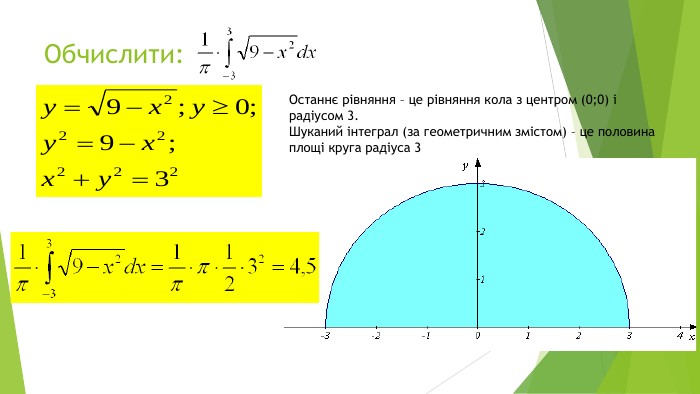
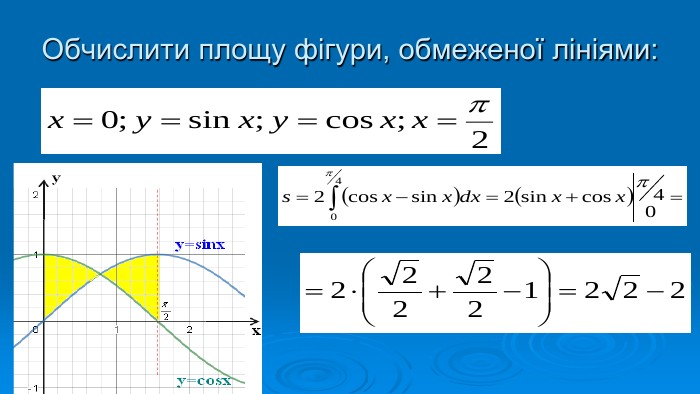
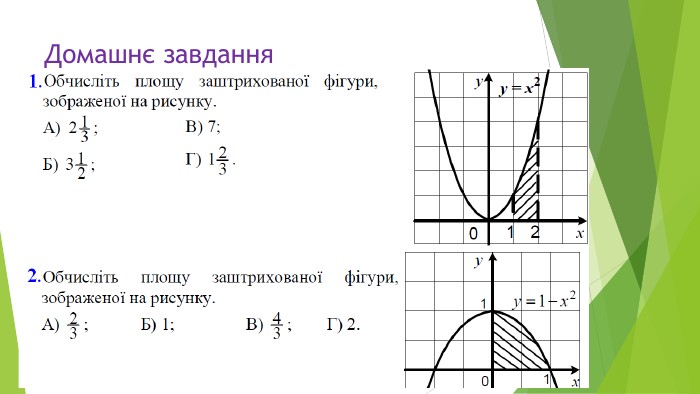
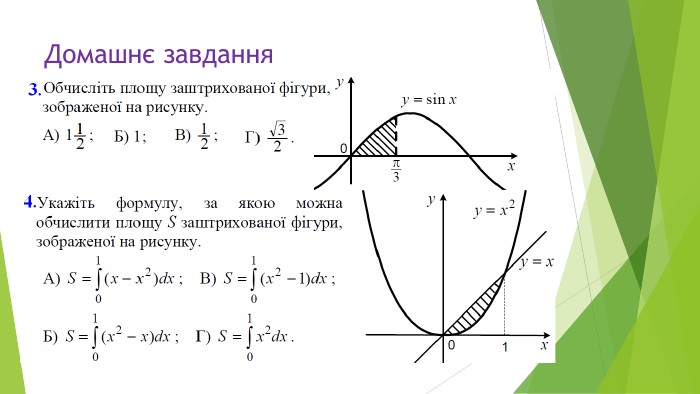
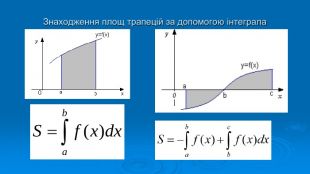
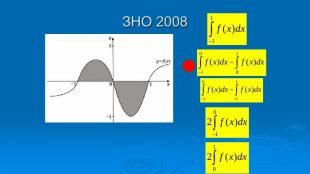
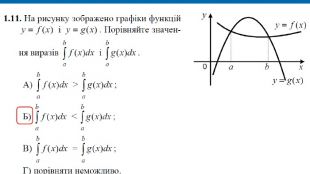
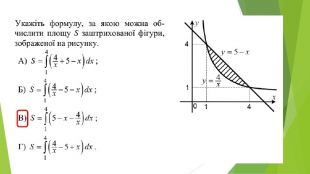
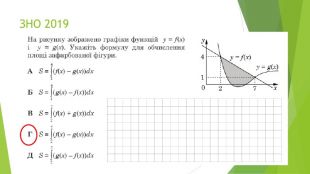
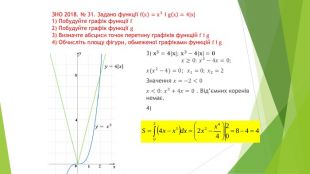
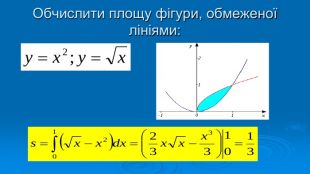
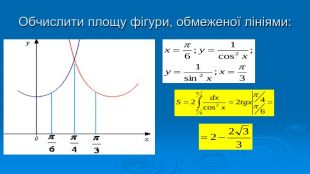
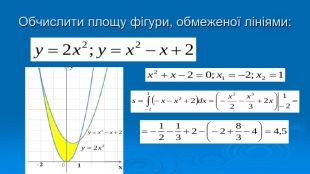
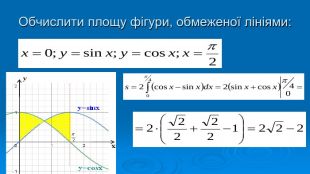
В презентації розглянуто завдання різних рівней складності щодо теми "Геометричний зміст визначеного інтегралу". В тому числі завдання ІІІ частини ЗНО Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дуже крута розробка! Дякуємо!
-
Одна із найкращих ppt на цю тему
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку