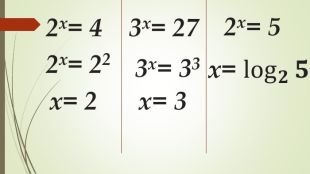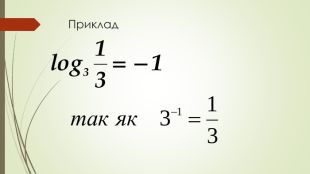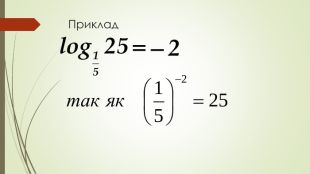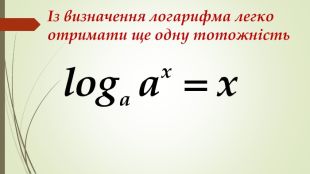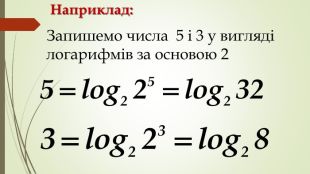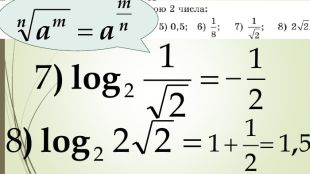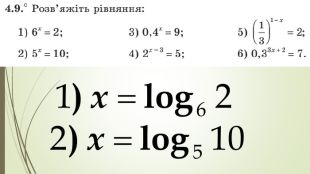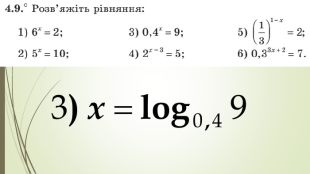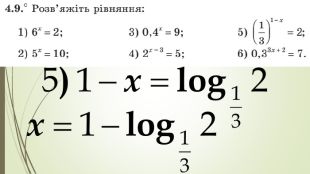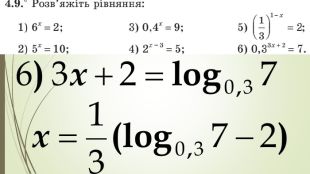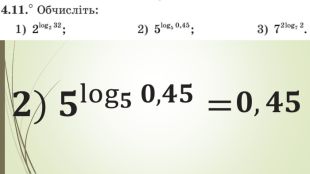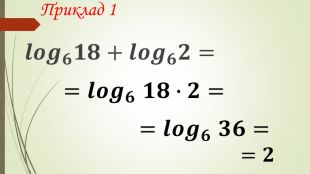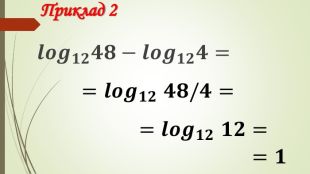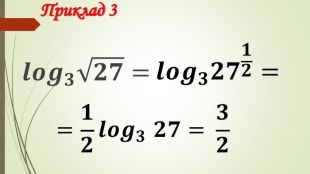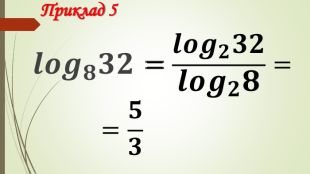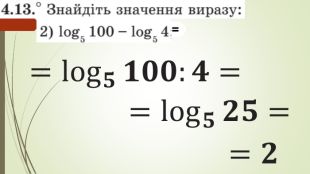Презентація "Логарифм і його властивості"
Про матеріал
Даний матеріал використовується на уроці як наочний супровод пояснення матеріалу, формування умінь і навичок учнів обчислювати логарифми. Перегляд файлу

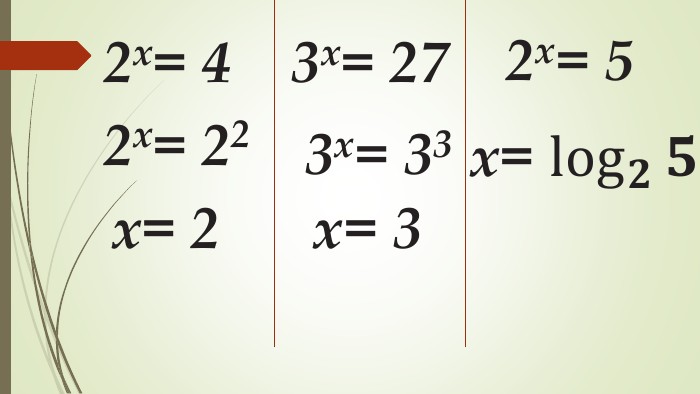



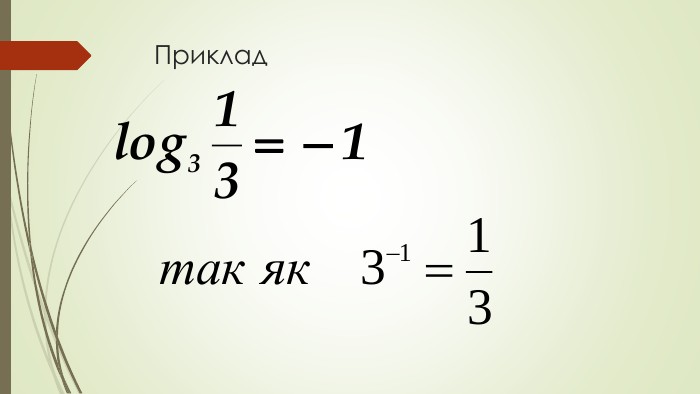
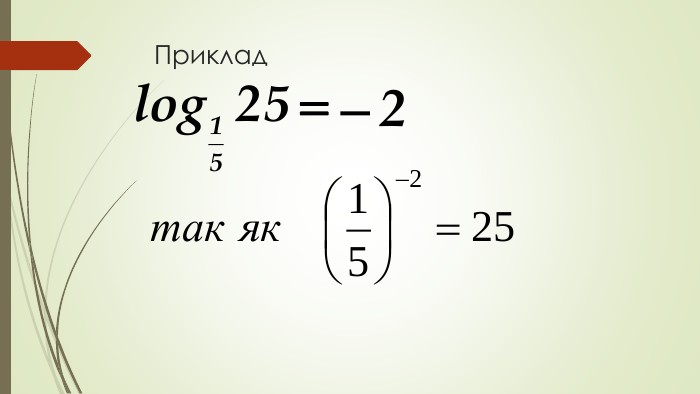


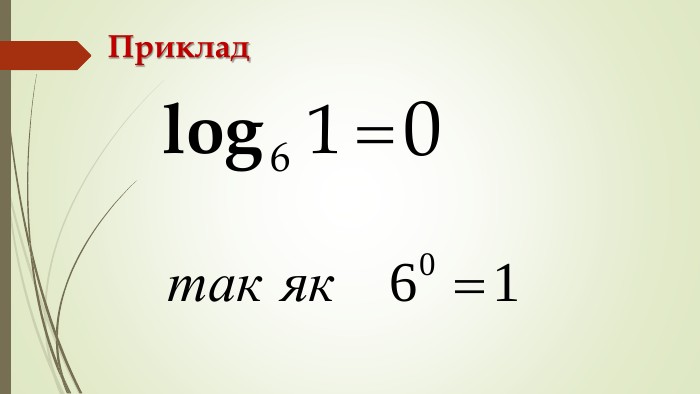






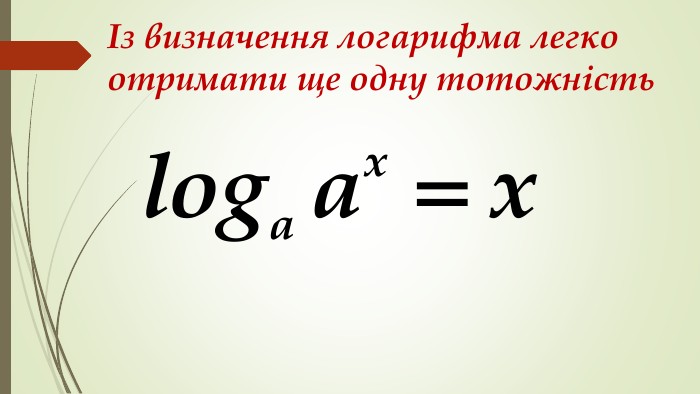



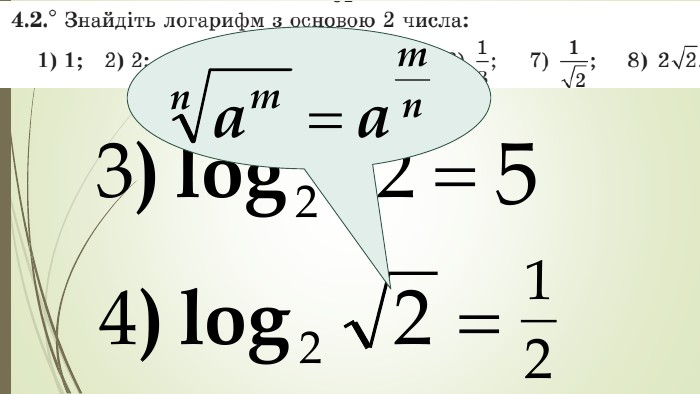

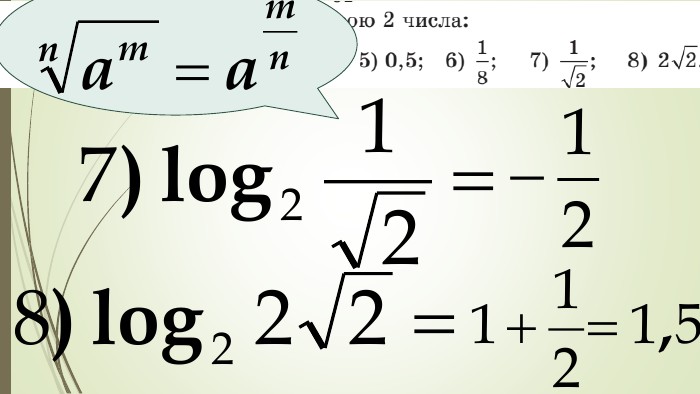
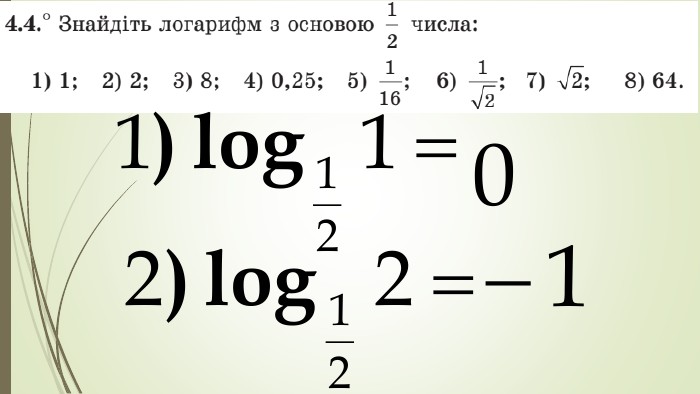


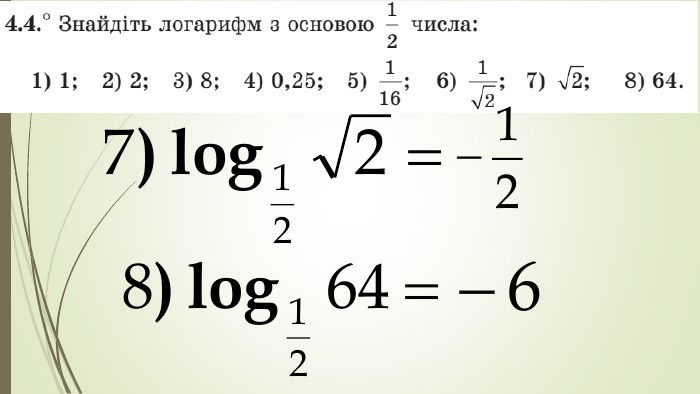


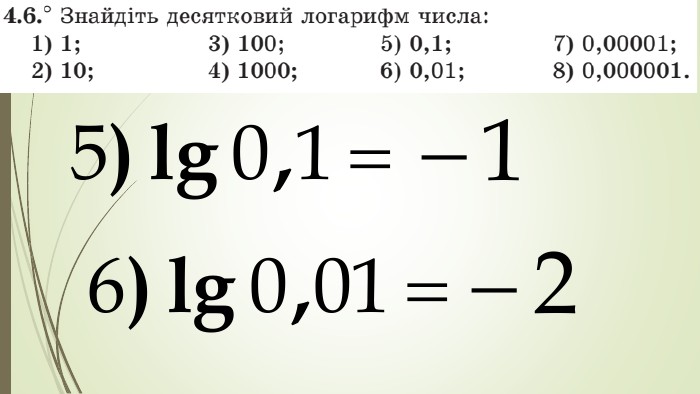

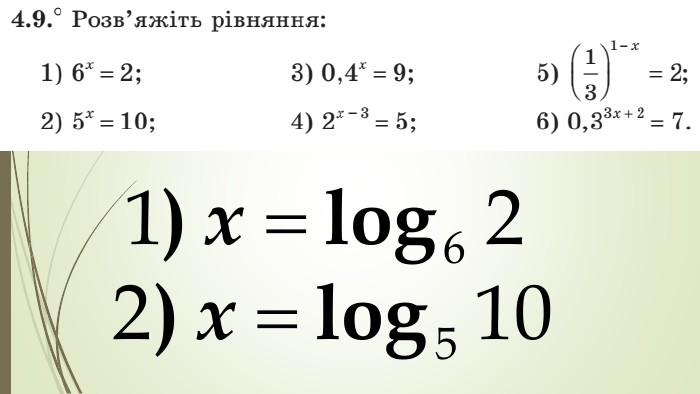

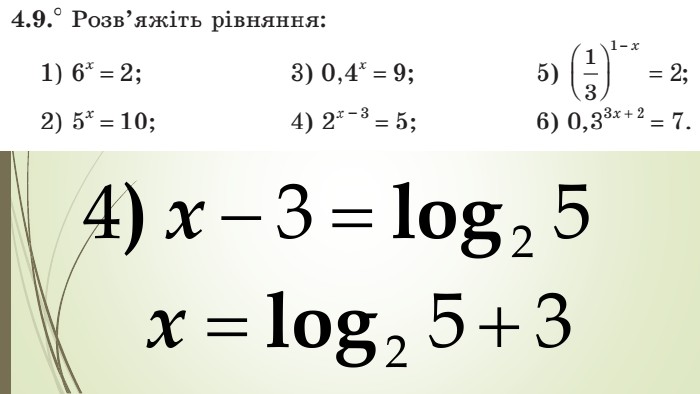

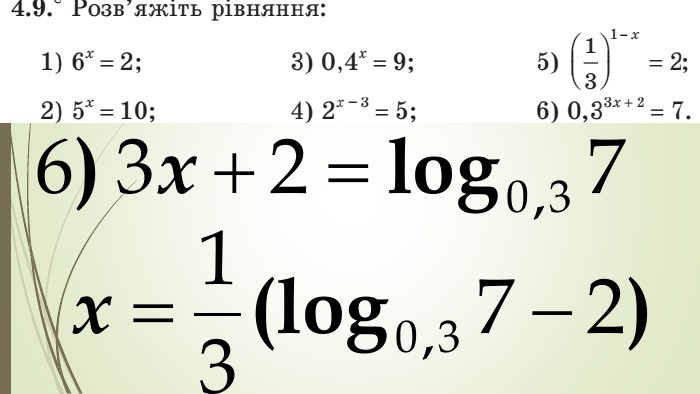
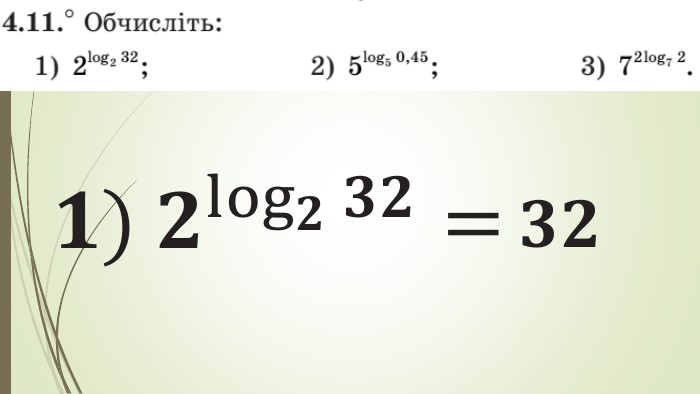
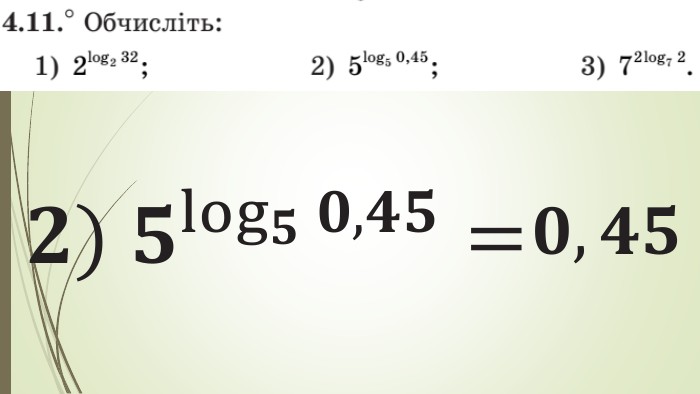
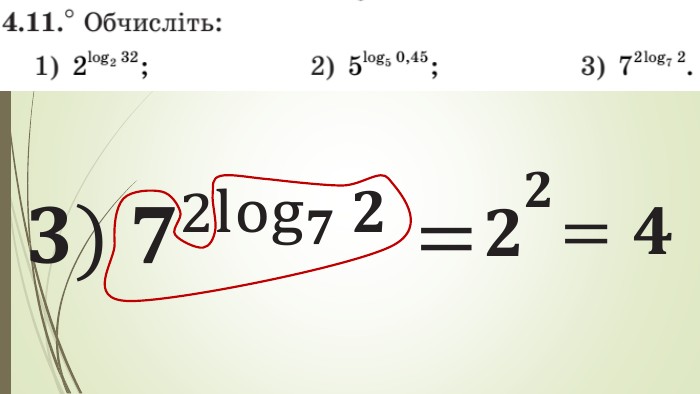



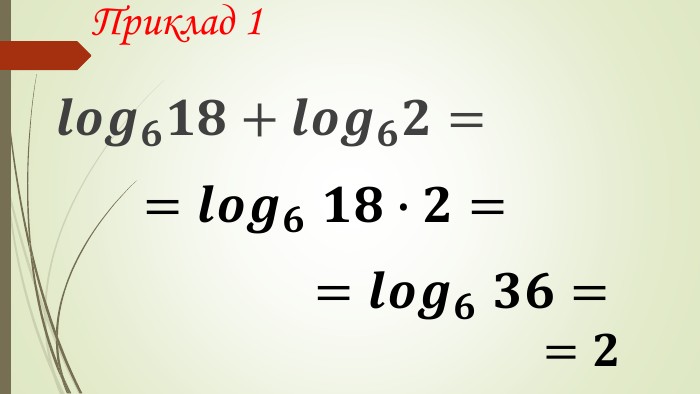

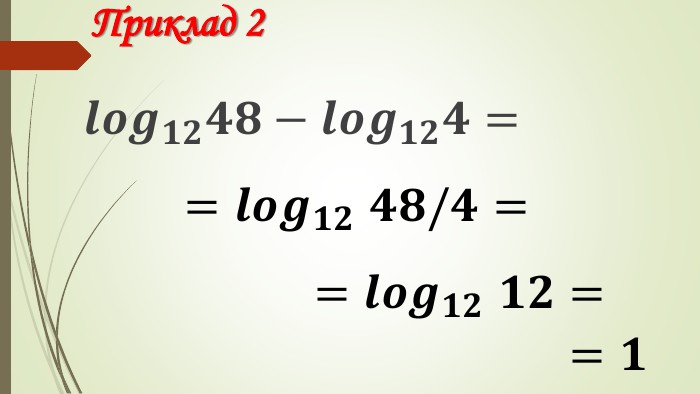

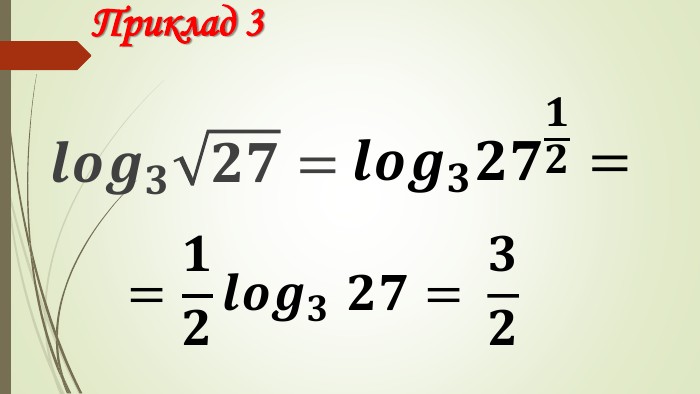

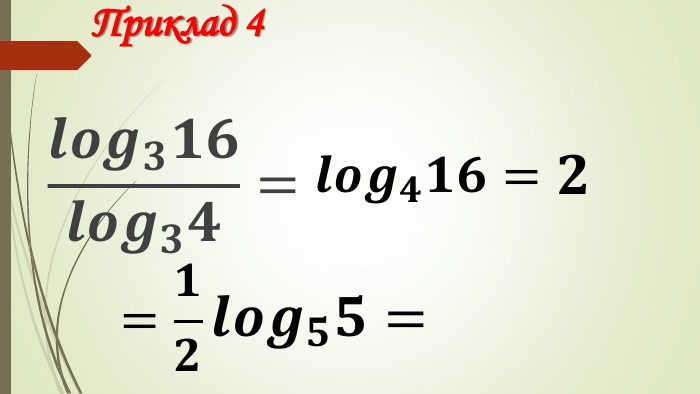


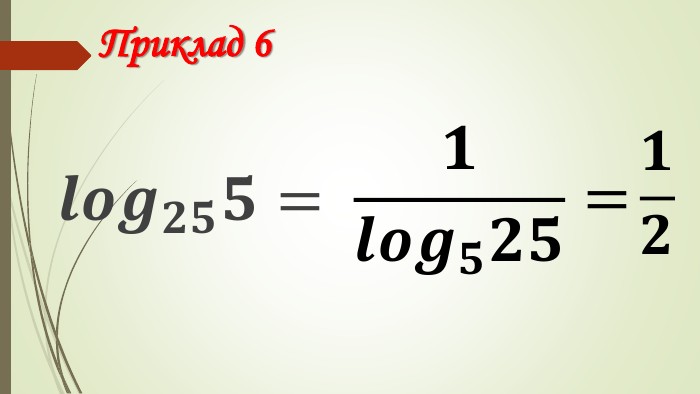

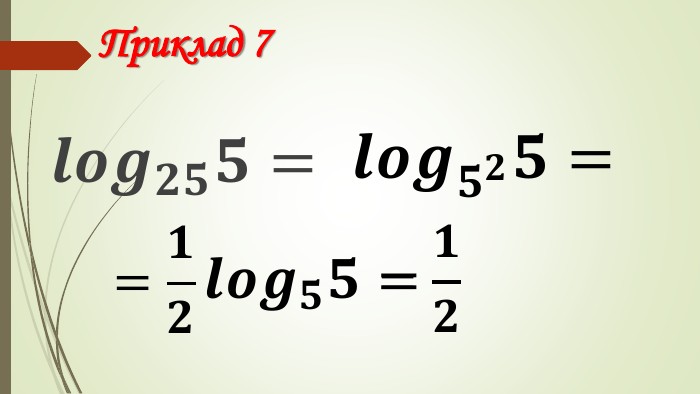

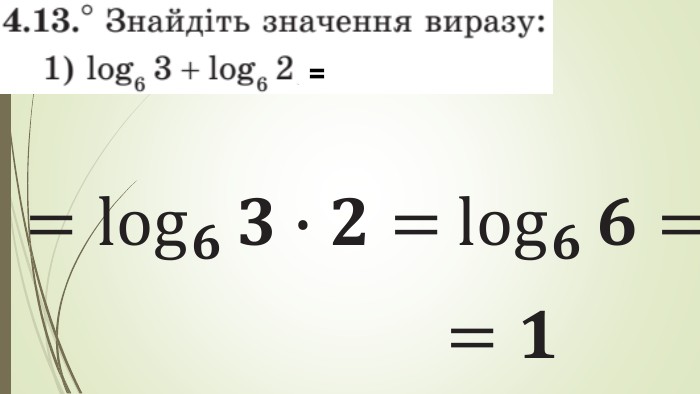
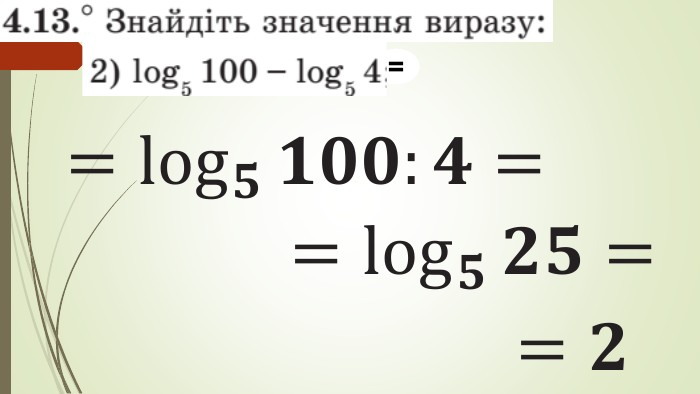

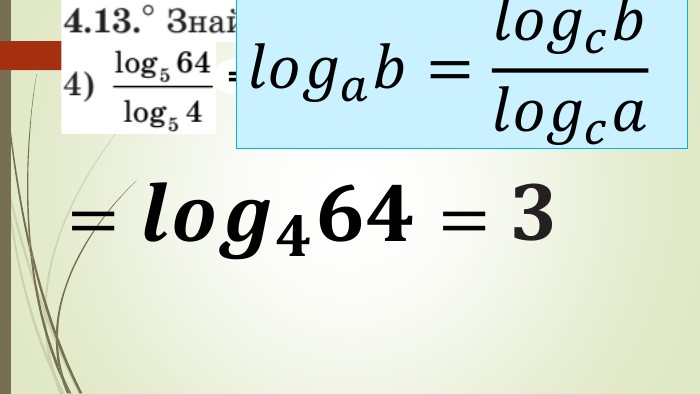
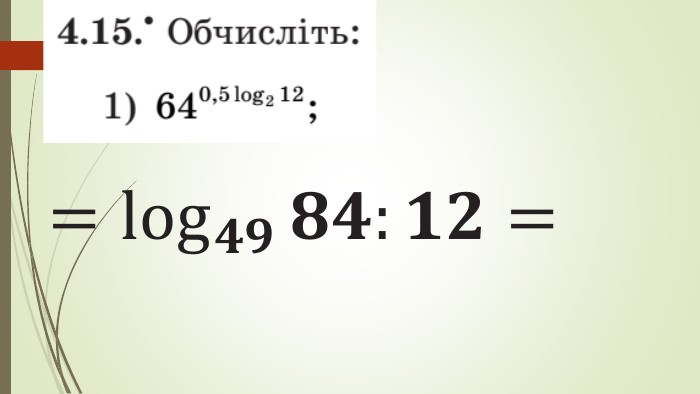

Зміст слайдів
Середня оцінка розробки
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Загальна:
5.0
Всього відгуків: 1
Оцінки та відгуки
-
 Отдатчикова Людмила Миколаївна 14.04.2022 в 07:29Чітко, послідовно, доступно.Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0
Отдатчикова Людмила Миколаївна 14.04.2022 в 07:29Чітко, послідовно, доступно.Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0
pptx
Додав(-ла)
Картавих Тетяна Олександрівна
Додано
3 січня 2022
Переглядів
1536
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
Рекомендовані матеріали
Схожі матеріали