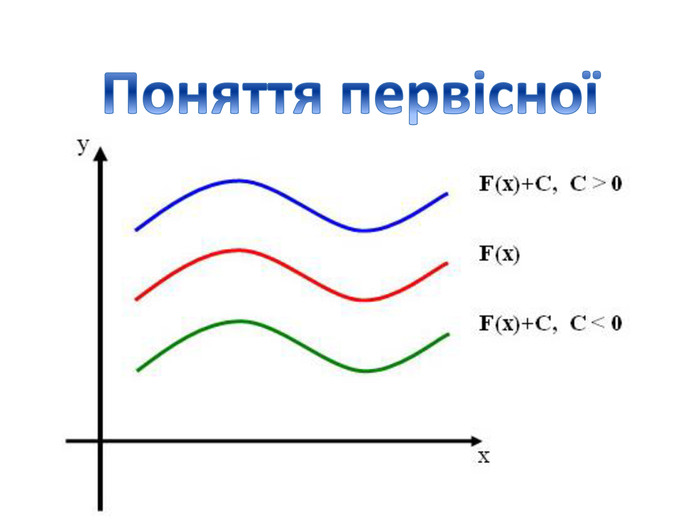
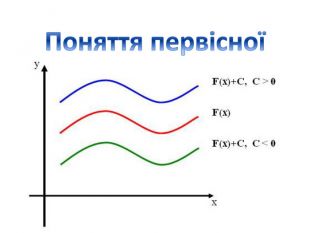
Презентація "Правила знаходження первісних. Первісна, що проходить через задану точку"
Про матеріал
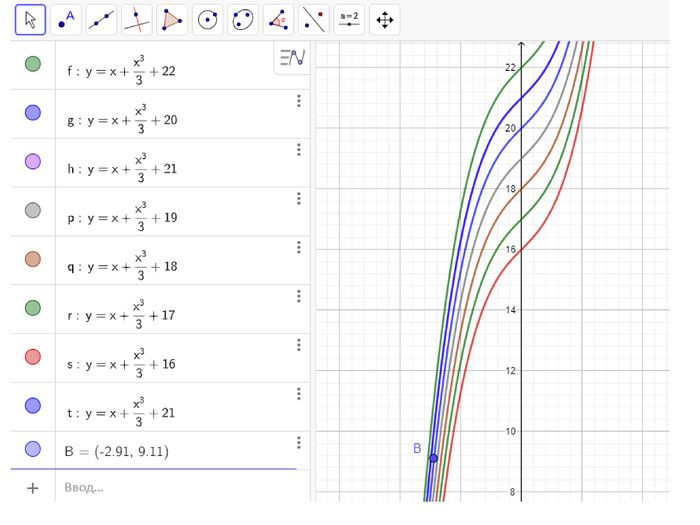
Презентація "Правила знаходження первісних. Первісна, що проходить через задану точку" містить розв'язки д прикладів з підручника Бевз Г.П. Математика 11 клас 
Перегляд файлу
Зміст слайдів
Номер слайду 1
Поняття первісної
Номер слайду 2
Параграф 13 Функція F(х) називається первісною для функції f(х) на проміжку І, якщо для кожного значення х із цього проміжка 𝐹/х=𝑓(х)
Номер слайду 3
Таблиця первісних. С – довільне число
Номер слайду 4
Правила інтегрування
Номер слайду 5
𝑓𝑥=−20𝑥3 𝐹𝑥=−20𝑥44+𝐶=−5𝑥4+𝐶 𝑓𝑥=−2𝑠𝑖𝑛𝑥 𝐹𝑥=−2−𝑐𝑜𝑠𝑥+𝐶=2𝑐𝑜𝑠𝑥+𝐶 𝑓𝑥=𝑥2+𝑒𝑥 𝐹𝑥=𝑥33+𝑒𝑥+𝐶 𝑓𝑥=−𝑥7−𝑒𝑥 𝐹𝑥=−𝑥88−𝑒𝑥+𝐶 Повторення
Номер слайду 6
Правила інтегрування𝑓𝑥=2𝑠𝑖𝑛𝑥 𝐹𝑥=2−𝑐𝑜𝑠𝑥+𝐶=−2𝑐𝑜𝑠𝑥+𝐶 𝑓𝑥=𝑠𝑖𝑛3𝑥 𝐹𝑥=13−𝑐𝑜𝑠3𝑥+𝐶=−13𝑐𝑜𝑠3𝑥+𝐶
Номер слайду 7
𝑓𝑥=𝑐𝑜𝑠7𝑥 𝐹𝑥=17𝑠𝑖𝑛7𝑥+𝐶=17𝑠𝑖𝑛7𝑥+𝐶 𝑓𝑥=5+𝑐𝑜𝑠𝑥 𝐹𝑥=5𝑥+𝑠𝑖𝑛𝑥+𝐶 𝑓𝑥=0,52𝑥 𝐹𝑥=12∙0,52𝑥𝑙𝑛0,5+𝐶 𝑓𝑥=𝑒−𝑥 𝐹𝑥=1−1𝑒−𝑥+𝐶=−𝑒−𝑥+𝐶
Номер слайду 8
𝑓𝑥=1+𝑥2 𝐹𝑥=1𝑥+𝑥33+𝐶=𝑥+𝑥33+𝐶
Номер слайду 9
Номер слайду 10
𝐹𝑥=1𝑥+𝑥33+𝐶=𝑥+𝑥33+𝐶 9=3+−333+𝐶 9−3−−273=𝐶 𝐶=9−3+9=15 𝐹𝑥=𝑥+𝑥33+15
Номер слайду 11
Домашні завдання:
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки
Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
-
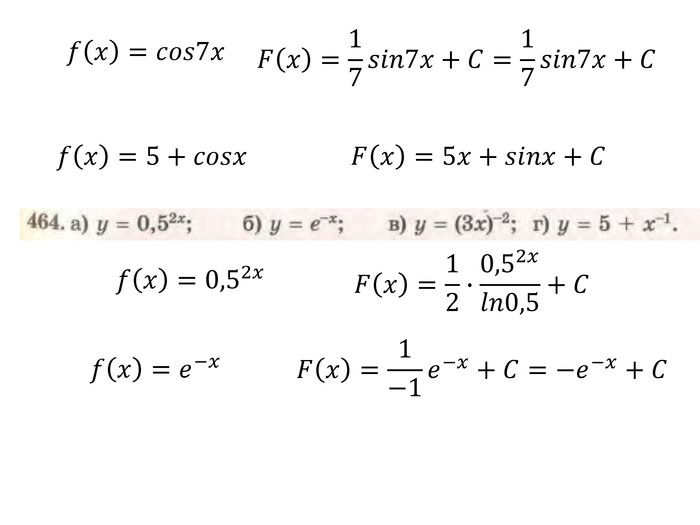
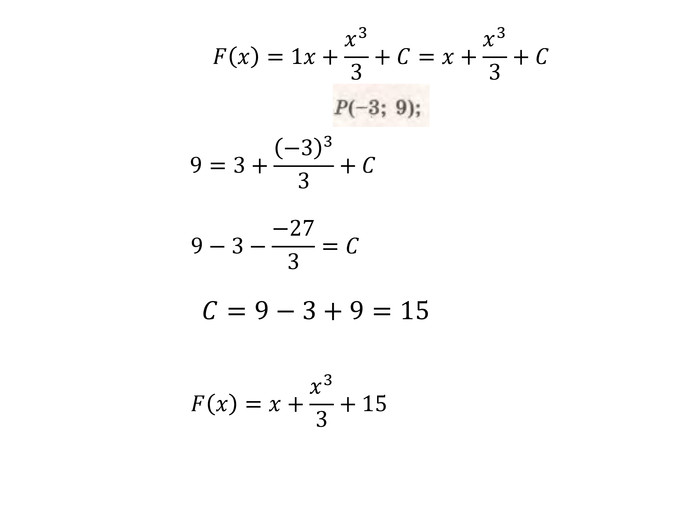
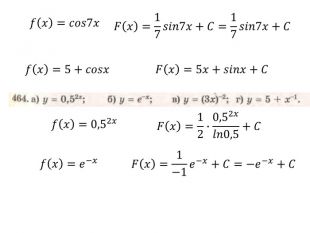
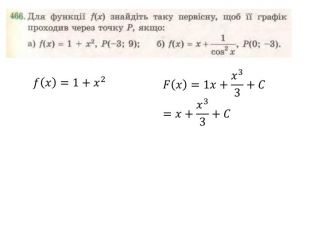
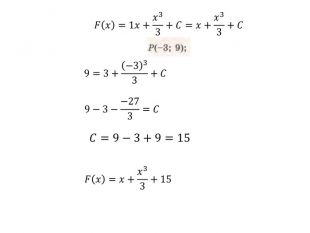
Андрейченко Тетяна Олексіївна
17.01.2024 в 22:06
Дякую! Змістовно і по суті.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-
Константинова Олена Павлівна
19.12.2022 в 18:07
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-
Лазорко Наталія Борисівна
16.01.2021 в 20:35
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-
Атаєва Лариса
10.01.2021 в 19:54
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
Показати ще 1 відгук