Презентація "Правильні многогранники"
Про матеріал
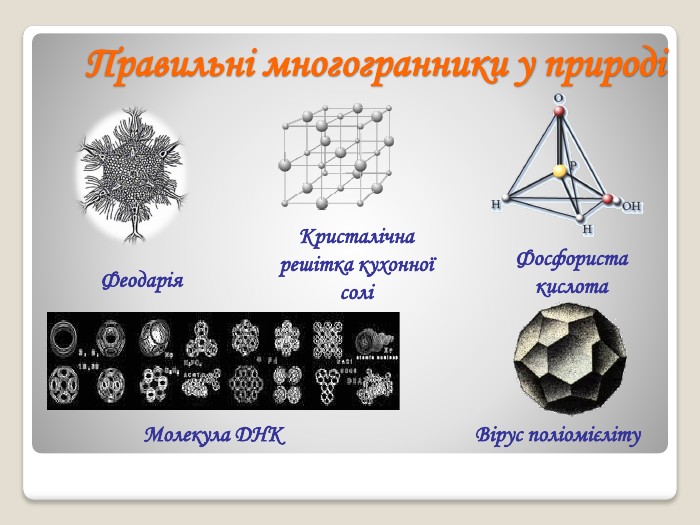
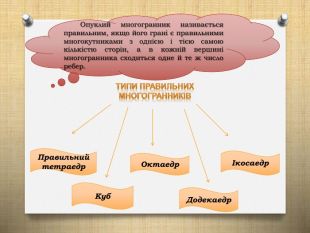
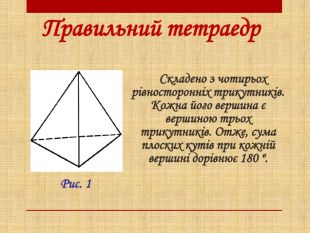
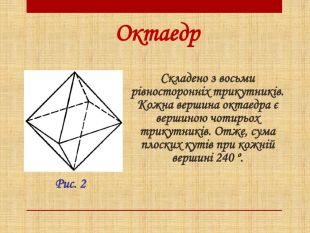
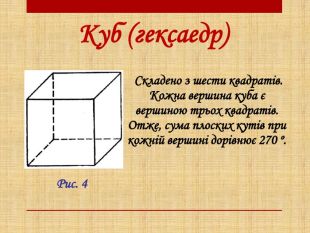
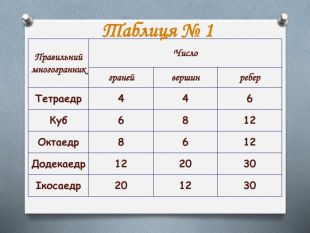
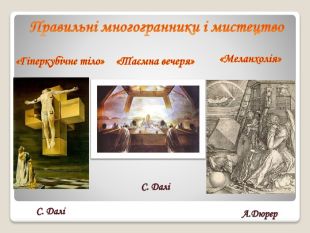
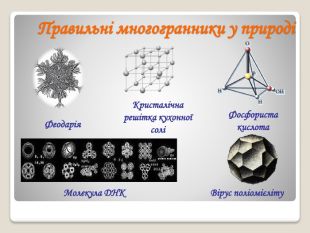
Презентація з геометрії на тему "Правильні многогранники". Формування поняття "правильні многогранники", ознайомлення здобувачів освіти з основними видами правильних многогранників, дослідження їх властивостей та зв’язок з навколишнім світом. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку