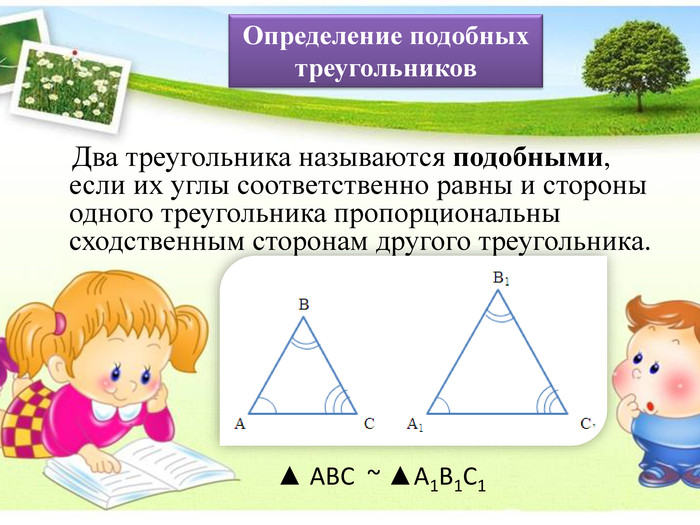
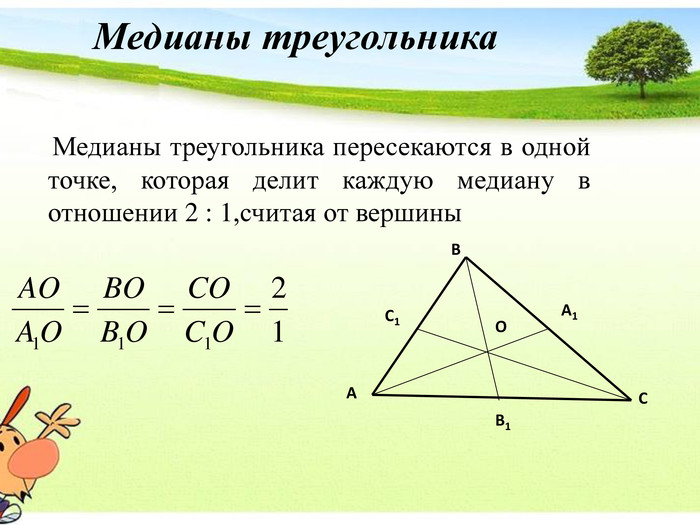
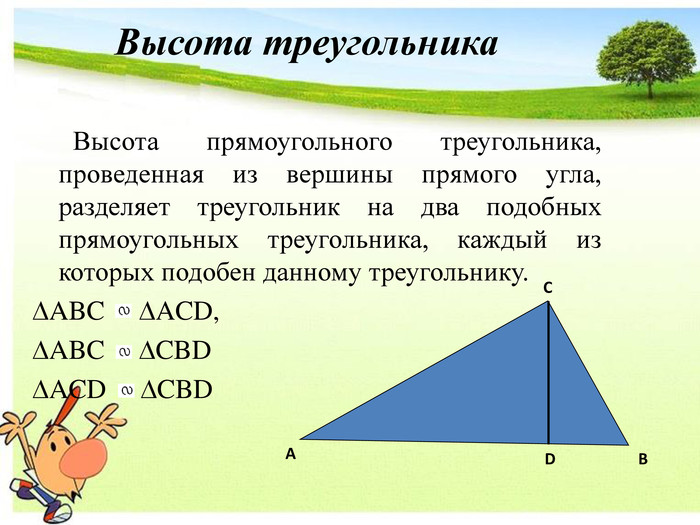
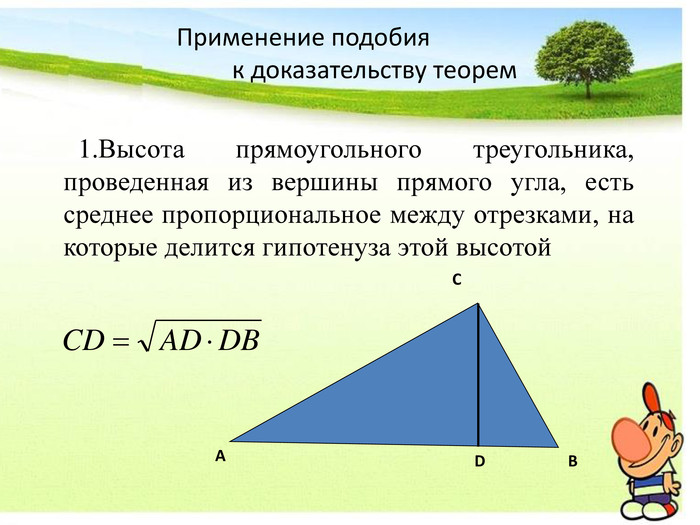
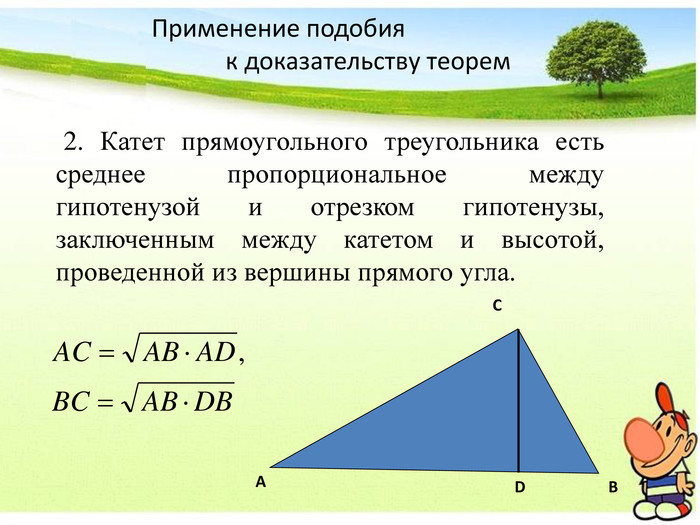
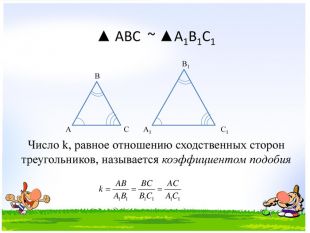
Презентация Признаки подобия треугольников
Про матеріал
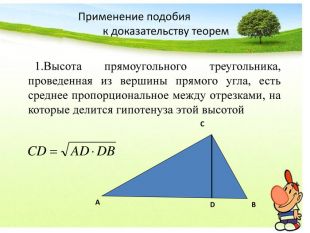
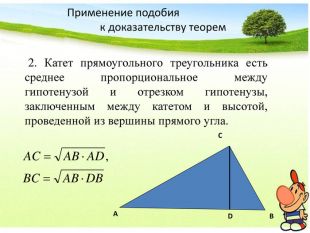
Презентация к уроку "Признаки подобия треугольников"- опережающее домашнее задание для учащихся. Работу выполнила ученица 8 класса Чмутова Аня Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку