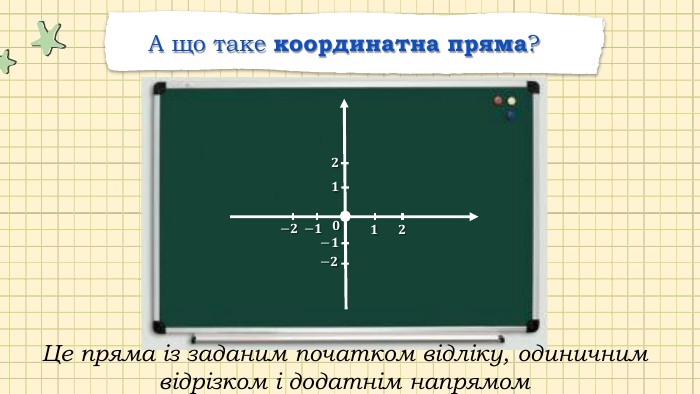
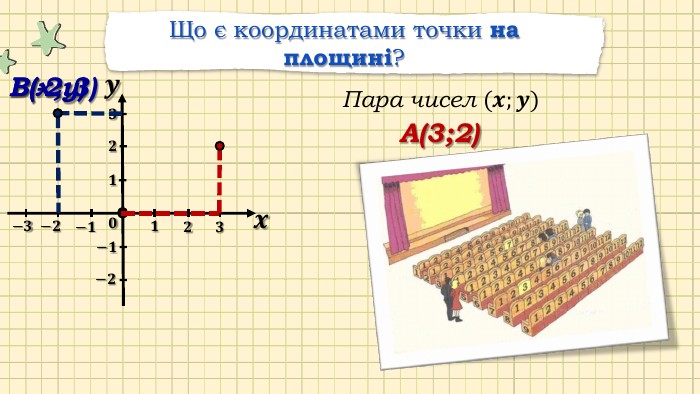
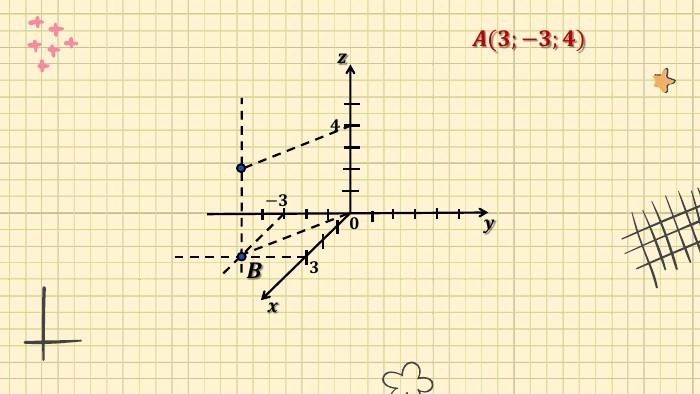
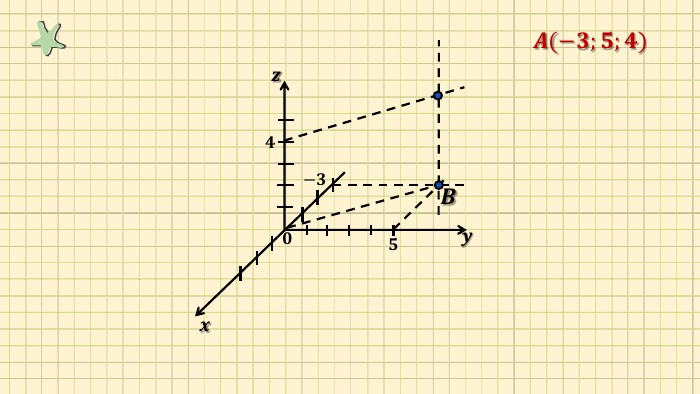
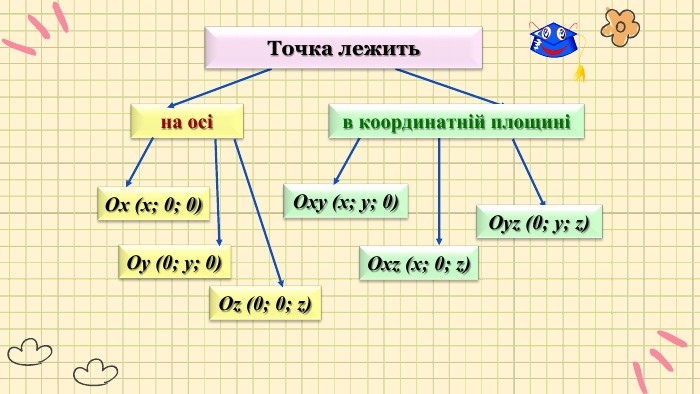
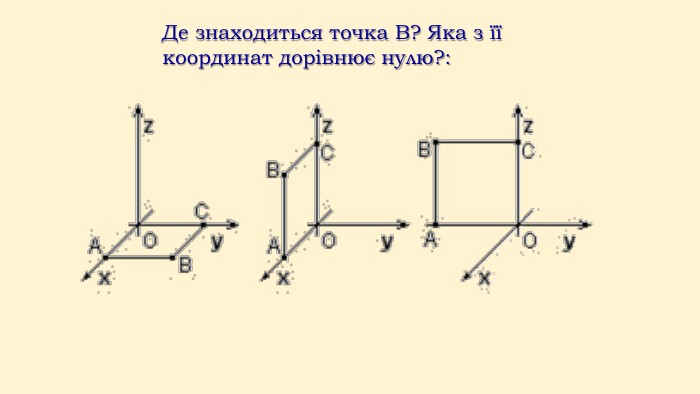
Презентація "Прямокутна система координат у просторі"
Про матеріал
Презентація до теми "Прямокутна система координат у просторі". Практичні задачі використано із підручника Математика, 10 (Істер) Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дуже гарна робота!
-


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку