Презентація "Раціональні дроби"
Про матеріал
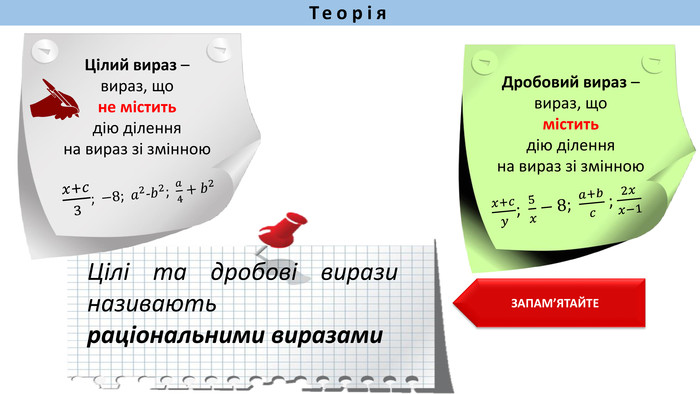
Презентація до уроку "Раціональні дроби" для учнів 8 класу. Містить теоретичний матеріал, приклади розв'язання типових завдань, а також тест для перевірки засвоєння матеріалу.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
























-

Кіріяк Наталія
06.04.2024 в 16:24
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Соломонюк Наталя
25.09.2022 в 20:42
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Володимирівна Валерія
25.09.2022 в 19:48
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

LM teacher
14.09.2022 в 22:06
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Матвій Галина
07.09.2022 в 08:52
Все продумано і цікаво організовано.
Дякую)
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Овчар Олена Анатоліївна
05.09.2022 в 11:24
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сімаченко Олена
04.10.2021 в 20:43
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Maria
21.09.2021 в 11:39
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Константинова Олена Павлівна
16.09.2021 в 21:34
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 6 відгуків