Презентація "Розв′язування найпрстіших тригонометричних рівнянь."
Про матеріал
За допомогою даної презентації здобувачі освіти зможуть навчитись розв′язувати найпрстіші тригонометричні рівняння,сформувати вміння та навички використовувати формули до розв’язування типових рівнянь; розвивати просторову уяву, логічне мислення, комунікативні вміння; виховувати почуття відповідальності за якість отриманих знань; формувати математичну та ключові компетентності, уміння вчитися впродовж життя, ініціативність та підприємливість, соціальну та громадянську компетентності. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра і початки аналізу (профільний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
До уроку
46. Рівняння cos х = b Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку









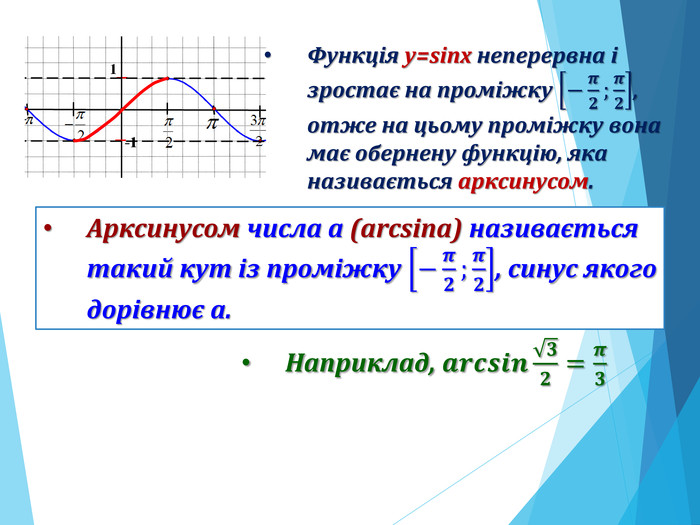
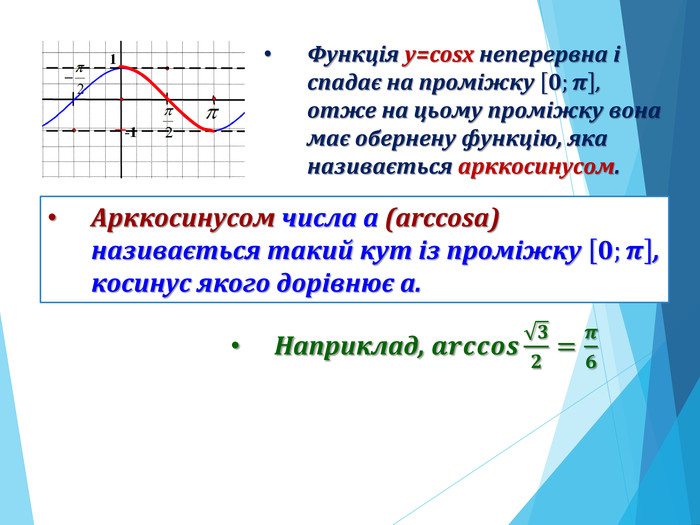
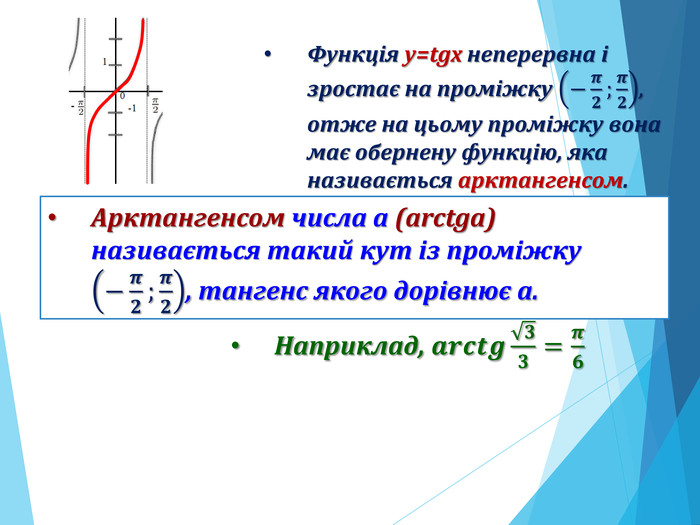
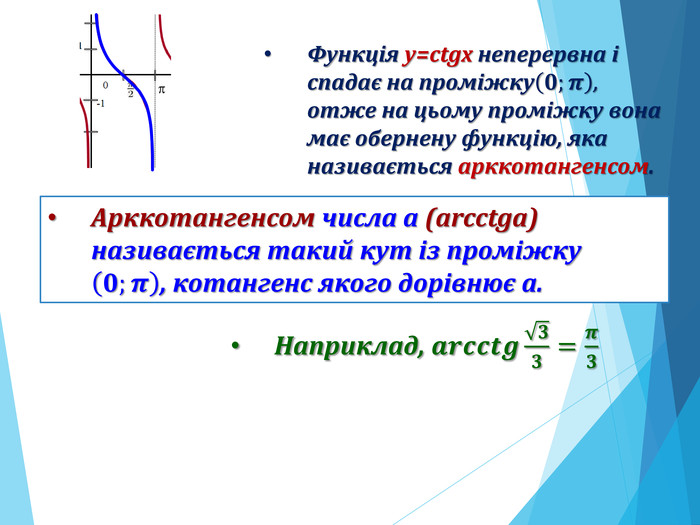
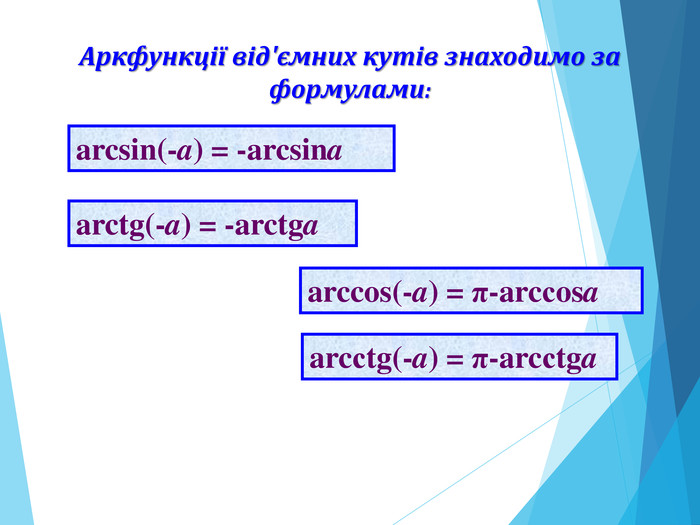




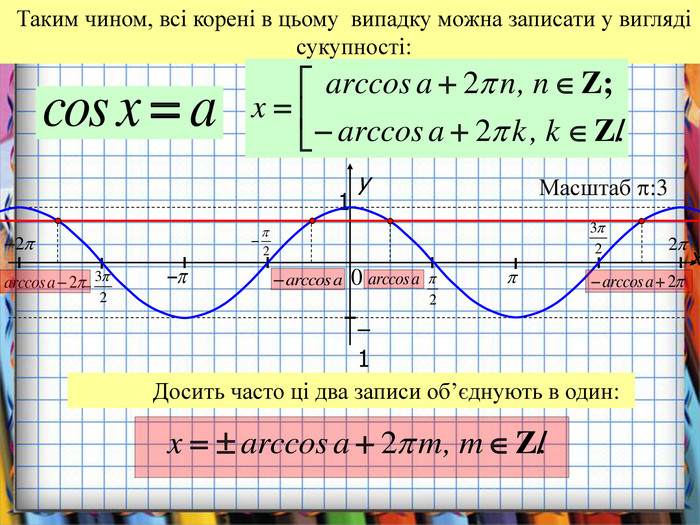
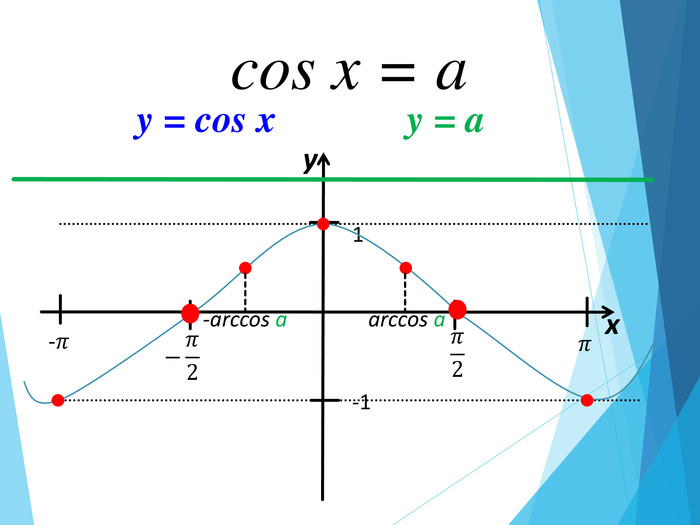
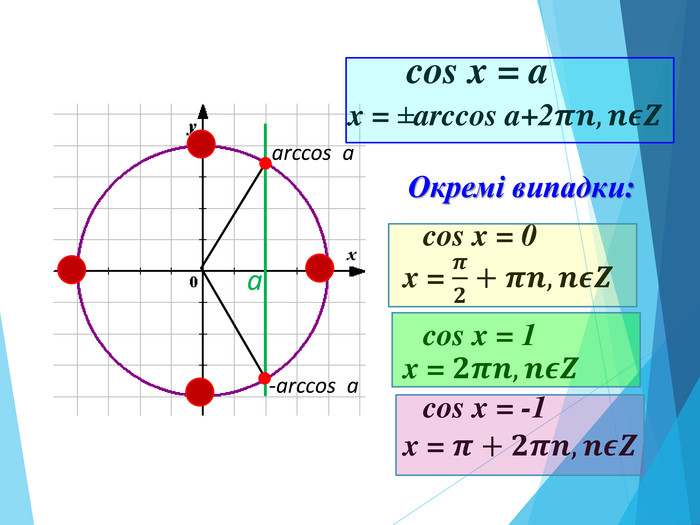
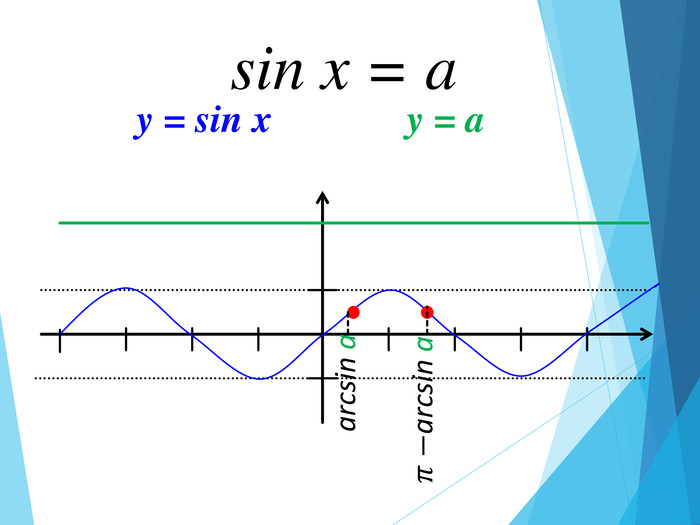
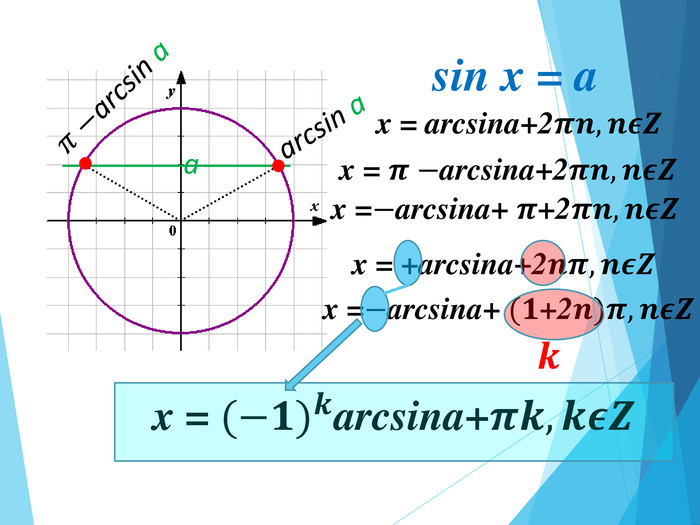
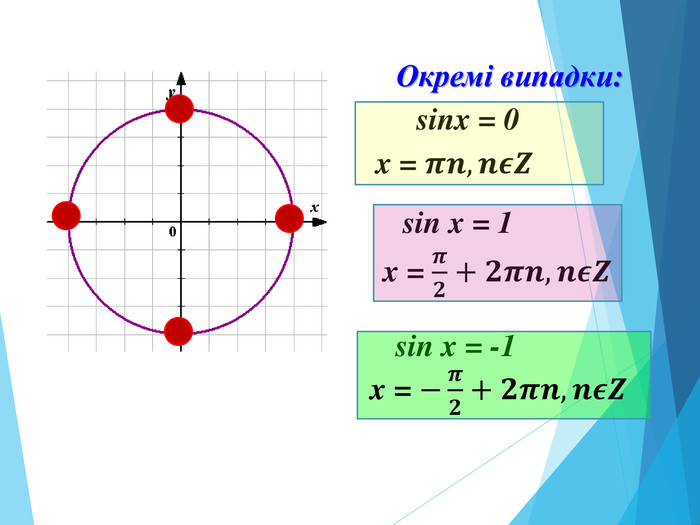
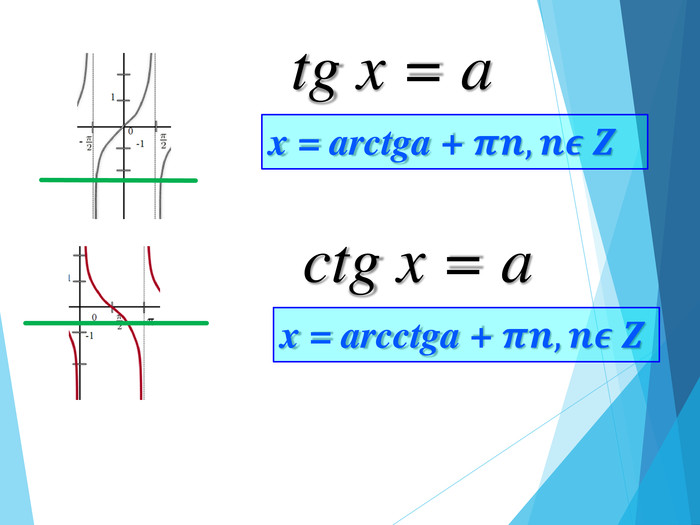








![Розв’язання будь-яких тригонометричних рівнянь зводиться до розв’язання найпростіших тригонометричних рівнянь, які ми розглянули вище. Для цього застосовуються відомі Вам тотожні перетворення, різні тригонометричні формули, різні способи розв’язування алгебраїчних рівнянь, формули скороченого множення и т.п. Отже, запам’ятайте : a[–1;1] Розв’язання будь-яких тригонометричних рівнянь зводиться до розв’язання найпростіших тригонометричних рівнянь, які ми розглянули вище. Для цього застосовуються відомі Вам тотожні перетворення, різні тригонометричні формули, різні способи розв’язування алгебраїчних рівнянь, формули скороченого множення и т.п. Отже, запам’ятайте : a[–1;1]](/uploads/files/195580/225899/241650_images/33.jpg)











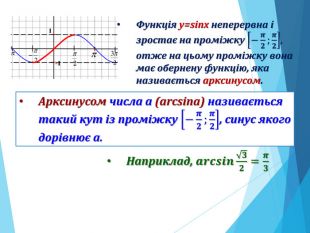
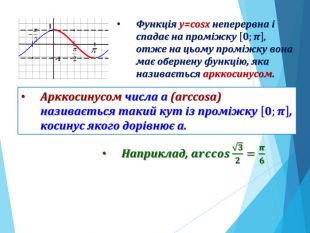







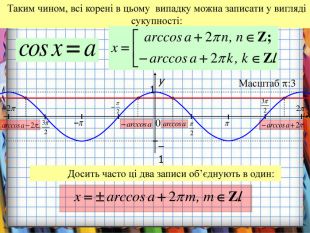
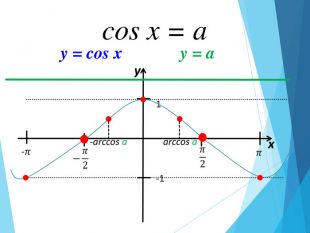
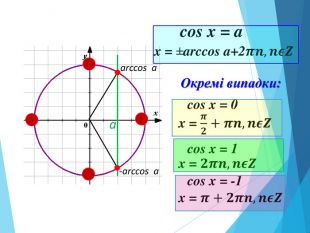
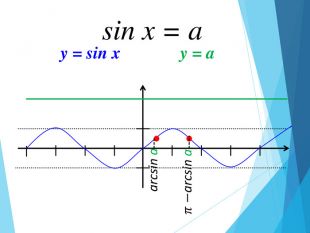
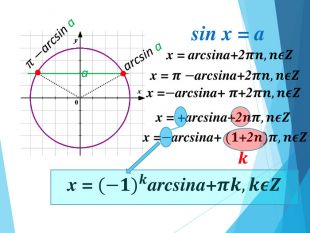
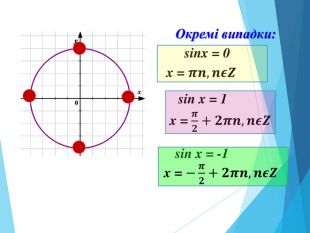
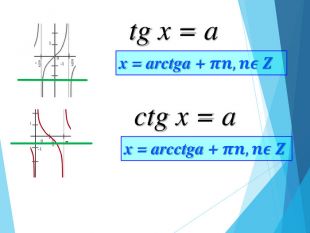


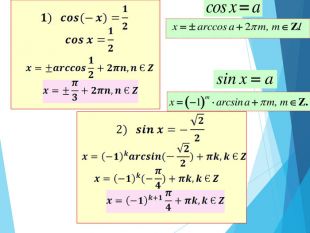









-

Литвиненко Анна Миколаївна
31.03.2024 в 14:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Клепікова Ольга Анатоліївна
11.03.2024 в 22:06
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Єлькіна Світлана Володимирівна
09.02.2024 в 06:29
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Водяницька Лариса
12.01.2024 в 17:07
Дуже змістовна презентація! Дякую!!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Левадній Сергій Павлович
17.05.2023 в 16:08
Шикарний почерк!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мячіна Надія Анатоліївна
28.02.2023 в 20:34
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Єременко Наталія Олексіївна
19.02.2023 в 20:11
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гелешко Наталія
18.02.2023 в 21:18
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кухтін Юлія Олександрівна
05.02.2023 в 10:04
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кухтін Юлія Олександрівна
05.02.2023 в 10:04
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кухтін Юлія Олександрівна
05.02.2023 в 10:04
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Демець Тетяна Юріївна
06.01.2023 в 19:38
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Катрін Альона Анатоліївна
14.04.2022 в 11:20
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 10 відгуків