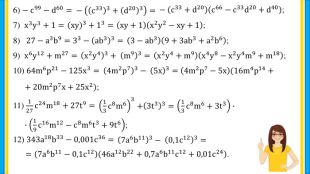Презентація "Розв'язування вправ № 1. Сума і різниця кубів".
Про матеріал
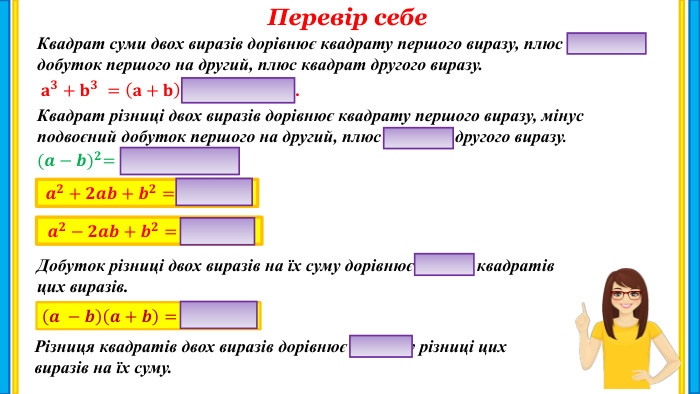
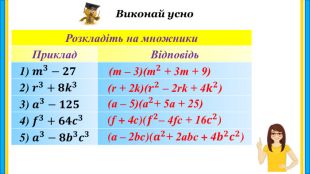
Матеріал містить завдання для продовження вивчення теми "Сума і різниця кубів" за підручником для 7 класу (НУШ) "Алгебра" закладів загальної середньої освіти/ О. С. Істер. Матеріал доцільно використовувати як на уроці, так і в позаурочній діяльності (якщо бажаєте, то матеріал можна змінювати, доповнювати та комбінувати з власним). Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку