Презентація "Розв*язування задач на складання системи двох рівнянь"
Про матеріал
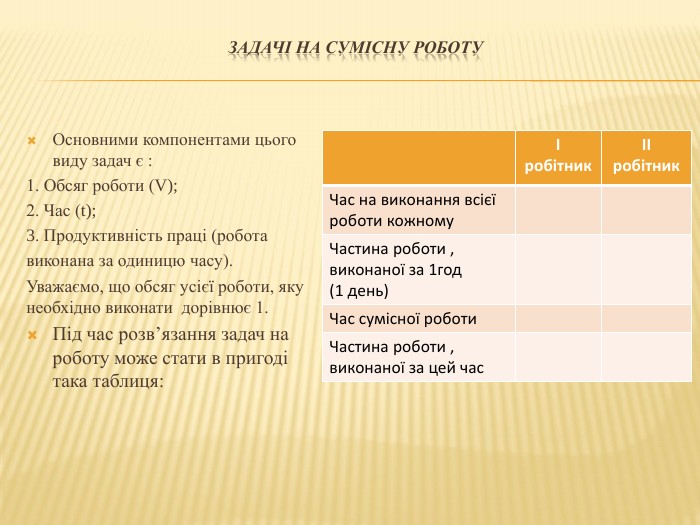
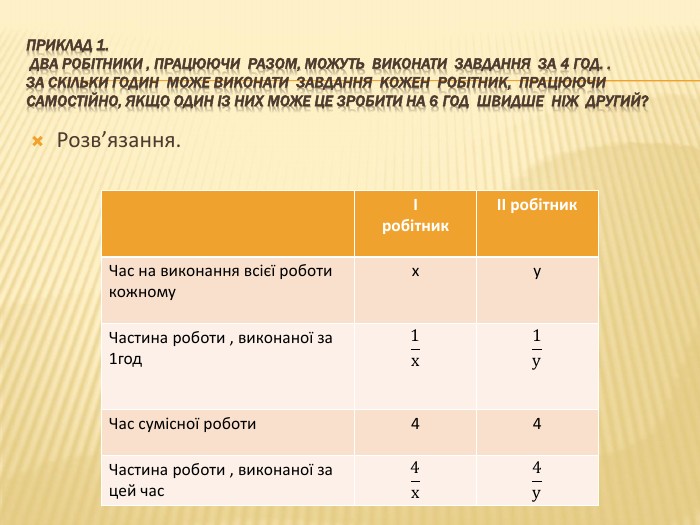
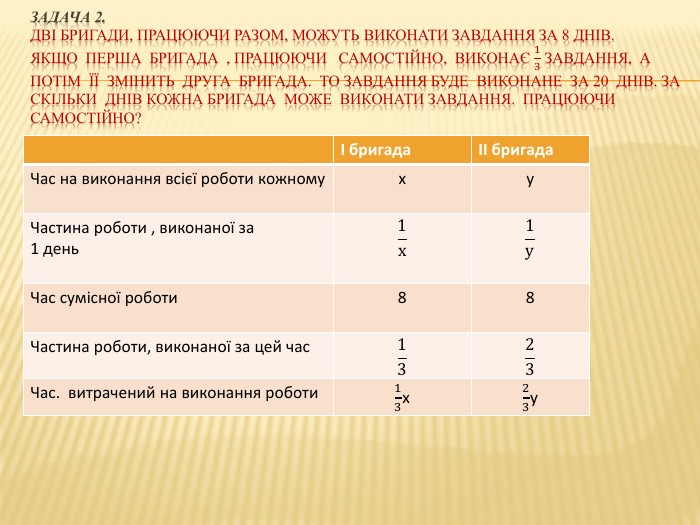
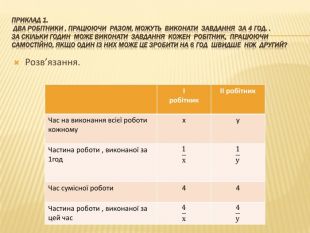
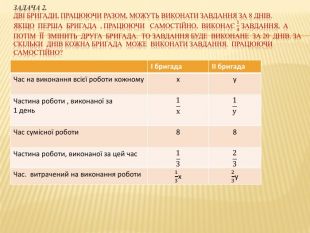
Презентація "Розв*язування задач на складання системи двох рівнянь" містить рекомендації до роз*язування задач різних типів та може бути використана при підготовці до контрольної роботи з цієї теми і підготовці до ДПА та ЗНО. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку