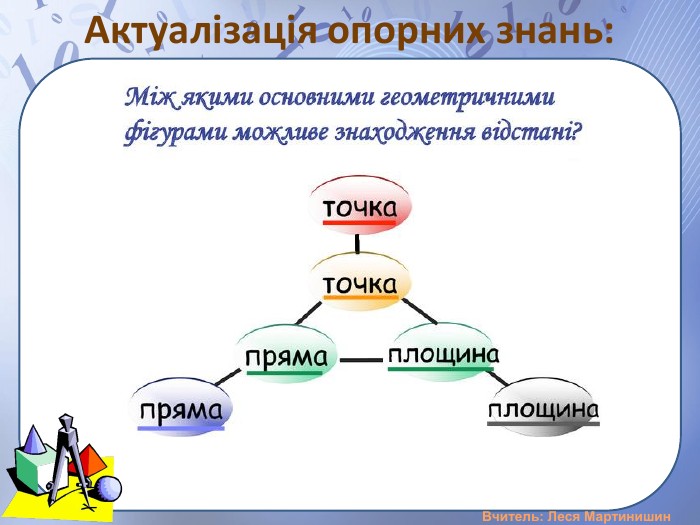
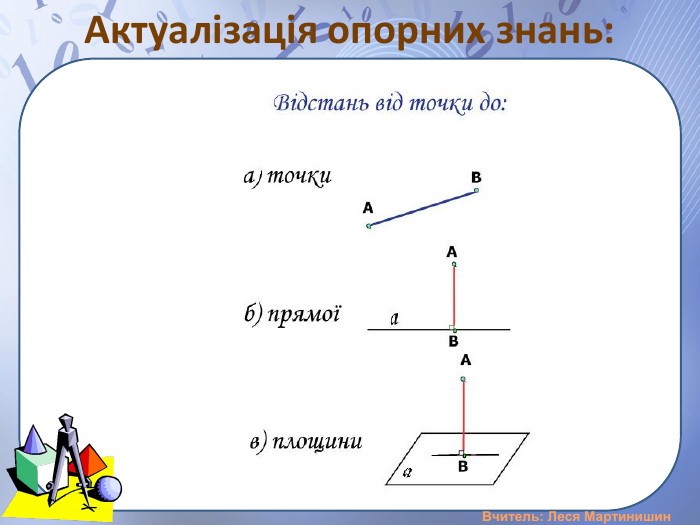
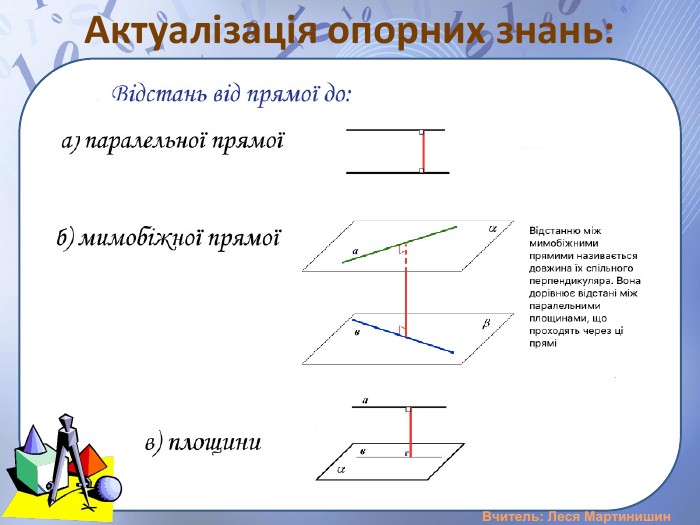
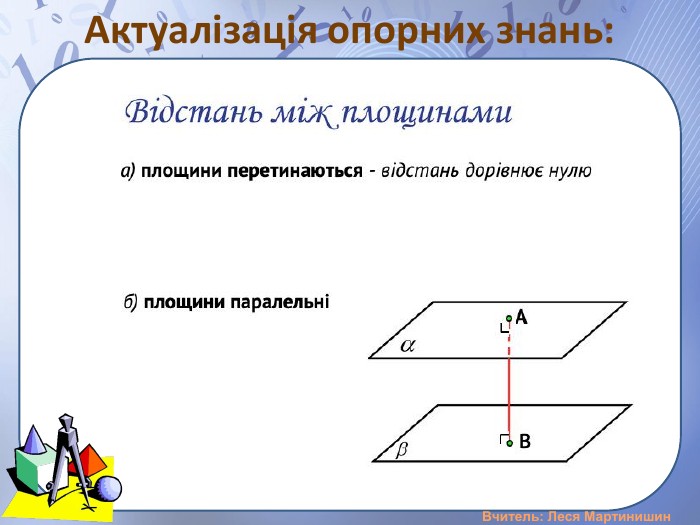
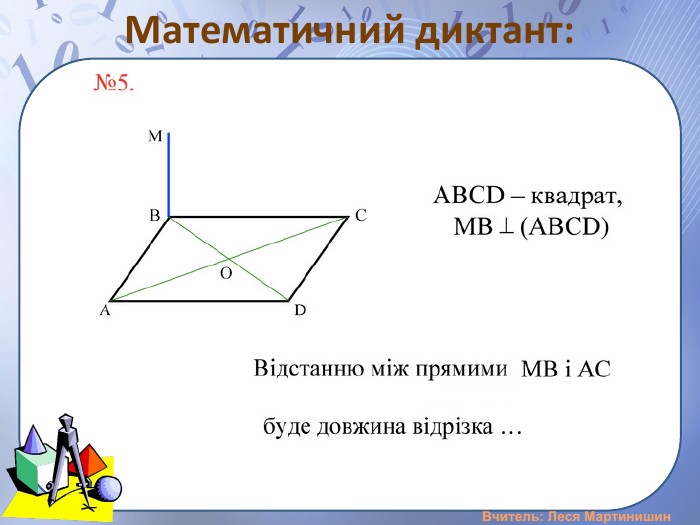
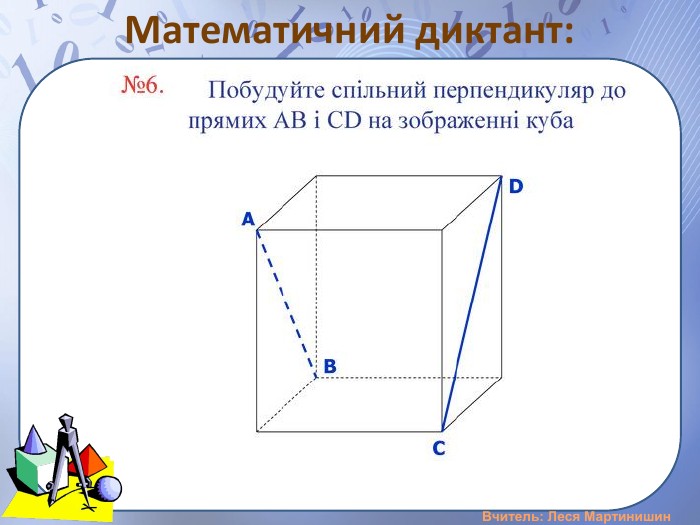
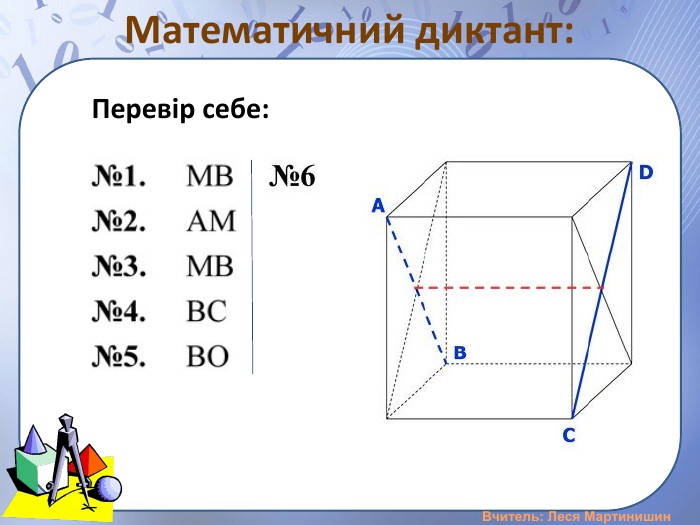
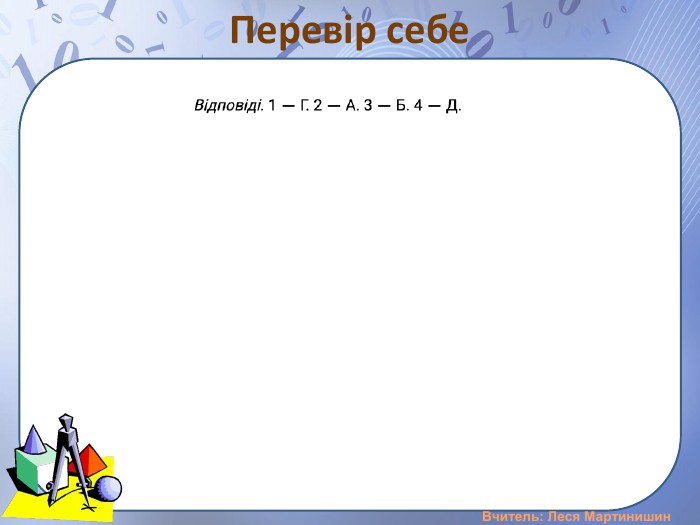
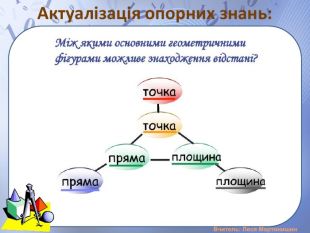
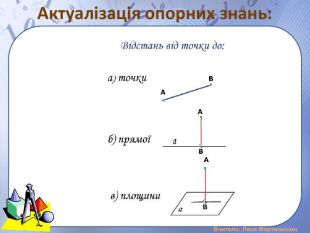
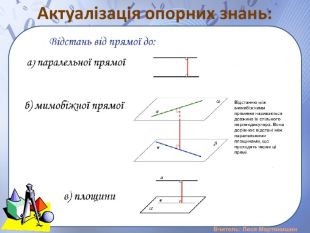
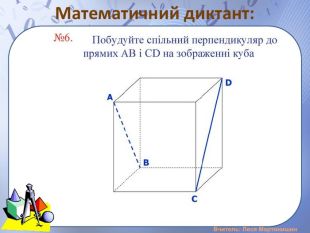
Презентація "Розв'язування задач на вимірювання відстані від точки до площини, між площинами, від прямої до площини"

Розв'язування задач на вимірювання відстані від точки до площини, між площинами, від прямої до площини. Вчитель: Леся Мартинишин. Підручник: Математика(Алгебра і початки аналізу та геометрія, рівень стандарту)О. С.Істер, 2018р.

Формування компетентностей:предметна компетентність: узагальнення знань учнів із теми “Відстані у просторі”; удосконалити вміння розв’язувати задачі з цієї теми;ключові компетентності:спілкування державною мовою - розуміти, пояснювати і перетворювати тексти математичних задач(усно і письмово);уміння вчитися впродовж життя - прагнути до вдосконалення результатів своєї діяльності;інформаційно-цифрова компетентність - визначати достатність данихдля розв’язання задач. Вчитель: Леся Мартинишин

Актуалізація опорних знань: Вчитель: Леся Мартинишин

Актуалізація опорних знань: Вчитель: Леся Мартинишин

Актуалізація опорних знань: Вчитель: Леся Мартинишин

Актуалізація опорних знань: Вчитель: Леся Мартинишин

Математичний диктант: Вчитель: Леся Мартинишин

Математичний диктант: Вчитель: Леся Мартинишин

Математичний диктант: Вчитель: Леся Мартинишин

Математичний диктант: Вчитель: Леся Мартинишин

Математичний диктант: Вчитель: Леся Мартинишин

Математичний диктант: Вчитель: Леся Мартинишин

Математичний диктант: Вчитель: Леся Мартинишин. Перевір себе:

Розв'язування задач. Вчитель: Леся Мартинишин. Розв’язання. Нехай ABCD - прямокутник, SО (ABC), SO = 3см, СD=AB= 4см, CAD = 30 .0 Трикутник AOB - рівносторонній: BAO = ABO = 90 - CAD = 90 - 30 = 60 ;0000 АОВ = 180 - (60 + 60 ) = 60 , як сума кутів трикутника.0000 Отже, АО = АВ = 4см. Розглянемо трикутник АОS: AOS = 90 . За теоремою Піфагора: * ; 9 + 16; AS = 5(см). 0 Відповідь: 5см. Точка О - центр описаного кола, за задачею 9.22; АО=ВО=R.

Вчитель: Леся Мартинишин. Розв'язування задач. Розв’язання. Нехай прямі a||b, К є a, К є b, КО NM, КM=13см, KN=15см, MN=14см. Розглянемо два прямокутні трикутники: KON і KOM. З теореми Піфагора: Нехай МО = х см, тоді NО = 14 - х см. 28 х = 140; х = 5. Отже, МО=5см; = 169-25; КО = 12 см. Відповідь: 12см.

Вчитель: Леся Мартинишин. Розв'язування задач. Розв’язання. Нехай ABCD - ромб, у якого АС=8 см, BD = 6 см; точка О - точка перетину діагоналей, центр вписаного кола. Проекція точки К є точка О за задачею 9.30 і КО = 1 см. За властивістю ромба АО = ОС = 8:2 =4(см); BO = OD = 6:2 = 3(см);ОМ - радіус кола, ОМ DC; ОD OC. З трикутника DOC теореми Піфагора: Нехай DM = х см, тоді СМ = 5-х см. З трикутників DMO i CMO теореми Піфагора: Отже, ; х=1,8. Отже, З КОМ за теоремою Піфагора: КМ = Відповідь: 2,6 см.

Вчитель: Леся Мартинишин. ЕКСПРЕС – КОНТРОЛЬ

Вчитель: Леся Мартинишин. Перевір себе

Оцінка власної участі у роботіВчитель: Леся Мартинишин

Домашня робота. Опрацювати §9; виконати №9.27, 9.34. Вчитель: Леся Мартинишин