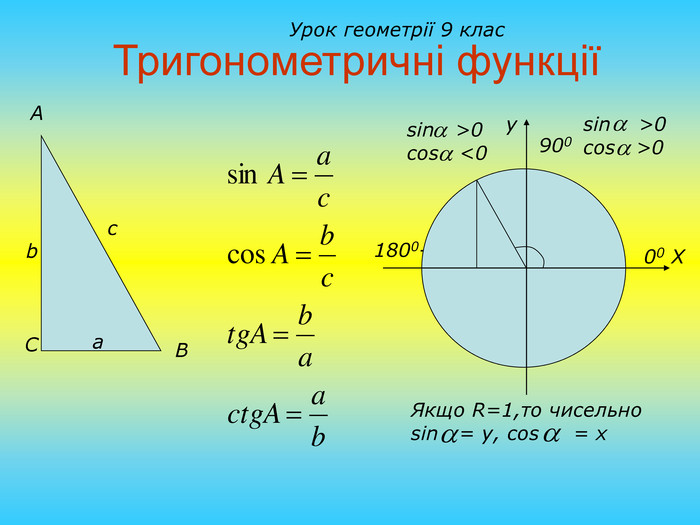
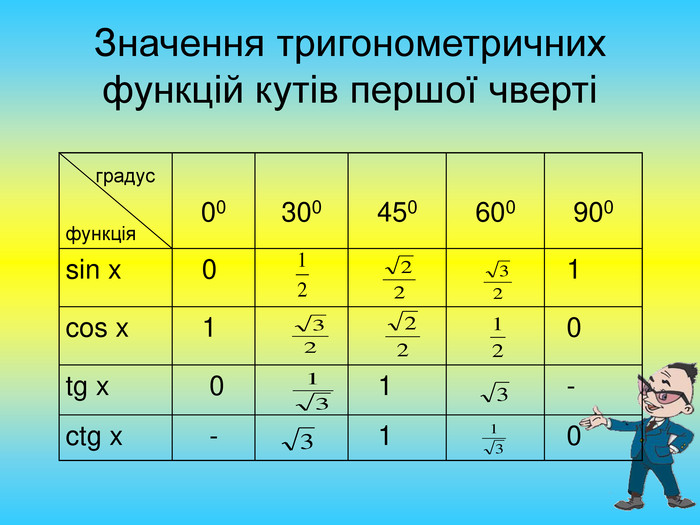
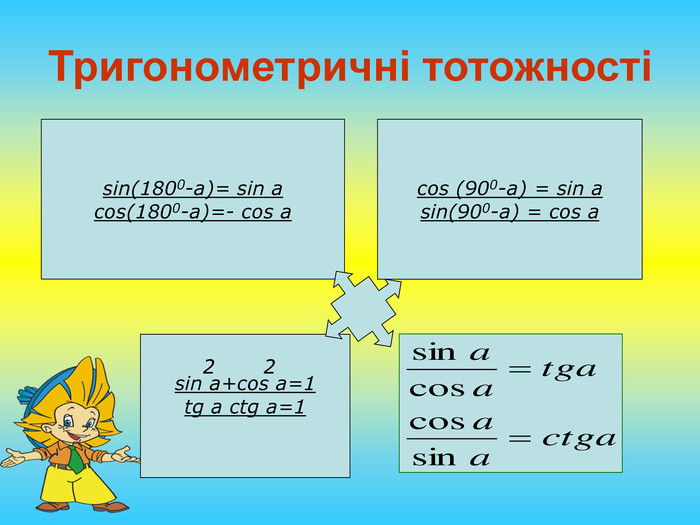
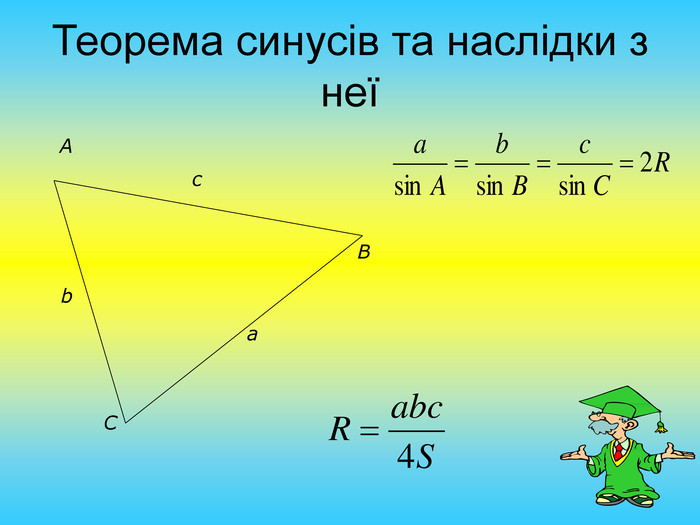
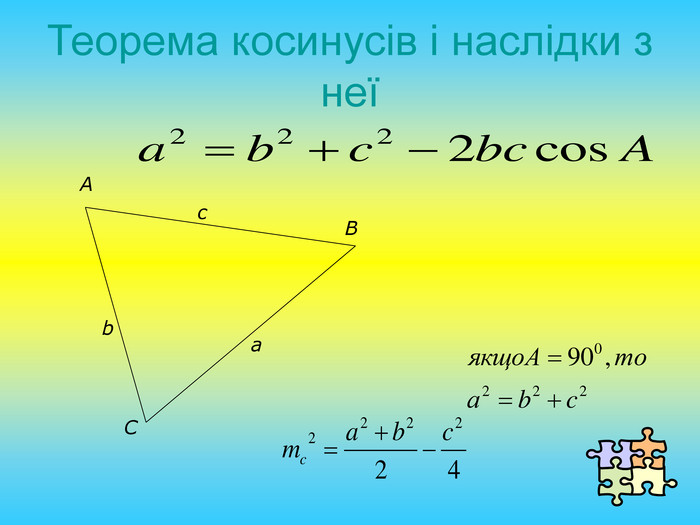
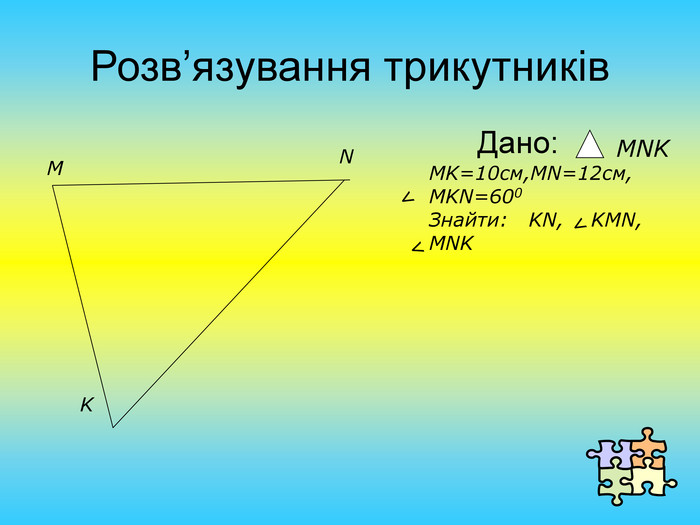
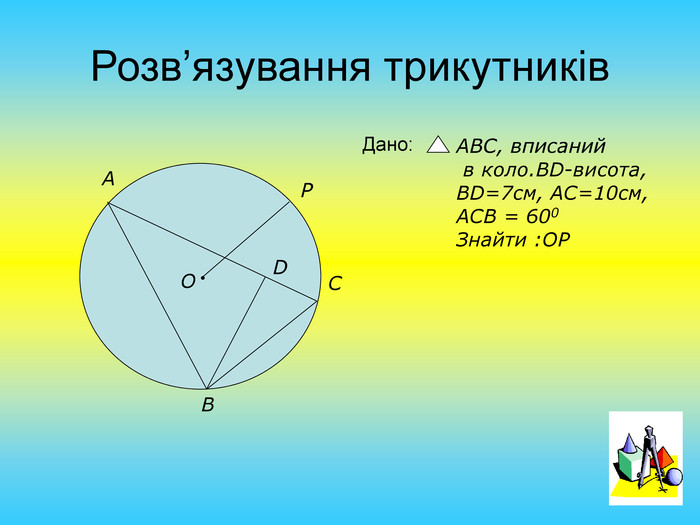
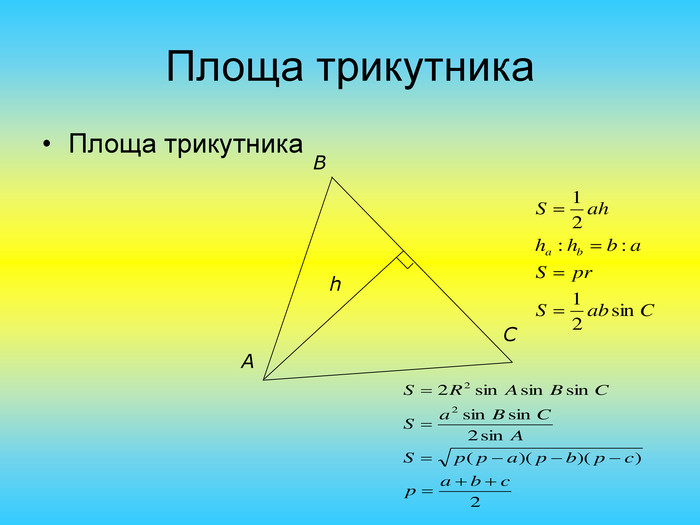
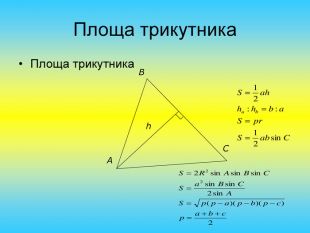
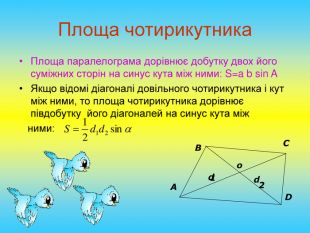
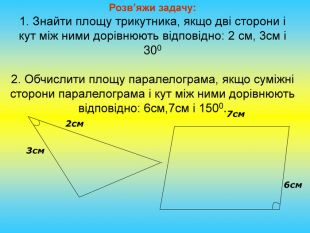
Презентація "Розв'язування задач на знаходження площі трикутника"

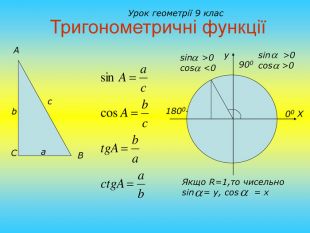
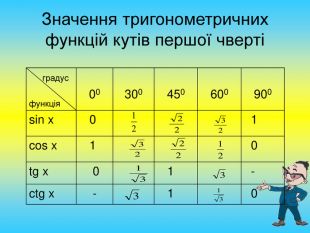
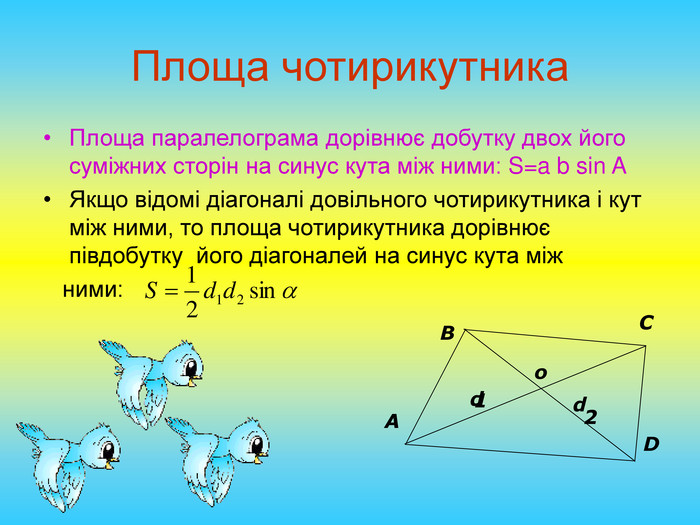
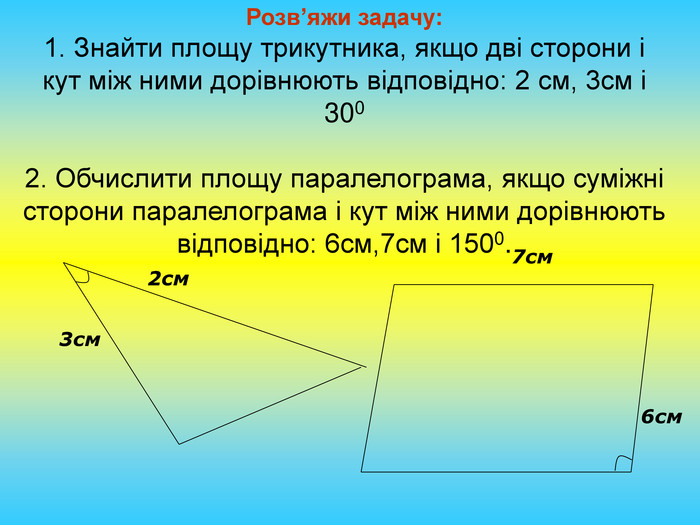
Мета: Повторити матеріал, вивчений на попередніх уроках. Продовжити формування навички розв’язувати задачі на обчислення площі трикутника, чотирикутника. Розвивати критичне мислення учнів в процесі розв’язування практичних задач. Урок геометрії 9 клас Тема: Розв’язування задач на знаходження площі трикутника

Урок геометрії 9 клас X y 900 1800- A B C a b c 00 sin >0 cos >0 sin >0 cos <0 Якщо R=1,то чисельно sin = у, cos = х Тригонометричні функції

0 - 0 1 900 1 - ctg x 1 0 tg x 1 cos x 0 sin x 600 450 300 00 градус функція Значення тригонометричних функцій кутів першої чверті

sin(1800-a)= sin a cos(1800-a)=- cos a cos (900-a) = sin a sin(900-a) = cos a sin a+cos a=1 tg a ctg a=1 2 2 Тригонометричні тотожності

А В С а с b Теорема синусів та наслідки з неї

A B C a b c Теорема косинусів і наслідки з неї

M N K MNK MK=10cм,MN=12cм, MKN=600 Знайти: KN, KMN, MNK < < < Розв’язування трикутників Дано:

A B C O D ABC, вписаний в коло.BD-висота, BD=7cм, AC=10cм, ACB = 600 Знайти :ОР Р Дано: Розв’язування трикутників

А В С h Площа трикутника Площа трикутника

d А В d о С D 1 2 Площа чотирикутника Площа паралелограма дорівнює добутку двох його суміжних сторін на синус кута між ними: S=a b sin A Якщо відомі діагоналі довільного чотирикутника і кут між ними, то площа чотирикутника дорівнює півдобутку його діагоналей на синус кута між ними:

2см 3см 7см 6см Розв’яжи задачу: 1. Знайти площу трикутника, якщо дві сторони і кут між ними дорівнюють відповідно: 2 см, 3см і 300 2. Обчислити площу паралелограма, якщо суміжні сторони паралелограма і кут між ними дорівнюють відповідно: 6см,7см і 1500.

Вчені Індії зводили розв’язування будь-яких трикутників до розв’язування прямокутних трикутників і не вимагали теорему синусів і косинусів.

Теорема синусів була доведена лише в одинадцятому столітті видатним астрологом Аль Біруні. Теоремою синусів користувалися, починаючи з ХVI століття і європейські математики.

Словесно теорема косинусів була вперше сформульована французьким математиком Француа Вієтом в ХVI столітті. Вієту належить виведення формули для синусів (або хорд) і косинусів кратних дуг. Великих успіхів досяг вчений у геометрії.

Підсумок уроку та повідомлення домашнього завдання Зверніться до тих завдань, які ми ставили на початку нашого уроку. Як ви думаєте, чи досягли ми поставленої мети? Проаналізуйте ситуації уроку. Що допомагало вам досягти успіху, щоб взяти це як рецепт на інші уроки, в повсякденне життя. Домашнє завдання: Завд.9 №4,5,6(б).