Проект "Трикутники у повсякденному житті"

Про матеріал

Вміння розв'язувати трикутники має широке практичне застосування у повсякденному житті, тому виникає потреба у глибокому і міцному засвоєнні теми.
Даний проект дає можливість узагальнити знання з теми «Розвʼязування трикутників», ознайомитися із змістом, різними доведеннями та наслідками з теореми синусів та теореми косинусів, розширити коло задач, що вирішуються із застосуванням даної теореми.
А також робота над проектом сприяє формуванню креативної компетентності учнів, створює оптимальні умови для їх самореалізації, розкриття творчого потенціалу та допомагає в реалізації життєвих планів особистості школяра.

Перегляд файлу

ПРОЕКТ

«Трикутник у повсякденному житті»

Технологічний паспорт навчального проекту

Проблема та її актуальність

Проблема. Необхідно знайти відстань між двома недоступними пунктами. Як звести задачу спостереження за об'єктом С до задачі розвʼязання трикутника АВС?

Актуальність. Трикутник – одна з перших геометричних фігур, про властивості якої людство дізналося ще в давнину. Задачі про трикутник знаходять у давньоєгипетських папірусах, старовинних індійських книгах. Чому ж трикутник цікавив людей з давніх часів? І який діапазон застосувань трикутників у різних сферах діяльності людини сьогодні? Відповіді на ці запитання учні знайдуть працюючи над проектом.

Учні 9 класу вивчають теорему косинусів і теорему синусів, але одним із недоліків у вивченні теорем та їх доведень є формалізм у знаннях і вміннях учнів. Частина дітей сумлінно заучує доведення теорем за підручником, але не може відтворити їх на зміненому положенні рисунка, з іншими буквеними позначеннями. І, що найголовніше, учні часто не вміють застосовувати теорему у конкретних ситуаціях, не вміють самостійно знаходити доведення теореми навіть у найпростіших випадках.

Вміння розв’язувати трикутники має широке практичне застосування у повсякденному житті, тому виникає потреба у глибокому і міцному засвоєнні теми.

Даний проект дає можливість узагальнити знання з теми «Розвʼязування трикутників», ознайомитися із змістом, різними доведеннями та наслідками з теореми синусів та теореми косинусів, розширити коло задач, що вирішуються із застосуванням даної теореми. А також робота над проектом сприяє формуванню креативної компетентності учнів, створює оптимальні умови для їх самореалізації, розкриття творчого потенціалу та допомагає в реалізації життєвих планів особистості школяра.

Тема: Трикутник у повсякденному житті
Автори розробники:

Білусяк Лідія Василівна, вчитель Манявського НВК

Цільова аудиторія: проект пропонується для реалізації з учнями 9 класу під час вивчення теми «Розв’язування трикутників».
Мета:

виробити у школярів практичні навички розвʼязування трикутників для вирішення практичних потреб;
розширити знання учнів про трикутник та способи його розвʼязання;
поглибити та систематизувати знання учнів про теорему синусів, теорему косинусів та наслідків з них;
сприяти усвідомленню важливості даної теми;
розвивати логічне мислення, вміння здійснювати доказові міркування та вміння виділяти головне, істотне в досліджуваному матеріалі;
розвивати вміння співпрацювати в групах, проявляти ініціативу, робити висновки;
виховувати спостережливість, науковий підхід, та інтерес до математики.

Завдання:

Ознайомитися з історичними відомостями про теорему синусів і косинусів.
Узагальнити типи задач на розвʼязування трикутників та методи їх вирішення.
Дослідити застосування прийомів розвʼязування трикутників для вирішення практичних задач.
Знайти застосування даної теми у нестандартних ситуаціях.
Навчитися розвʼязувати трикутники засобами табличного процесора.

Передбачувані (очікувані) результати: Реалізація наскрізних ліній «Екологічна безпека та сталий розвиток» і «Підприємливість та фінансова грамотність» та формування таких ключових компетентностей: спілкування державною мовою, математична, компетентності у природничих науках і технологіях, інформаційно-цифрова, уміння вчитися впродовж життя, ініціативність і підприємливість, соціальна і громадська, обізнаність і самовираження у сфері культури.
Кінцевий результат: збірник практично-орієнтованих задач з теми «Розвʼязування трикутників» з історичною довідкою, теоретичними відомостями, основними прийомами розвʼязання трикутників та завданням для самоперевірки і самоконтролю.
Характеристика проекту:

Спосіб (харектеристика) діяльності: дослідницько-пошуковий, практико-орієнтований.

Зміст: проект складається з таких етапів:

Підготовчий: учитель коментує тему і мету проекту. Мотивує діяльність учнів. Обговорює цілі і головні питання проекту.
Моделюючий. Учні об’єднуються в групи: Історики (дізнаються причини зародження тригонометрії як науки та вивчають історичні відомості про теорему синусів і косинусів); Теоретики (узагальнюють типи задач на розвʼязування трикутників та алгоритми знаходження невідомих елементів трикутника); Дослідники (досліджують застосування знань з теми для вирішення прикладних задач), Допитливі (знаходять застосування даної теми у нестандартних ситуаціях), Практики (ровʼязують задачі засобами табличного процесра).
Діяльнісний. Відбувається збір інформації з теми «Розвʼязування трикутників», пошук відповідей на основні питання з подальшим обговоренням, аналізом та корекцією. Кожна група обирає питання та відповідає на них.
Заключний. Презентація по даному проекту.

Склад учасників: учні 9 класу

Тривалість: середньої тривалості – 2 тижні

Характеристика партнерської взаємодії: груповий.

Реалізація міжпредметних звʼязків: міжпредметний - проект об’єднує історію, математику, географію та інформатику.

Механізм реалізації проекту (план дій)

№з/п	Назва заходу	Термін виконання	Виконавці	Ресурси
№з/п	Назва заходу	Термін виконання	Виконавці	матеріальні	людські
	Постановка проблеми.	перший день	керівник проекту	+	+
	Визначення теми та мети проекту.	перший день	керівник проекту		+
	Ознайомлення учнів із суттю проекту та основними етапами його реалізації.	перший день	керівник проекту		+
	Формування проектних груп.	перший день	учасники проекту		+
	Видача письмових рекомендацій авторам.	перший день	керівник проекту	+
	Пошук відповідей на тематичні питання.	1 тиждень	учасники проекту	+	+
	Проміжні звіти учнів.	протягом першого тижня	керівники груп	+	+
	Узагальнення результатів досліджень.	протягом другого тижня	учасники проекту	+	+
	Індивідуальні і групові консультації за змістом і правилами оформлення проектних робіт.	протягом другого тижня	керівник проекту і керівники груп		+
	Оформлення результатів.	протягом другого тижня	учасники проекту	+	+
	Створення звіту у вигляді презентації, рефератів, тощо.	в кінці другого тижня	учасники проекту	+	+
	Підготовка до публічного захисту.	в кінці другого тижня	учасники проекту		+
	Координаційна нарада осіб, відповідальних за захід.	останній день другого тижня	керівник проекту і керівники груп		+
	Публічний захист проектів.	початок третього тижня	учасники проекту		+
	Підбиття підсумків, аналіз виконаної роботи.	після захисту	керівник і учасники проекту	+	+
	Підсумковий етап. Подяки учасникам, узагальнення матеріалів, оформлення звітів про виконану роботу.	після захисту	керівник і учасники проекту	+	+

Аналіз силового поля

Підтримка	Бал	Опір	Бал
Адміністрація	10	Адміністрація	0
Психолог	10	Психолог	0
Учителі початкових класів	5	Учителі початкових класів	5
Педагог-організатор	10	Педагог-організатор	10
Учні	5	Окремі учні	5
Батьки	5	Окремі батьки	5

ВИСНОВОК: цей проект має певну підтримку, яка є більшою за опір, тому вважаємо його життєздатним у подальшому впровадженні

Оцінювання

Параметри оцінки проекту:

обсяг і повнота розробок, виконання етапів проекту, самостійність, закінченість, підготовленість проекту до сприйняття іншими людьми, матеріальна реалізація проекту;
рівень творчості, оригінальність теми, рішень, підходів;
якість, оформлення, відповідність, практичність продуктів діяльності;
досконалий захист проекту: якість та повнота доповіді, аргументованість, переконливість, обсяги та глибина знань по темі, ерудиція, використання наочних засобів, готовність до дискусії.

Приклад продукту, який можуть запропонувати учні

Історичні відомості

Трикутник є першою фігурою, яка не може розкластися в інший вигляд більш простої фігури… і тому є першим фундаментом будь-якої речі, яка має границю й форму.

Джордано Бруно

Теорема косинусів відома ще стародавнім грекам. У твердженнях 12 і 13 другої книги «Начал» Евкліда розглянуто питання про квадрат сторони трикутника, яка лежить проти гострого і проти тупого кута.

Вчені Індії, зводили розв’язування будь-яких трикутників до розв’язування прямокутних трикутників і не потребували теорему синусів і не знали її. Безпосередньо для плоских трикутників теорему косинусів довів арабський астроном і математик Абу-л-Вафа (940-998). Дещо пізніше доводить і використовує цю теорему знаменитий середньоазіатський учений-енциклопедист Ал-Біруні (973-1048).

В Європі теорему косинусів по-справжньому оцінив і почав систематично використовувати знаменитий французький алгебраїст Франсуа Вієт (1540-1603).

Вважають, що теорему синусів вперше довів учитель Ал-Біруні, іранський математик Ібн-Ірак. Доведення цієї теореми зустрічається і в працях Ал-Біруні.

Сучасний вид теорема косинусів приймає в 1801 році у французького математика Лазара Карно.

Теореми косинусів і синусів взаємопов'язані. З кожної з них можна вивести іншу, виконавши відповідні тригонометричні співвідношення.

Назви ліній синуса та косинуса уперше були введені індійськими вченими. Вони ж склали перші таблиці синусів і в Індії починається по суті вчення про тригонометричні величини, назване пізніше гоніометрією.

Найпершою тригонометричною функцією була хорда, що відповідає своїй дузі. Для цієї функції були побудовані перші тригонометричні таблиці (II ст. до н. е.) для потреб астрономії.

Далі уперше в історії науки в період V–XII ст. індійські математики й астрономи замість повної хорди стали розглядати половину, яка відповідає сучасному поняттю синуса. Величину половини хорди вони назвали «архиджива», що означало «половина тятиви лука». Окрім sin(x), індійці розглядали також величину 1 – cos(x), яку вони називали «комаджива», і величину cos(x) – «котиджива».

Подальший розвиток вчення про тригонометричні величини отримало в IX-XV ст. у країнах Середнього і Ближнього Сходу в працях ряду математиків, які не лише скористалися досягненнями, що існували у той час, в цій області, але і зробили свій значний внесок у науку.

Також Ф. Вієт встав у витоків створення нової науки – тригонометрії. Багато тригонометричних формул уперше було записано цим науковцем. У 1593 році він першим сформулював в словесній формі теорему косинусів. З інших відкриттів Вієта слід зазначити вираження для синусів і косинусів кратних дуг через sin(x) і cos(x).

Поняття таких тригонометричних функцій, як тангенс, котангенс, секанс і косеканс, визначив абсолютно строго, виходячи з розгляду тригонометричного кола, іранський математик Абу-ль-Вефа. Сучасні назви цих функцій були дані в період з XV по XVII століття європейськими ученими. Так, термін «тангенс» з латинської «дотична» був введений в XV столітті засновником тригонометрії в Європі Регіомонтаном (німецьким астрономом і математиком Йоганном Мюллером (1436-1476)). У XVI столітті Фінк вводить термін «секанс». У XVII столітті помічник винахідника десяткових логарифмів Бріггса вчений Гюнтер вводить назву «косинус» і «котангенс», причому префікс «ко» (co) означає доповнення (complementum). Сучасні позначення синуса і косинуса знаками sin(x) і cos(x) були уперше введені в 1739 році І. Бернуллі в листі до петербурзького математика Л. Ейлера. Дійшовши висновку, що ці позначення дуже зручні, він став вживати їх у своїх математичних роботах. Крім того, Ейлер вводить наступні

скорочення для позначень тригонометричних функцій кута x: tang(x), cot(x), sec(x), cosec(x).

Найдавніше із доведень теореми синусів, що дійшли до нас, на площині описано в книзі Насир Ад-Дин Ат-Тусі «Трактат про повний чотиристоронник» (XIII ст.).

Теорема синусів для сферичного трикутника була доведена математиками середньовічного Сходу ще в X столітті. У праці Ал-Джайяни XI століття «Книга про невідомі дуги сфери» наводилося загальне доведення теореми синусів на сфері.

У 10 ст. багдадський вчений Мухаммед з Буджана, відомий під ім'ям Абу-ль-Вефа сформулював теорему синусів. Насир-ед-Дин з Туса (1201-1274) систематично розглянув усі випадки розв’язування косокутних сферичних трикутників і вказав ряд нових способів. У 12 ст. був перекладений з арабського на латинь ряд астрономічних робіт, що дозволило ознайомитися з ними європейцям. До речі, саме Регіомонтан через 200 років після Насир-ед-Дина заново відкрив його теореми.

Друге формулювання теореми косинусів

Часто задача, яку потрібно розв’язати, серед даних елементів не містить кутів, відповідь також не потребує знання кутів. У цих випадках виведення величин відповідних кутів і відповідних тригонометричних виразів не є обов’язковим. У підручниках з геометрії для подібних ситуацій наведене друге формулювання теореми косинусів.

Теорема. 1) Квадрат будь-якої сторони трикутника, що лежить проти гострого кута, дорівнює сумі квадратів двох інших сторін мінус подвоєний добуток однієї з цих сторін на проекцію на цю сторону іншої сторони.

2) Квадрат будь-якої сторони трикутника, що лежить проти тупого кута, дорівнює сумі квадратів двох інших сторін плюс подвоєний добуток однієї з цих сторін на проекцію на цю сторону другої сторони.

Інакше кажучи, мають місце такі співвідношення:

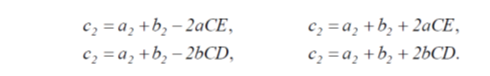
Задачі на доведення

За допомогою теореми косинусів доводять багато інших теорем геометрії. У шкільному підручнику наведено декілька прикладів, зокрема: 1) Cума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін.

2) Нехай a, b, c – сторони трикутника АВС, причому с – найбільша з них. Тоді: якщо с² < a² + b², то кут С – гострий, тобто трикутник гострокутний; якщо с² = a² + b², то кут С – прямий, трикутник АВС – прямокутний. якщо с² > a² + b², то кут С – тупий, трикутник АВС – тупокутний. Нерідко деякі з подібних теорем пропонуються у вигляді задач на доведення.

Друге формулювання теореми синусів

Теорема. У будь-якому трикутнику АВС зі сторонами а, в, с і радіусом описаного кола R мають місце рівності: а = 2RsinA, b = 2RsinB, c = 2RsinC. Інакше кажучи, кожна сторона трикутника дорівнює добутку діаметра описаного кола та синуса протилежного даній стороні кута.

Зокрема, для прямокутного трикутника з гіпотенузою с маємо с = 2 Rsin90° = 2R, тобто гіпотенуза є діаметром описаного кола (і тому центр описаного кола знаходиться на середині гіпотенузи). Для правильного трикутника маємо а = 2Rsin60°– це також часто зустрічається у задачах планіметрії. Теорема містить більше інформації, ніж попереднє формулювання теореми синусів.

Третє формулювання теореми синусів

Іноді зручно сформулювати теорему синусів так, щоб вона не містила тригонометричних функцій. Це дає змогу розв’язувати задачі без використання кутів.

Теорема. У будь-якому трикутнику мають місце співвідношення:

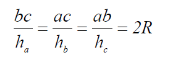
Теоретичний матеріал

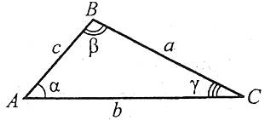
Теорема косинусів. Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.

Наприклад: у , .

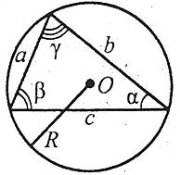
Теорема синусів. У довільному трикутнику відношення будь-якої сторони до синуса протилежного кута стале і дорівнює діаметру описаного навколо нього кола:

Варто пам’ятати, що синуси суміжних кутів рівні, а їх косинуси – протилежні числа:

Розв’язуванням трикутників називається знаходження всіх його шести елементів (тобто трьох сторін і трьох кутів) за будь-якими трьома елементами, що визначають трикутник.

Розглянемо три задачі на розв’язування трикутників. При цьому будемо використовувати такі позначення для сторін трикутника АВС: АВ=с, ВС=а, СА=b.

Задача 1. Дано: а, b, . Знайти: с, , (розв’язування трикутника за двома сторонами і кутом між ними).

Розв’язання:

За теоремою синусів знаходимо с:

Користуючись теоремою косинусів, маємо:

Далі .

Задача 2. Дано: а, , . Знайти: , b, с (розв’язування трикутника за стороною і двома прилеглими кутами).

Розв’язання

За теоремою синусів знаходимо b і с:

Задача 3. Дано а, b, с. Знайти: , , (розв’язування трикутника за трьома сторонами).

Розв’язання:

Користуючись теоремою косинусів, знаходимо: , звідси .

Аналогічно знаходимо . Тоді .

*Основні задачі на обчислення елементів довільних трикутників*
№.	Тип задачі	Дано	Знайти	Алгоритм розв’язання
1.	За стороною і прилеглими до неї кутами	AB, ,	AC, BC,	=, AC=, BC=
2.	За двома сторонами і кутом між ними	AC, AB,	BC, ,	BC=, cos B=, =
3.	За двома сторонами і кутом, протилежним одній із них	AB, BC,	AC, ,	1.sin C = , 2.=, 3. AC=
4.	За трьома сторонами	AC, AB, BC	, ,	1. cos A=, 2. cos B=, 3.=

Прикладні задачі

Прикладна задача – це задача, що виникла зовні математики, але для її розв’язування потрібно використати математичні моделі.

Такі задачі розкривають багатогранність застосування математики в житті.

Розв'язування трикутників застосовують у таких професіях:

у військовій справі (ПВО, точність стрілянини);
у морській, повітряній і космічній навігації;
у сейсмології;
у метеорології;
при розвідці корисних копалин;
при охороні об'єктів;
в медицині;
та ще в багатьох областях.

Застосування в геодезії

Яке б велике будівництво не розпочиналось, першими туди йдуть геодезисти, щоб зняти план місцевості та охарактеризувати рельєф. Коли ж на основі їх матеріалів у проектних організаціях опрацюють проект, геодезисти знову міряють кути, розв'язують трикутники, забивають кілочки - «прив'язують» опрацьований проект до місцевості.

А навіщо вони розв'язують трикутники? Щоб визначити потрібні відстані, не вимірюючи їх безпосередньо. Є ще спеціалісти, які розв'язують подібні задачі в шахтах, тунелях, метро та інших підземних розробках. Це маркшейдери їм також часто доводиться розв'язувати трикутники.

Застосування в навігації

Навігація вирішує питання визначення напрямку і пройденої відстані в морі; методи обчислення шляху і способи визначення місця судна в морі за береговими і плавучими орієнтирами за допомогою штурманських приладів; питання керування і безаварійного проведення судна за особливих умов плавання.

Морехідна астрономія вирішує питання визначення місця судна в морі за положенням небесних світил.

Картографія за допомогою теорії картографічних проекцій, що застосовується в судноводінні, розв'язує аналітичним і графічними способам специфічні штурманські задачі з проведення судна з урахуванням дії різних факторів (вітру, течії і т. д.).

Усі ці науки базуються на строгій математиці. Але конкретні обставини на морі, інколи дуже складні, не завжди дозволяють штурману отримати необхідну інформацію з потрібною точністю навіть за допомогою сучасних технічних засобів. Тому судноводіння, що грунтується на науково-математичній основі, гарантує безпеку судна під час плавання в будь-яких умовах.

Уміння здійснити плавання найзручнішим за даних умов шляхом, найбільш точно провести судно в порт призначення, з необхідною точністю визначити місце судна в морі практично на будь-яких відстанях - усе це залежить від судноводія. І всі задачі розв'язуються із застосуванням знань тригонометрії.

Застосування в астрономії

У давнину за допомогою тригонометрії люди навчилися вимірювати уявні трикутники на небі, вершинами яких були зірки. Зараз тригонометрію застосовують навіть для вимірювання відстані між космічними кораблями.

мост

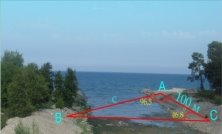
Задача 1. Необхідно побудувати міст через річку з точки А в точку В. Інженер з'ясував, що відстань від точки А до точки С вдалину від берега складає 100 м., а в трикутнику АВС кут А дорівнює 96,5º, а кут З дорівнює 46,8º. Якої довжини буде міст?

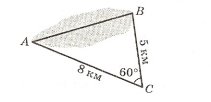
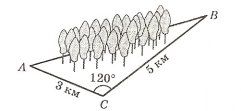
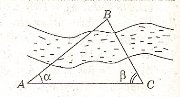
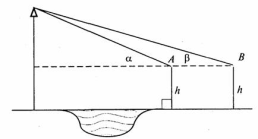
маяк Задача 2. З двох точок А і В, відстань між якими 50 м, вершину гори видно під кутами 50° та 30°. Знайти висоту гори, якщо зріст людини h = 1,64 м.

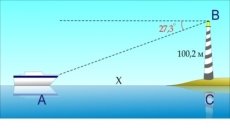
Задача 3. Доглядач маяка, перебуваючи на верхньому поверсі маяка, бачить човен, що терпить лихо, під кутом 27,3º. Висота маяка складає 100,2 км. Як далеко від маяка знаходяться човен?

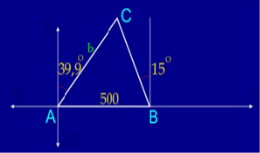Задача 4. Корабель С перебуває у 39,9º на північний схід від корабля А і в 15 º на північний захід від корабля В, який віддалений від А в східному напрямку на 500 м. На якій відстані один від одного знаходиться А і С?

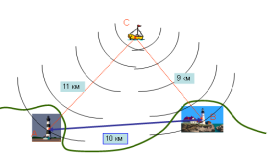Задача 5. Берегові радіомаяки А і В розташовані на відстані 10 км. З судна С з допомогою радіолокаційної станції, що знаходиться на ній, визначені відстані до маяків СА = 11 км і СВ = 9 км. Знайдіть кути САВ і СВА пеленгів радіомаяків.

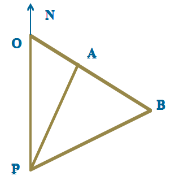
Задача 6. В деякий момент з пароплава Р відмітили азимут пунктів А і В на суші. Азимут пункту А виявився 31°, пункту В - 85°. Напрям АВ по карті - 130°, відстань АВ = 650 м. Знайти відстань від пароплава Р до пункту А в момент вимірювання кутів.

Примітка. Азимут точки А відносно точки Р – це кут, вершина якого знаходиться в точці Р, одна сторона якого РN напрямлена на північ, друга проходить через точку А (за годинниковою стрілкою)

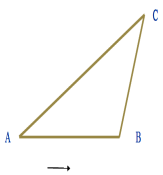
Задача 7. З пароплава в деякий момент видно маяк під кутом в 28° за курсом корабля, а коли пароплав пройшов по курсу 7,8 км, маяк стало видно під кутом в 130° вліво від курсу. Знайти відстань пароплава від маяка в момент, коли був виміряний другий кут.

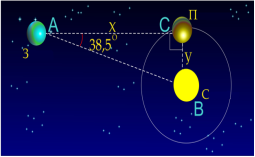Задача 8. Астроном вибрав час, коли Планета перебувала з його точки зору на максимальній відстані від Сонця. Вимірювальний кут між Планетою і Сонцем дорівнює 38,5º. Відомо, що Сонце знаходиться на відстані 148800000км від Землі. Яка відстань від Сонця до Планети?

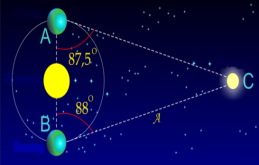Задача 9. Астроном виміряв кут, утворений Сонцем, Землею і Зіркою. Через шість місяців він знову виміряв цей самий кут. Відстань між Сонцем і Землею становить 148800000 км, а виміряні кути відповідно рівні 87,5º і 88º. На якій відстань перебувала Земля і Зірки під час другого вимірювання?

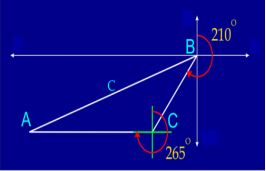Задача 10. Літак летів 20 хвилин у напрямку 210º (вважаючи за годинниковою стрілкою від північного напрямку) зі швидкістю 320 км / год. Потім він змінив курс і на протязі 40 хвилин летів у напрямку 265º. На скільки він віддалився від вихідної точки? Швидкістю вітру можна знехтувати.

Задача 11. Радар засік ворожий літак на відстані 42 км і отримав команду знищити. При розрахунку вийшло, що для потрапляння в літак необхідно запустити ракету під кутом 30º, так як за час польоту ракети літак пролетить 24 км. Скільки пролетить ракета до зіткнення з літаком?

Задача 12. Зі спостережного пункту помічають під кутом 63,5 літак, що пролітає над вежею, висота якої 79,5 м. Пряма, що сполучає спостережний пункт із верхівкою вежі, утворює з горизонтальною площиною кут 2045. На якій висоті знаходиться літак?

Задача 13. Літак летить горизонтально на висоті 8,5 км над рівнем моря зі швидкістю 720 км/год. Пілот замітив, що кут зниження на вершину гори дорівнює 18°. Через 60 с він відмітив, що кут зниження став 81°. Яка висота гори над рівнем моря?

Задача 14. Два літака вилітають одночасно з аеродрому. Швидкість першого літака дорівнює 640 км/год, курс 12°; швидкість другого літака – 500 км/год, курс 178°. Яка відстань буде між ними через 15 хв?

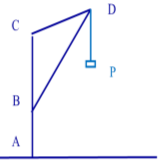Задача 15. На малюнку дана схема підйомного крану, у якого частина стойки ВС = 3,5 м, плече BD = 7,5 м, кут між плечем і стойкою дорівнює 138°. Знайдіть довжину тросу CD і кут ВСD.

Задача 16. В горі прорубали тунель. Вхід А і вхід В знаходяться на одному рівні. Уклін в точці а становить 2,5°, уклін у виході в дорівнює 1,1°. АВ = 85 м. Знайдіть довжину тунелю.

Задача 17. Знайти відстань від острова С, розташованому на озері, до пункту А, що знаходитьсяна березі, якщо відстань АВ=18м, ˂СВА=100˚, ˂САВ=50˚.

Задача 18.Міст через річку між пунктами А і В довжиною 120м видно з пункту С під кутом 46˚ а дорогу між А і С пункту В під кутом 82. Якою повинна бути довжина моста між В і С?

Задача 19. Геодезисту, що знаходиться в пункті С, потрібно виміряти недоступну відстань між опорами А і В, які розділено водоймою, якщо АС=30м, ВС=10м, ˂АСВ=95˚.

Задача 20. М’яч знаходиться в т. А футбольного поля на відстані 23м і 24м від основ В і С стовпів воріт. Знайти кут під яким футболіст спрямовує м’яч до воріт, якщо ширина воріт 7м.

Перевір себе

Запитання:

В чому полягає «розв’язування трикутників»?
Скільки елементів трикутника мають бути відомими, щоб його можна було розв’язувати?
Які теореми потрібно знати, щоб розв’язати трикутник?
Сформулюйте теорему косинусів.
Яку властивість для діагоналей паралелограма можна довести за допомогою теореми косинусів?
Сформулювати теорему синусів.
Сформулювати наслідок з теореми синусів про діаметр кола, описаного навколо трикутника.
Яку властивість бісектриси кута трикутника можна довести за допомогою теореми синусів?
Сформулюйте наслідок про медіани трикутника.
Сформулюйте наслідок про співвідношення між кутами трикутника і протилежними сторонами.
Сформулюйте теорему про суму кутів трикутника.
Скільки типів задач ми розглянули на «розв’язування трикутників»?

Тестові завдання

Тест розрахований на повторення теми «Розв'язування трикутників». Він містить 9 завдань на вибір правильної відповіді. Перші шість завдань по одному балу, три завдання по два бали.

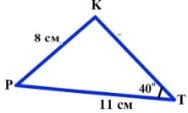Використовуючи рисунок та теорему синусів, укажіть вираз для знаходження синуса кута К.

А) Б) В) Г)

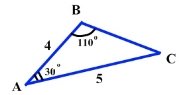2. Використовуючи рисунок та теорему косинусів, укажіть правильне твердження.
А)

Б)

В)

Г)

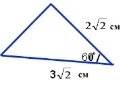3. Використовуючи рисунок знайдіть невідому сторону трикутника.
А) 4см Б) В) Г) 2см

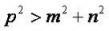Дано трикутник зі сторонами p, m, n. Визначте вид кута, протилежного

до сторони р, якщо

А) тупокутний Б)гострокутний В) прямокутний

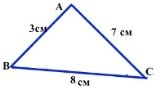Використовуючи рисунок знайдіть косинус кута С.

А) Б) В) Г)

Діагоналі паралелограма дорівнюють 4 см і 10 см, а одна із сторін – 5 см. Знайдіть другу сторону паралелограма.

А)Б)В) Г) 14см

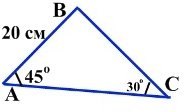
Використовуючи рисунок знайдіть сторону ВС.

А)

Б)

В) 15см

Г) 20см

Знайдіть радіус кола, описаного навколо трикутника зі стороною 18 см і протилежним до неї кутом 120º.

А)Б)В)Г) 18см

Знайдіть меншу діагональ паралелограма зі сторонами, що дорівнюють 8 см і 15 см, і гострим кутом 60º.

А) Б) В) 13см Г) 14см

Вставити пропущені слова:

У трикутнику проти … лежить більший кут, проти більшого кута лежить … ( більшої сторони; більша сторона).
Сторони трикутника пропорційні синусам … кутів. (протилежних)
Кожне з відношень дорівнює... (діаметру кола, описаного навколо цього трикутника)
Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без... (подвоєного добутку цих сторін на косинус кута між ними)
Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін «±» подвоєний добуток однієї з них на проекцію другої. Знак «+» беремо тоді, коли протилежний кут …, а знак «-», коли …( тупий; гострий).
Теорему косинусів називають іноді узагальненою теоремою …(Піфагора).
Розв’язати трикутник означає: за даними … основними елементами трикутника … . При цьому серед заданих основних елементів хоча б один повинен бути … (трьома; знайти три інші його основні елементи; стороною трикутника).
Які теореми потрібно знати, щоб розв’язати трикутник? ( теорему синусів, теорема косинусів)

Ознайомившись з історичною довідкою і дайте відповіді на запитання:

В якому столітті видатним астрологом ал-Беруні була доведена теорема синусів? (у XI)
Коли нею почали користуватися європейські математики? (у XVI столітті)
Яка теорема була доведена геометрично в «Началах» Евкліда? (теорема косинусів)
Ким і коли вона була сформульована словесно? (французьким математиком Франсуа Вієтом, XVI століття)
Хто і коли надав їй сучасного вигляду? (французький математик Лазар Карно, у 1801 році)

Математичний диктант 1

Якщо в трикутнику відомі дві сторони в і с та кут між ними, то третя сторона дорівнює ...
Якщо в трикутнику відомі сторона а та два прилеглі до неї кути β і γ, то дві інші сторони можна знайти так ...
Якщо в трикутнику відомі дві сторони в і с та проекція однієї з них на другу, то третя сторона дорівнює ...
Сума квадратів діагоналей паралелограма дорівнює ...
У трикутнику проти більшої сторони лежить ...
У трикутнику проти меншого кута лежить ...
Який кут трикутника найбільший, якщо його сторона а = 7, в = 9, с = 5?
Який вид трикутника, якщо а:в:с = 9:6:10 ?
Трикутник зі сторонами 3 см, 4 см, 5 см ...

Математичний диктант 2

Якщо в трикутнику відомі дві сторони bі с та кут між ними, то третя сторона дорівнює...
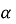
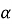
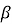
Якщо в трикутнику відомі сторона c та два прилеглі до неї кути і , то дві інші сторони можна знайти так...
Якщо в трикутнику відомі сторони а, bі с, то косинус кута дорівнює
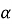
Якщо в трикутнику відомі сторони а, bі с, то кут, протилежний стороні с гострий, якщо…
Якщо в трикутнику відомі сторони а, bі с, то кут, протилежний стороні с тупий, якщо…
Сума квадратів діагоналей паралелограма дорівнює...
У трикутнику проти більшої сторони лежить...
У трикутнику проти меншого кута лежить...
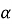
Якщо в трикутнику відома сторона а і протилежний кут , то радіус описаного навколо трикутника кола, дорівнює…

Графічний диктант «Так чи ні?»

Учні креслять трикутник з вершиною вгору, якщо твердження правильне і вершиною вниз, якщо неправильне.

Теорема синусів справедлива для будь-якого трикутника.
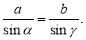
За теоремою косинусів можна знайти невідому сторону трикутника, якщо відомі його сторона і два кути.
За трьома сторонами можна розв’язати трикутник.
с²=а²+в²-2авcos.
У трикутнику проти більшого кута лежить менша сторона.
За трьома кутами можна розв’язати трикутник.
Медіани трикутника діляться точкою їх перетину у відношенні 1:2, починаючи від вершини.
Відношення сторони до синуса протилежного кута дорівнює діаметру кола, описаного навколо цього трикутника.
Якщо відомо 2 кути трикутника, то третій кут можна знайти за допомогою теореми про суму кутів трикутника.

1 варіант	2 варіант
Знайдіть відстань між недоступними точками А і В за даними рисунка:
$C:\Documents and Settings\Кузенька\Мои документы\Мои результаты сканировани\2010-10 (окт)\Копия сканирование0006.jpg$	$C:\Documents and Settings\Кузенька\Мои документы\Мои результаты сканировани\2010-10 (окт)\сканирование0006.jpg$
Поясніть як знайти відстань від точки А до недоступної точки В $C:\Documents and Settings\Кузенька\Мои документы\Мои результаты сканировани\2010-10 (окт)\сканирование0001.jpg$
Якщо АС=12,	Якщо АС=15,

Завдання за готовими рисунками

Список використаної літератури

Державний стандарт базової і повної загальної середньої освіти / [Електронний ресурс] – Режим доступу: http://www.mon.gov.ua/index.php/ua
Боровик. Г. В. Компетентнісний підхід до навчання учнів на уроках математики Методичний посібник для вчителів.
Пометун О. Компетентнісний підхід – найважливіший орієнтир розвитку сучасної освіти // Рідна школа. – 2005. - № 1. – С. 29-31.
Метод проектів – http://iteach.com.ua/resources/full-time-tuition/m1
К. Малашенко. Технологія проектного навчання./Завуч, травень,2006р.
Мерзляк А. Г. Геометрія : підруч. для 9 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. — Х. : Гімназія, 2017. — 240 с.
Інтернет ресурси.